\(\dfrac{1}{x}+\dfrac{1}{y}=1\).
The main objective of this question is to explicitly write the given function in terms of $x$ and to express $y’$ by using explicit differentiation.
An algebraic function in which the output variable, say a dependent variable, can be expressed explicitly in terms of the input variable, say an independent variable. This function typically has two variables that are dependent and independent variables. Mathematically, let $y$ be the dependent variable and $x$ be the independent variable, then $y=f(x)$ is said to be an explicit function.
Taking the derivative of an explicit function is referred to as explicit differentiation. The derivative of an explicit function is computed similarly to the differentiation of algebraic functions. The differentiation of the explicit function $y=f(x)$ can be expressed as $\dfrac{dy}{dx}=\dfrac{df(x)}{dx}$ or $y’=f'(x)$. Moreover, simple differentiation rules are applied to find the derivative of an explicit function.
Expert Answer
Given function is:
$\dfrac{1}{x}+\dfrac{1}{y}=1$
First, write $y$ in terms of $x$ as:
$\dfrac{1}{y}=1-\dfrac{1}{x}$
$\dfrac{1}{y}=\dfrac{x-1}{x}$
Inverting both sides:
$y=\dfrac{x}{x-1}$ (1)
Now, differentiate (1) with respect to $x$ to obtain $y’$:
$\dfrac{dy}{dx}=\dfrac{d}{dx}\left(\dfrac{x}{x-1}\right)$
Apply the quotient rule on right hand side of the above equation:
$y’=\dfrac{(x-1)\cdot \dfrac{dx}{dx}-x\cdot \dfrac{d(x-1)}{dx}}{(x-1)^2}$
$y’=\dfrac{(x-1)\cdot 1-x\cdot 1}{(x-1)^2}$
$y’=\dfrac{x-1-x}{(x-1)^2}$
$y’=\dfrac{-1}{(x-1)^2}$
Example 1
Write $4y-xy=x^2+\cos x$ explicitly in terms of $x$. Also, find $y’$.
Solution
The explicit representation of the given function is:
$(4-x)y=x^2+\cos x$
$y=\dfrac{x^2+\cos x}{(4-x)}$
Now, to find $y’$, differentiate both sides of the above equation with respect to $x$:
$\dfrac{dy}{dx}=\dfrac{d}{dx}\left(\dfrac{x^2+\cos x}{4-x}\right)$
Use quotient rule on right hand side:
$y’=\dfrac{(4-x)\cdot (2x-\sin x)+(x^2+\cos x)\cdot (-1)}{(4-x)^2}$
$y’=\dfrac{8x-2x^2+x\sin x-x^2-\cos x}{(4-x)^2}$
$y’=\dfrac{-3x^2+(8+\sin x)x-\cos x}{(4-x)^2}$
Example 2
Write $\dfrac{x^3}{y}=1$ explicitly in terms of $x$. Also, find $y’$.
Solution
The given equation can be explicitly written as:
$y=x^3$
To find $y’$, differentiate both sides of the above equation using power rule:
$\dfrac{dy}{dx}=\dfrac{d}{dx}(x^3)$
$y’=3x^2$
Example 3
Given $3x^3-5x^2-y=x^6$. Explicitly write $y$ in terms of $x$ to find $y’$.
Solution
We can write the given equation explicitly as:
$-y=x^6-3x^3+5x^2$
$y=-x^6+3x^3-5x^2$
Now, differentiate above equation using power rule:
$\dfrac{dy}{dx}=\dfrac{d}{dx}(-x^6+3x^3-5x^2)$
$y’=-6x^5+9x^2-10x$
$y’=-x(6x^4-9x^2+10)$
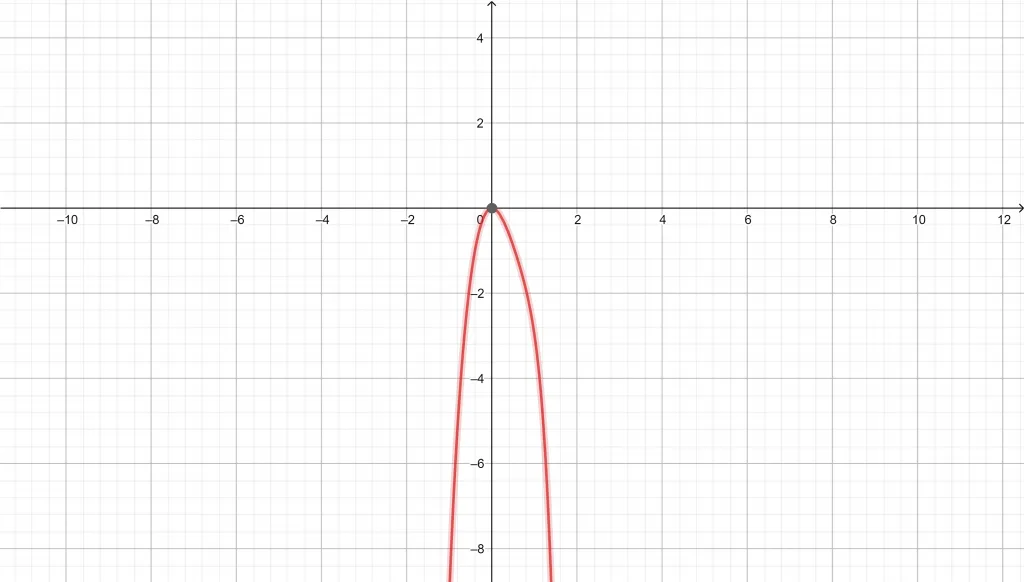
Graph of $y=-x^6+3x^3-5x^2$
Images/mathematical drawings are created with GeoGebra.
