
This question aims to find the next number in the series of the given numbers. Number series is a sequential arrangement of numbers following a certain defined pattern.
Different types of number series
The most common pattern in the number series are the following:
- Series consisting of perfect squares
A series based on perfect squares is mostly based on perfect squares of numbers in a certain order, and generally, one of the numbers in this type of series is missing.
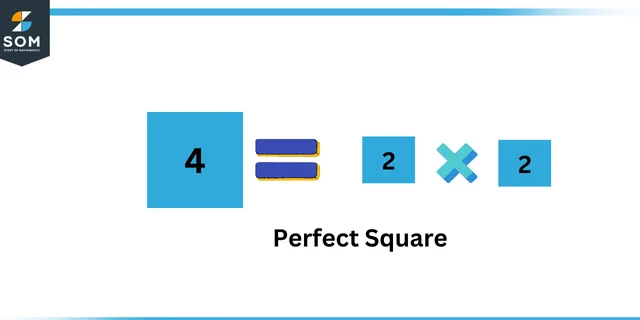
Perfect square
Example: $4, 9, 16, 25,?$
Sol: $4 = 2^{2}, 9 = 3^{2}, 16 = 4^{2}, 25 = 5^{2}, 36 = 6^{2}$
- Perfect cubes series
It is based on a number of dice in a certain order, and one of the numbers in the row is missing.
Example: $27, 125, 343,?$
Sol: $3^{3}, 5^{3}, 7^{3}, 9^{3}$
- Geometric series
Geometric series is based on either descending or ascending order of the numbers and each subsequent number is obtained by dividing or multiplying previous number by a specific number.
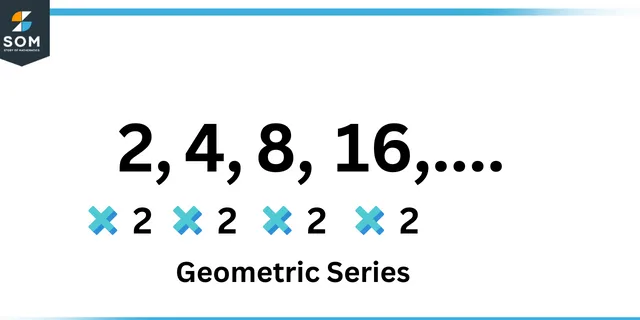
Geometric series
Example: $4, 36, 324, 2916?$
Sol: $4 \times 9 = 36, 36 \times 9 = 324, 324 \times 9 = 2916, 2916 \times 9 = 26244$.
- Arithmetic series
It consists of a series in which next term is obtained by adding/subtracting a constant number from the previous term. Example: $-3,4,11,18$ where the number to be added to get the new number is $5$.

Sum of arithmetic series
- Two-stage type series
In a two-step arithmetic series, differences of consecutive numbers form an arithmetic series.
Example: $2, 4, 7, 11..$
Sol: $4 – 2 = 2, 7 – 4 = 3, 11 – 7 = 4$
Now, the arithmetic sequence $2, 3, 4$
So $5$ is added to the last number given, so the answer is $11 + 5 = 16$
Expert Answer
The next number in the series is $20$.
Given series is $38,36,30,28,22$.
Seeing alternative numbers, there are two series.
First series is $38,30,22$.
The common difference between the two consecutive numbers is:
\[30-38=22-30=-8\]
Second series is $36,28$.
The common difference between the two consecutive numbers is:
\[28-36=-8\]
Therefore, the next number is
\[28-8=20\]
The next number is $20$.
Numerical Result
The next number in the series of the numbers $38,36,30,28,22$ is $20$.
Example
What is next number in the series $1,4,9,16,25$?
Solution
Given series is $1,4,9,16,25$.
First number: $1=1^{2}$
Second number: $4=2^{2}$
Third number: $9=3^{2}$
Forth number: $16=4^{2}$
Fifth number: $25=5^{2}$
The series of the numbers is $1,2,3,4,5$. The next number is $6$.
Therefore,
The next number is $6^{2}=36$.
The complete series is $1,4,9,16,25,36$.
