Vertical Angles Theorem – Definition, Applications, and Examples

The vertical angles theorem focuses on the angle measures of vertical angles and highlights how each pair of vertical angles share the same measure. Through the vertical angles theorem, we can now solve problems and find unknown measures when vertical angles are involved.

The vertical angles theorem establishes the relationship between two vertical angles. Through this theorem, we can equate the measures of two vertical angles when solving problems involving vertical angles.

This is why it’s time for us to break down the vertical angles theorem, understand its proof, and learn how to apply the theorem to solve problems.

What Is the Vertical Angles Theorem?

The vertical angles theorem is a theorem that states that when two lines intersect and form vertically opposite angles, each pair of vertical angles has the same angle measures. Suppose that lines $l_1$ and $l_2$ are two intersecting lines that form four angles: $\{\angle 1, \angle 2, \angle 3, \angle 4\}$.

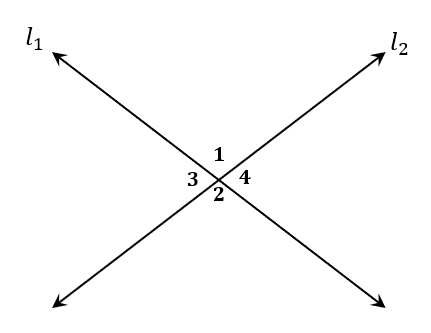
Recall that vertical angles are angles that are facing opposite each other when two lines intersect. This means $l_1$ and $l_2$ form the following pairs of vertical angles:

\begin{aligned}\textbf{Vertic}&\textbf{al Angles}\\\\\angle 1 &\text{ and } \angle 2\\\angle 3 &\text{ and } \angle 4\end{aligned}

According to the vertical angles theorem, each pair of vertical angles will share the same angle measures. 

Meaning, we have the following relationship:

\begin{aligned}\textbf{Vertical An}&\textbf{gles Theorem}\\\\\angle 1 &= \angle 2\\\angle 3 &= \angle 4\end{aligned}

This theorem leads to a wide range of applications – we can now find the measures of unknown angles given they meet the conditions for the vertical angles theorem. We can also solve problems involving vertical angles thanks to the vertical angles theorem.

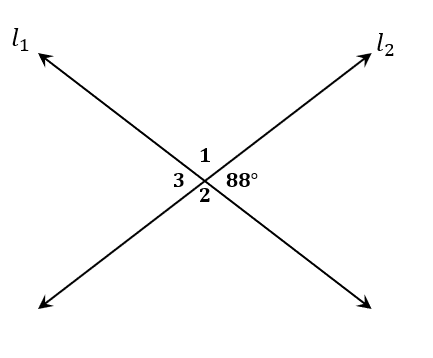Take a look at the image shown above – suppose that one angle measure is given to be $88^{\circ}$. Use geometric properties and the vertical angle theorem to find the measures of the three remaining vertical angles.

• The angle measuring $88^{\circ}$ and $\angle 2$ form a linear pair, so their sum is equal to $180^{\circ}$.

\begin{aligned}\angle 2 + 88^{\circ} &= 180^{\circ}\\\angle 2&= 180^{\circ}- 88^{\circ}\\&= 92^{\circ}\end{aligned}

• The angle measuring $88^{\circ}$ and $\angle 3$ are vertical angles, so they share the same measures.

\begin{aligned}\angle 3 &= 88^{\circ}\end{aligned}

• Similarly, since $\angle 2$ and $\angle 1$ are vertical angles, their angle measures are equal.

\begin{aligned}\angle 1 &= \angle 2\\&= 92^{\circ}\end{aligned}

This is an example of how, through the vertical angles theorem, it is now possible to solve similar problems and find unknown measures of angles formed by intersecting lines. We’ve prepared more examples for you to work on, but for now, let’s break down how this theorem has been formed.

How To Prove Vertical Angles Are Congruent?

When proving that vertical angles will always be congruent, use algebraic properties and the fact that the angles forming a line add up to $180^{\circ}$. When two lines intersect each other, it is possible to prove that the vertical angles formed will always be congruent.

• Locate the vertical angles and identify which pair share the same angle measures.
• Relate the linear pair and set up an equation showing that their sum is equal to $180^{\circ}$.
• Use the equations to prove that each pair of vertical angles are equal.

Let’s go back to the intersecting lines and angles shown in the first section. The following pairs of angles are linear pairs (visually, these are angles that form a line). This means that the sum of their angles is equal to $180^{\circ}$.

\begin{aligned}\angle 1+ \angle 4= 180^{\circ}\,\,(1)&,\,\,\,\angle 1+ \angle 3= 180^{\circ}\,\,(2)\\\angle 2+ \angle 4= 180^{\circ}\,\,(3)&,\,\,\,\angle 2+ \angle 3= 180^{\circ}\,\,(4)\end{aligned}

Working on the first two equations, isolate $\angle 1$ on the left-hand side of each of the equations.

\begin{aligned}\angle 1+ \angle 4 &= 180^{\circ}\\\angle 1&= 180^{\circ} – \angle 4\\\angle 1+ \angle 3&= 180^{\circ}\\\angle 1&= 180^{\circ} – \angle 3\end{aligned}

By transitive property, the two resulting expressions, $(180^{\circ} – \angle 4)$ and $(180^{\circ} – \angle 3)$, are equal.

\begin{aligned}180^{\circ} – \angle 4&= 180^{\circ} – \angle 3\\ -\angle 4&= -\angle 3\\ \angle 3&= \angle 4\end{aligned}

Now, try to work with equations (1) and (3) and show that $\angle 1$ is also equal to $\angle 2$.

Since both angles $\angle 1$ and $\angle 2$ are each equal to $(180 – \angle 4)$, by transitive property, the two angles are equal.

\begin{aligned}\angle 1&= 180^{\circ} – \angle 4\\ \angle 2&= 180^{\circ} – \angle 4\\\therefore\angle 1&= \angle 2\end{aligned}

This proof has confirmed that $\angle 1 = \angle 2$ and $\angle 3 = \angle 4$. Hence, we’ve proven that the vertical angles theorem is true: the measures of two vertical angles are the same.

Try out more problems involving vertical angles to master this theorem. Head over to the next section when you’re ready! 

Example 1

The lines $m$ and $n$ intersect each other and form the four angles as shown below. Using the vertical angles theorem, what are the values of $x$ and $y$?

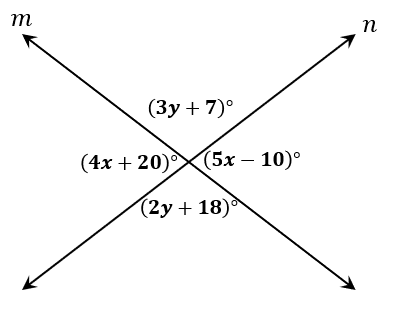
Solution

The intersecting lines $m$ and $n$ form two pairs of vertical angles: $(4x +20)^{\circ}$ and $(5x – 10)^{\circ}$ as well as $(3y +40)^{\circ}$ and $(2y +70)^{\circ}$. According to the vertical angles theorem, the vertical angles’ measures are equal.

To find the values of $x$ and $y$, equate the expressions for each pair of vertical angles. Solve for $x$ and $y$ from the two resulting equations.

Hence, we have the following values for $x$ and $y$: $x = 30$ and $y = 7$.

Example 2

The lines $l_1$ and $l_2$ intersect each other and form the four angles as shown below. Using the vertical angles theorem, what are the values of $x$ and $y$?

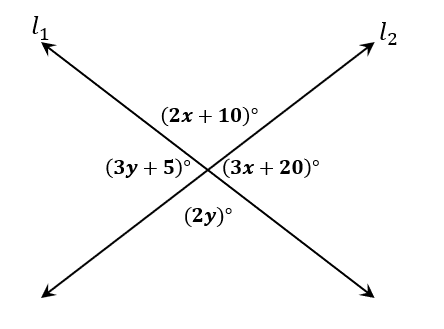
Solution

Similar to the previous example, the lines $l_1$ and $l_2$ form the following pairs of angles:

• The angles $(2x +10)^{\circ}$ and $(3x +20)^{\circ}$ are linear pair of angles.
• Similarly, $(3y + 5)^{\circ}$ and $(2y)^{\circ}$ form a line, so their angles are supplementary.
• The following are pairs of vertical angles and are equal: $(2x + 10)^{\circ} = (2y)^{\circ}$ and $(3y + 5)^{\circ} = (3x + 20)^{\circ}$.

Seeing that each pair of vertical angles are in terms of $x$ and $y$ each, find the value of either variable first by using one of the linear pairs of angles.

\begin{aligned}(2x +10)^{\circ} + (3x +20)^{\circ} &= 180^{\circ}\\5x + 30 &= 180\\5x&= 150\\x&= 30\end{aligned}

Use $x = 30$ to find the measure of $(2x + 10)^{\circ}$.

\begin{aligned}(2x +10)^{\circ} &= 2(30) + 10\\&= 70\end{aligned}

Through the vertical angles theorem, we know that this angle is equal to the measure of $(2y)^{\circ}$. Equate the value of $(2x + 10)^{\circ}$ to $(2y)^{\circ}$ to solve for $y$.

\begin{aligned}(2x +10)^{\circ} &= (2y)^{\circ}\\70^{\circ} &= (2y)^{\circ}\\y&= 35\end{aligned}

This means that $x = 30$ and $y = 35$.

Practice Questions

1. The lines $m$ and $n$ intersect each other and form the four angles as shown below. Using the vertical angles theorem, what is the value of $x + y$?

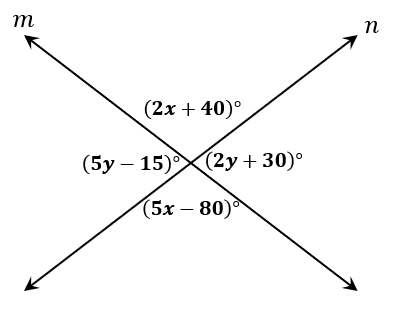
A. $x + y= 25$
B. $x + y= 35$
C. $x + y= 45$
D. $x + y= 55$

2. The lines $l_1$ and $l_2$ intersect each other and form the four angles as shown below. Using the vertical angles theorem, what is the value of $x – y$?

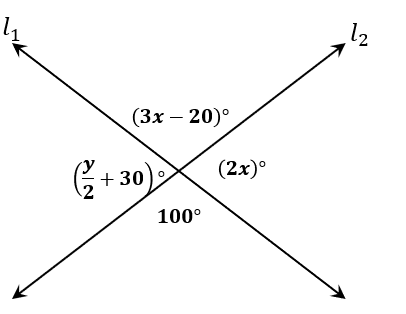
A. $x – y= 30$
B. $x – y= 40$
C. $x – y= 60$
D. $x – y= 80$

3. Suppose that angles $\angle AOB$ and $\angle COD$ are vertical angles and are complementary to each other. What is the value of $\angle AOB$?

A. $\angle AOB = 30^{\circ}$
B. $\angle AOB = 45^{\circ}$
C. $\angle AOB = 90^{\circ}$
D. Vertical angles can never be complementary.

Answer Key

1. D
2. C
3. B