• Home
  • >
  • y = x Reflection – Definition, Process and Examples

y = x Reflection – Definition, Process and Examples

The $\boldsymbol{ y = x}$ reflection is simply “flipping” a shape or a point over a diagonal line. Since $ y= x$ reflection is a special type of reflection, it can also be classified as a rigid transformation. Knowing how to reflect over the line $y=x$ will come in handy when graphing functions and predicting the graph of inverse functions.

The $\boldsymbol{ y = x}$ reflection projects the pre-image over the diagonal line that passes through the origin and represents $\boldsymbol{ y = x}$. This results in switching the places of the x and y coordinates on the coordinate system.

This article focuses on a special type of reflection: over the line $y = x$. It explores the fundamentals of reflecting different types of pre-images. By the end of the discussion, try out different examples and practice questions to further master this topic!

How To Reflect y = x?

To reflect a point or object over the line $y=x$, switch the values of $x$ to $y$ and values of $y$ to $x$. This process applies even for functions – meaning, to reflect a function over $y = x$, switch the input and output values. When given the shape graphed on the $xy$-plane, switch the $x$ and $y$ coordinates to find the resulting image.

The best way to master the process of reflecting the line, $y = x$, is by working out different examples and situations. Apply what has been discussed to reflect $\Delta ABC$ with respect to the line $y = x$.

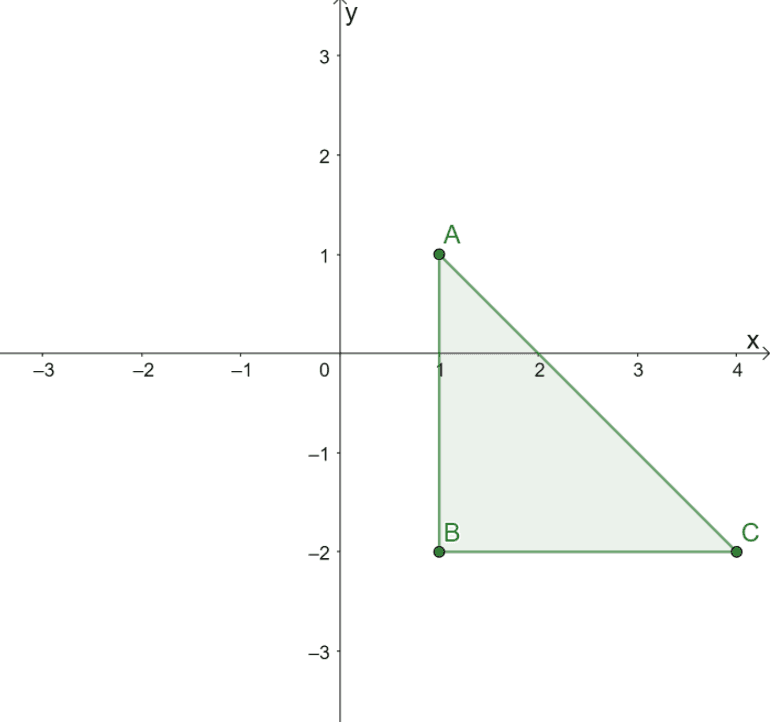
how to reflect the triangle over y

The triangle shown above has the following vertices: $A = (1, 1)$, $B = (1, -2)$, and $C = (4, -2)$. To reflect $\Delta ABC$ over the line $y = x$, switch the $x$ and $y$ coordinates of all three vertices.

\begin{aligned}A \rightarrow A^{\prime} &: \,\,\,\,\,({\color{Teal}1}, {\color{DarkOrange} 1}) \rightarrow ({\color{DarkOrange}1}, {\color{Teal} 1})\phantom{x}\\B \rightarrow B^{\prime} &: ({\color{Teal}1}, {\color{DarkOrange} -2}) \rightarrow ({\color{DarkOrange}-2}, {\color{Teal} 1})\\C \rightarrow C^{\prime} &: ({\color{Teal}4}, {\color{DarkOrange} -2}) \rightarrow ({\color{DarkOrange}-2}, {\color{Teal} 4})\end{aligned}

Plot these three points then connect them to form the image of $\Delta A^{\prime}B^{\prime}C^{\prime}$. Construct the line of reflection as a guide and double-check whether the reflection was performed correctly.

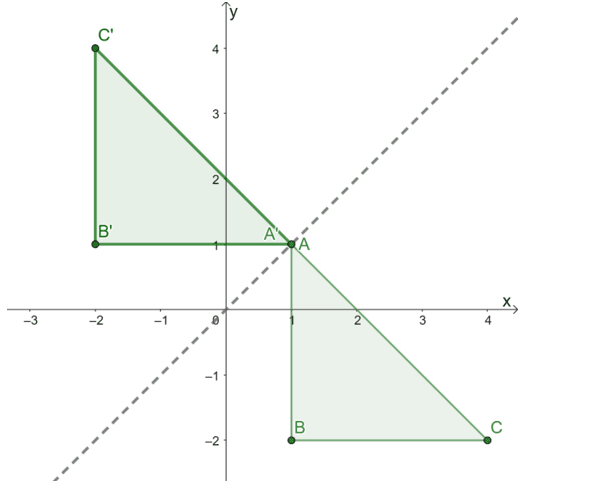
resulting image of a triangle after being reflected over

The resulting image is as shown above. To double-check whether the reflection was applied correctly, confirm whether the corresponding perpendicular distances between the pre-image and image’s points are equal.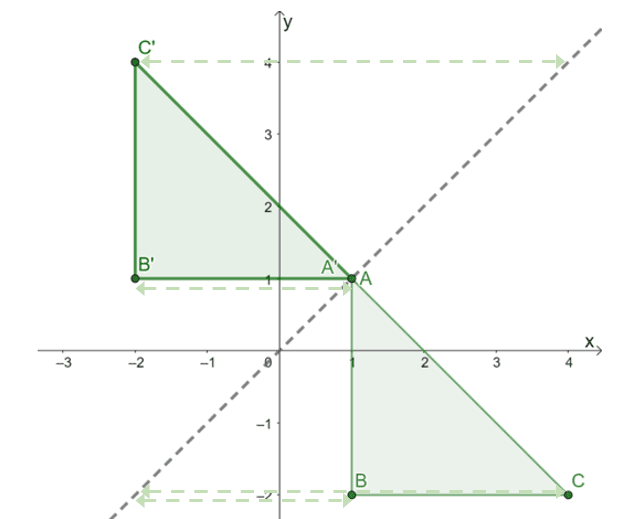double checking the resulting image of a triangle after being reflected over y

This confirms that the result of reflecting $\Delta ABC$ over the line of reflection $y = x$ is triangle $\Delta A^{\prime}B^{\prime}C^{\prime}$ with the following vertices: $A^{\prime} =(1, 1)$, $B^{\prime} = (-2, 1)$, and $C^{\prime} = (-2, 4)$.

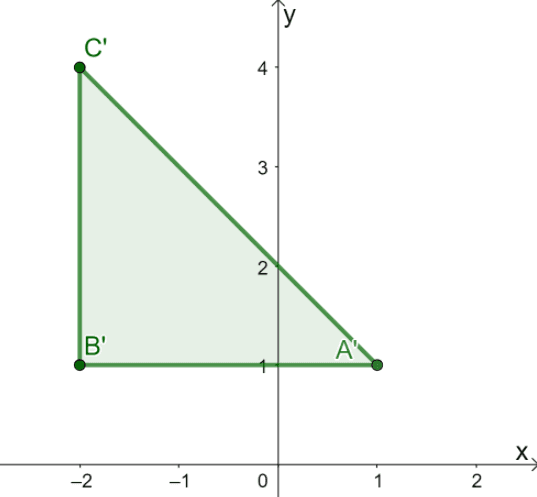
reflecting a triangle over y

Apply a similar process when asked to reflect functions or shapes over the line of reflection $y = x$.

y = x Reflection: What Is It?

The $y = x$ reflection is a type of reflection on the Cartesian plane where the pre-image is reflected with respect to the line of reflection with an equation of $y = x$. Imagine a diagonal line passing through the origin, $y = x$ reflection occurs when a point or a given object is reflected over this line.

Before diving deeper into the process of the $y = x$ reflection, recall how this equation is represented on the $xy$-plane. The points $(-1, 1)$, $(0, 0)$, and $(1, 1)$ pass through the lines of $y = x$, so use these to graph the line of reflection.

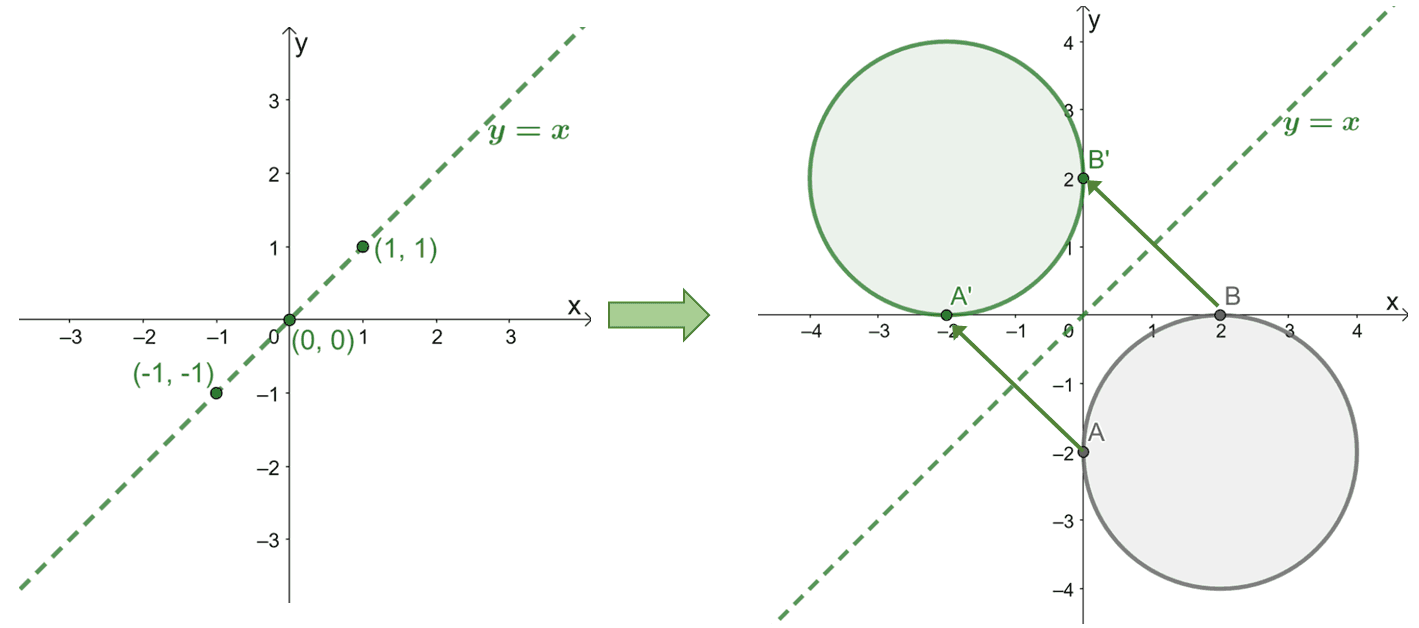
line of reflection over

Throughout this discussion, the focus will be on reflecting points and polygons of different shapes over the line $y = x$. Take a look at the graphs shown above — the circle is reflected over the line of reflection $y = x$.

Now, take a closer look at the points to see how the reflection over $y = x$ affects them:

\begin{aligned}A =(0, -2) &\rightarrow A^{\prime} = (-2, 0)\\B=(2, 0) &\rightarrow B^{\prime} = (0, 2)\end{aligned}

The coordinates of the pre-image and image have switched places. This is, in fact, what makes the $y = x$ reflection special. When projected onto the line of reflection, the $\boldsymbol{x}$ and $\boldsymbol{y}$ coordinate of the points switch their places.

\begin{aligned}\color{Teal} \textbf{Reflect} &\color{Teal}\textbf{ion of } \boldsymbol{y = x}\\(x, y) &\rightarrow (y, x)\end{aligned}

This time, shift the focus from the points towards the resulting image of the circle after being reflected over $y = x$.

  • The pre-image is a circle with radius of $2$, center at $(2, -2)$, and an equation of $(x – 2)^2 + (y +2)^2 = 4$.
  • The image is a circle with radius of $2$, center at $(-2, 2)$, and an equation of $(y – 2)^2 + (x +2)^2 = 4$.

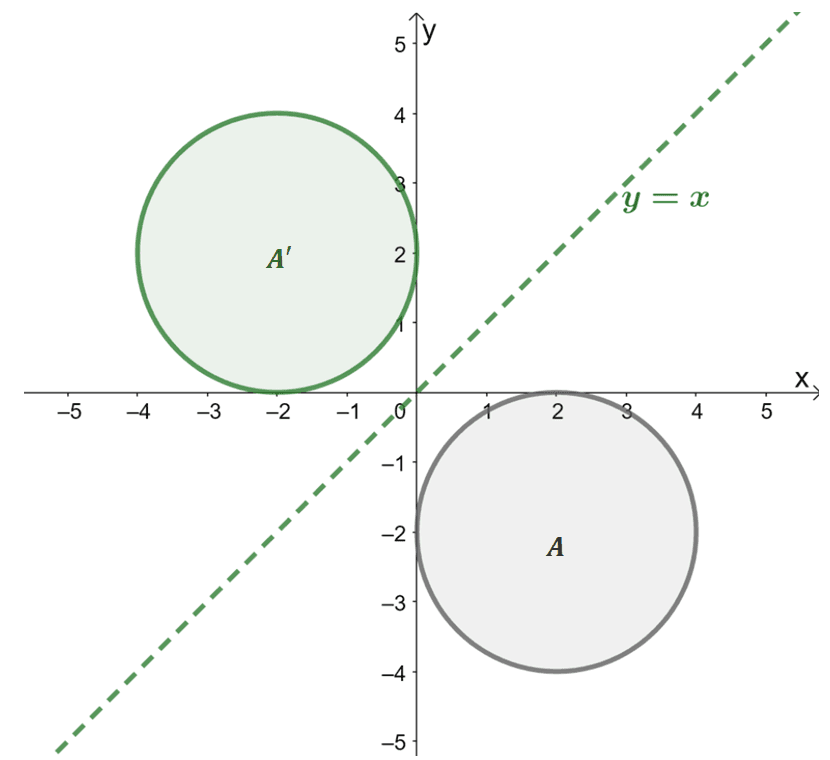
reflection over y x of a function

Remember that the inverse function’s shape is the result of reflecting the function over the line $y = x$. Apply the same process when finding the function of the transformed image: switch the places of the variables to find the image’s function.

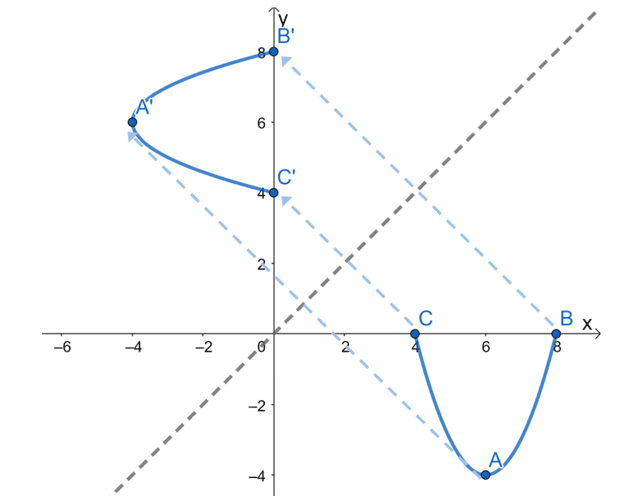
y x reflection of a parabola

The function $y = (x -6)^2 -4$ has a parabola as its curve. When reflected over the line $y =x$, the $x$ and $y$ coordinates of all the points lying along the curve will switch their places. This also means that the function’s input and output variable will have to switch places.

\begin{aligned}y &= (x – 6)^2 – 4\\ &\downarrow \\ x &= (y- 6)^2 -4\end{aligned}

Now, observe the transformation of $\Delta ABC$ over the line $y =x$ and try to find interesting properties of the transformation.

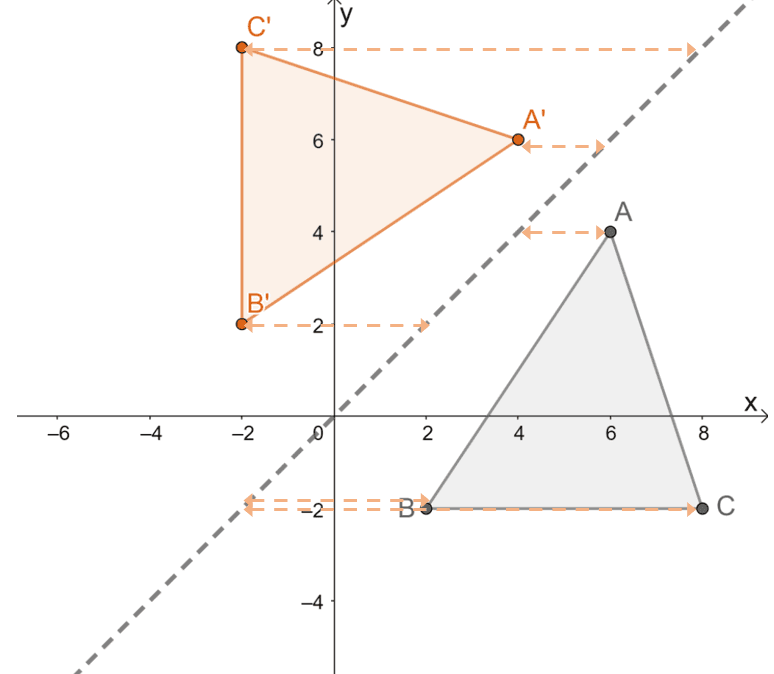
properties of reflection over y

Here are other important properties to remember when reflecting objects over the line of reflection $y = x$.

  1. The perpendicular distance between the pre-image’s point and the corresponding image’s point is equal.
  2. The reflected image retains the shape and size of the pre-image, so $y = x$ reflection is a rigid transformation.
The section below offers more examples to make sure that by the end of this discussion, reflecting over the line $y = x$ is going to feel easy and simple!

Example 1

Graph the three points $(-1, 4)$, $(2, 3)$, and $(-4, -2)$ on the $xy$-plane. Determine the resulting points when each of these points are reflected over the line of reflection $y =x$. Graph these resulting points as well and use the graph to double-check the three images.

Solution

Plot each of the three given points on the Cartesian plane. The graph below shows the position of all three points in one coordinate plane.

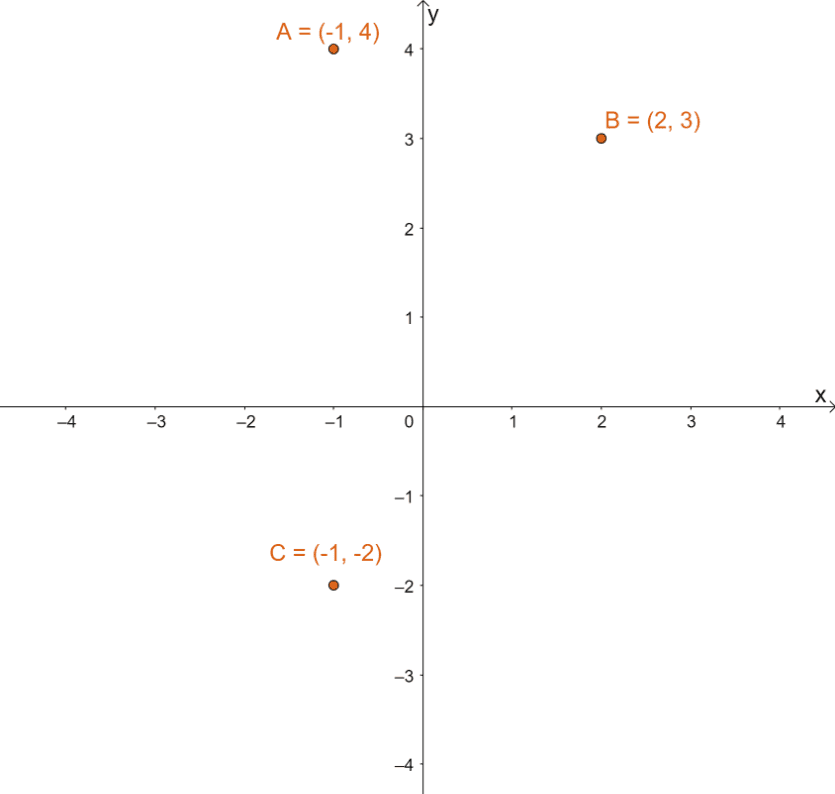
graphing three points or pre images

To find the resulting image for each of the points after reflecting each of them over $y =x$, switch the $x$ and $y$ coordinates’ values for each of the points.

\begin{aligned}A \rightarrow A^{\prime} &:\,\,\,\,({\color{Teal}-1}, {\color{DarkOrange} 4}) \rightarrow ({\color{DarkOrange}4}, {\color{Teal} -1})\phantom{x}\\B \rightarrow B^{\prime} &: \,\,\,\,\,\,\,\,({\color{Teal}2}, {\color{DarkOrange} 3}) \rightarrow ({\color{DarkOrange}3}, {\color{Teal} 2})\\C \rightarrow C^{\prime} &: ({\color{Teal}-1}, {\color{DarkOrange} -2}) \rightarrow ({\color{DarkOrange}-2}, {\color{Teal} -1})\end{aligned}

Plot these new sets of points on the same $xy$-plane. Graph the line of reflection $y =x$ as well to help answer the follow-up question.

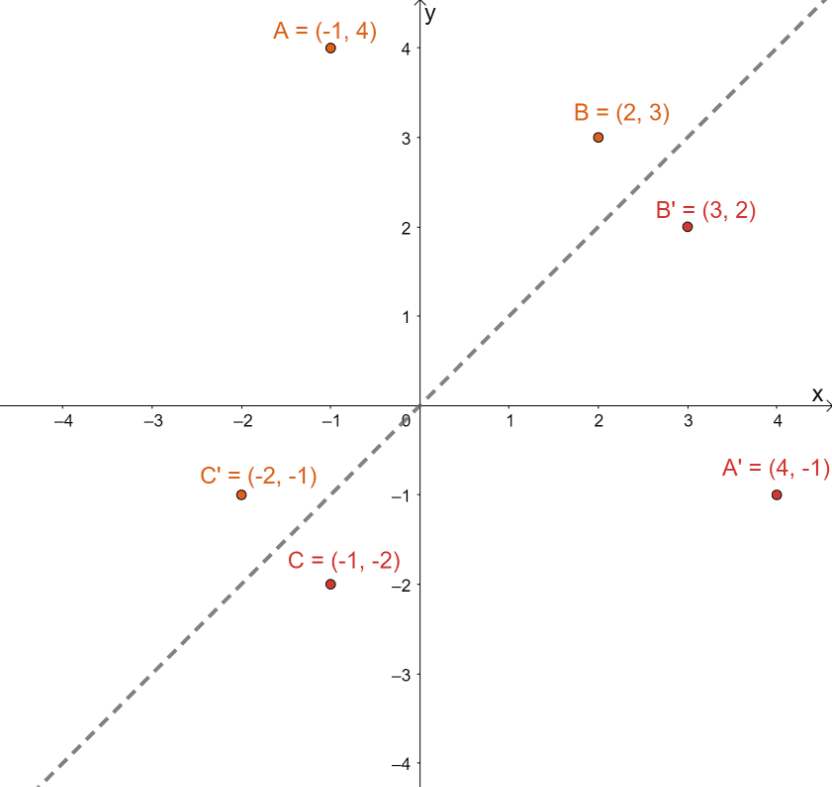
reflecting points over the line of reflection y

To confirm if the projected images are in the right position, determine the perpendicular distances between the corresponding images and pre-images: $A \rightarrow A^{\prime}$, $B \rightarrow B^{\prime}$, and $C \rightarrow C^{\prime}$.

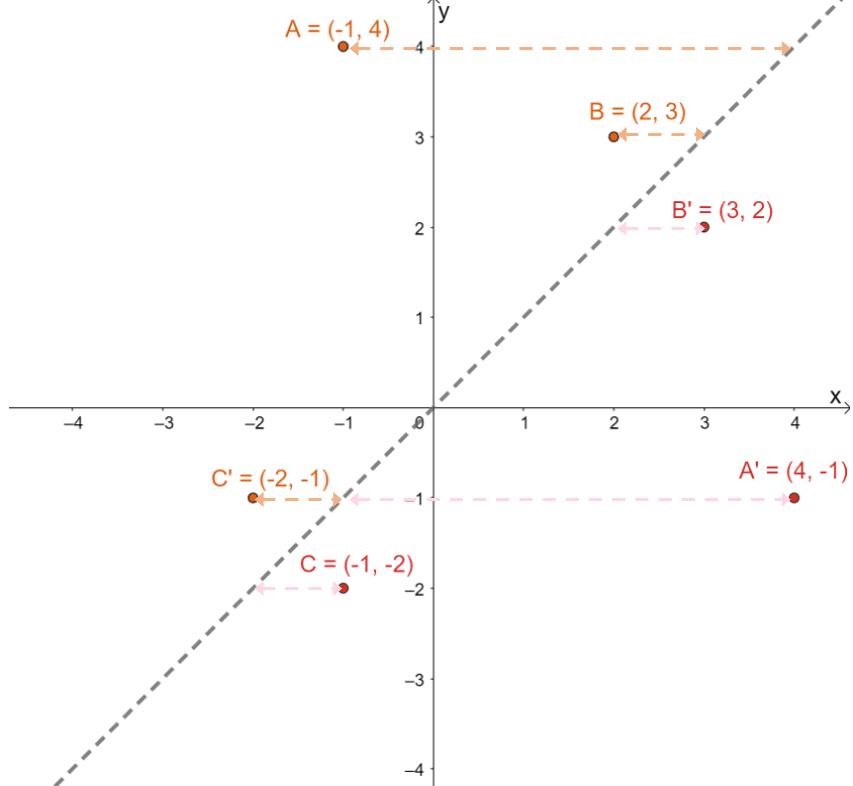
confirming the image and preimage over the line y

Example 2

The square $ABCD$ has the following vertices: $A=(-3, 3)$, $B=(-3, 1)$, $C=(-1, 1)$, and $D=(-1, 3)$. When the square is reflected over the line of reflection $y = x$, what are the vertices of the new square?

Graph the pre-image and the resulting image on the same Cartesian plane.

Solution

When reflected over the line of reflection $y = x$, find the image’s vertices by switching the places of the $x$ and $y$ coordinates of the pre-image’s vertices.

 \begin{aligned}A \rightarrow A^{\prime} &:({\color{Teal}-3}, {\color{DarkOrange} 3}) \rightarrow ({\color{DarkOrange}3}, {\color{Teal} -3})\phantom{x}\\B \rightarrow B^{\prime} &:({\color{Teal}-3}, {\color{DarkOrange} 1}) \rightarrow ({\color{DarkOrange}1}, {\color{Teal} -3})\\C \rightarrow C^{\prime} &: ({\color{Teal}-1}, {\color{DarkOrange} 1}) \rightarrow ({\color{DarkOrange} 1}, {\color{Teal} -1})\\D \rightarrow D^{\prime} &: ({\color{Teal}-1},{\color{DarkOrange} 3}) \rightarrow ({\color{DarkOrange}3}, {\color{Teal} -1})\end{aligned}

This means that the image of the square has the following vertices: $A=(3, -3)$, $B=(1, -3)$, $C=(1, -1)$, and $D=(3, -1)$.

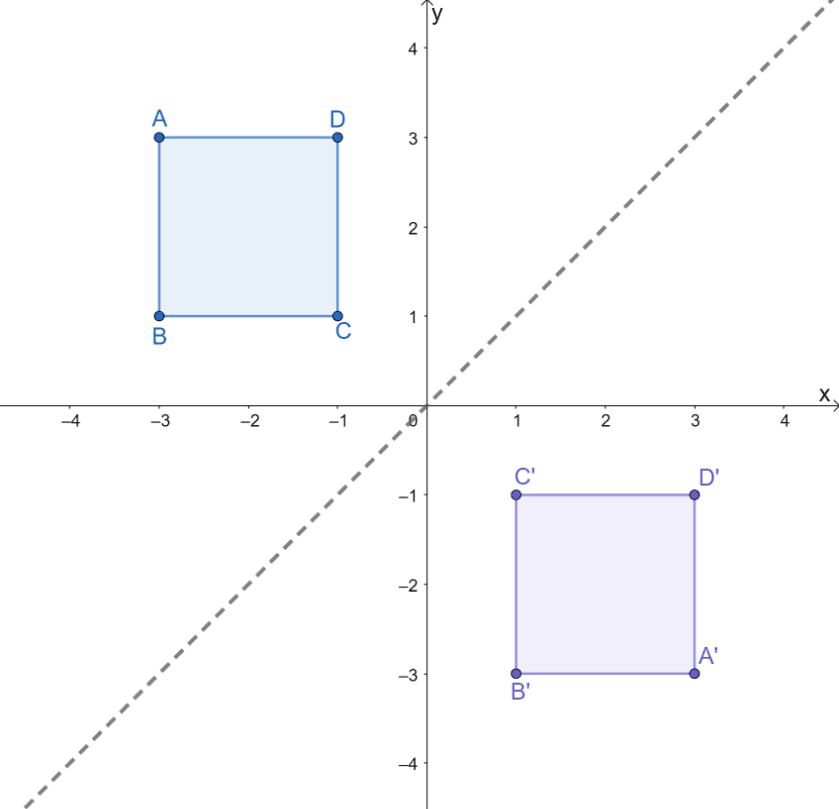
reflecting the square over the line of reflection y

Use the coordinates to graph each square — the image is going to look like the pre-image but flipped over the diagonal (or $y = x$).

Practice Questions

1. Suppose that the point $(-4, -5)$ is reflected over the line of reflection $y =x$, what is the resulting image’s new coordinate?

A. $(4,5)$
B. $(-4,-5)$
C. $(5,4)$
D. $(-5,-4)$

2.The square $ABCD$ has the following vertices: $A=(2, 0)$, $B=(2,-2)$, $C=(4, -2)$, and $D=(4, 0)$. When the square is reflected over the line of reflection $y =x$, what are the vertices of the new square? 

A. $A=(0, -2)$, $B=(-2,-2)$, $C=(-2,-4)$, and $D=(0,-4)$
B. $A=(0, 2)$, $B=(-2, 2)$, $C=(-2, 4)$, and $D=(0, 4)$
C. $A=(0,-2)$, $B=(2,-2)$, $C=(2,-4)$, and $D=(0,-4)$
D. $A=(0,2)$, $B=(-2,2)$, $C=(-2, 4)$, and $D=(0,4)$

Answer Key

1. D
2. B

Images/mathematical drawings are created with GeoGebra.