- Home
- >
- 10 times table – Explanation & Examples
JUMP TO TOPIC
10 Times Table – Explanation & Examples
 The 10 times table is one of the most commonly used tables for solving mathematical problems related to fractions, division, L.C.M, H.C.F, and multiplication. It is also one of the easiest tables to learn and memorize.
The 10 times table is one of the most commonly used tables for solving mathematical problems related to fractions, division, L.C.M, H.C.F, and multiplication. It is also one of the easiest tables to learn and memorize.
The 10 times table is a table that contains multiples of the number 10.
Learning and understanding the 10 times table is quite easy. This topic will provide interesting tips and techniques to learn and understand the 10 times table quickly and easily.
You should refresh the following concepts to understand this topic easily.
- Basics of addition and multiplication
- 5 times table
10 Multiplication Table
We can write the table of 10 as:
- $10\times1 = 10$
- $10 \times 2 = 20$
- $10 \times 3 = 30$
- $10 \times 4 =40$
- $10 \times 5 =50$
- $10\times 6 =60$
- $10\times 7 = 70$
- $10\times 8 = 80$
- $10\times 9 = 90$
- $10\times 10 = 100$
Tips To Quickly Learn the 10 Times Table
Let us look at some simple tips which can help you memorize the 10 times table easily.
Adding zero at the end: This is the golden method to help students memorize the 10 times table. All you have to do is add a zero at the end of every number multiplied by 10. For example, suppose 10 is multiplied by 4. If we add a zero at the end of 4, we get 40, which is the same as $10 \times 4 = 40$. The table below shows that by adding a zero to the digit multiplied by 10, we get the 10 times table.
| 10 Times Table | Adding Zero at the end (Outcome of 10 Times Table) |
10 x 1 | 10 |
10 x 2 | 20 |
10 x 3 | 30 |
10 x 4 | 40 |
10 x 5 | 50 |
10 x 6 | 60 |
10 x 7 | 70 |
10 x 8 | 80 |
10 x 9 | 90 |
10 x 10 | 100 |
Using the 5 times table: The above method is sufficient for students to understand the 10 times table, but if students want to learn the 10 times table while also revising the 5 times table, this method is perfect. In this method, the outcomes of the 5 times table are doubled, which gives us the multiples of 10. For example, $5 \times 3 =15$; if we double it, we get 30 which is the 3rd multiple of 10.
5 Times Table | Double Value |
5 x 1 = 5 | 5+5 or 5 x 2 = 10 |
5 x 2 = 10 | 10+10 or 10 x 2 = 10 |
5 x 3 = 15 | 15+15 or 15 x 2 = 10 |
5 x 4 = 20 | 20+20 or 20 x 2 = 10 |
5 x 5 = 25 | 25+25 or 25 x 2 = 10 |
5 x 6 = 30 | 30+30 or 30 x 2 = 10 |
5 x 7 = 35 | 35+35 or 35 x 2 = 10 |
5 x 8 = 40 | 40+40 or 40 x 2 = 10 |
5 x 9 = 45 | 45+45 or 45 x 2 = 10 |
5 x 10 = 50 | 50+50 or 50 x 2 = 10 |
Addition: This is an easy method to learn any table, and it also helps students develop good addition skills. As the name suggests, it involves simple addition. For example, we start with the digit 0. If we add 10 to it, we get the first multiple of 10. We can work out the next multiple of 10 by adding 10 to the current answer and so on, as shown in the picture below.
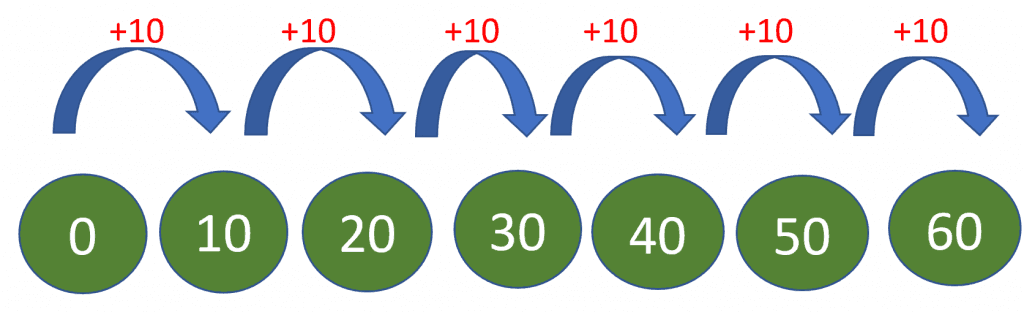
Table of 10 From 1 to 20:
We can write a complete table of 10 from 1 to 20 as:
| Numerical Representation | Descriptive Representation | Product (Outcome) |
| $10 \times 1$ | Ten times one | $10$ |
| $10 \times 2$ | Ten times two | $20$ |
| $10 \times 3$ | Ten times three | $30$ |
| $10 \times 4$ | Ten times four | $40$ |
| $10\times 5$ | Ten times five | $50$ |
| $10 \times 6$ | Ten times six | $60$ |
| $10 \times 7$ | Ten times seven | $70$ |
| $10 \times 8$ | Ten times eight | $80$ |
| $10 \times 9$ | Ten times nine | $90$ |
| $10 \times 10$ | Ten times ten | $100$ |
| $10 \times 11$ | Ten times eleven | $110$ |
| $10 \times 12$ | Ten times twelve | $120$ |
| $10 \times 13$ | Ten times thirteen | $130$ |
| $10 \times 14$ | Ten times fourteen | $140$ |
| $10 \times 15$ | Ten times fifteen | $150$ |
| $10 \times 16$ | Ten times sixteen | $160$ |
| $10 \times 17$ | Ten times seventeen | $170$ |
| $10 \times 18$ | Ten times eighteen | $180$ |
| $10 \times 19$ | Ten times nineteen | $190$ |
| $10 \times 20$ | Ten times twenty | $200$ |
Example 1: Mason gets 10 dollars of pocket money daily. Calculate the total amount of pocket money received by Mason, If:
- The year is a leap year
- The year is normal (not a leap year)
Solution:
- Leap year has 366 days. So the total amount of pocket money received by Mason in a leap year would be $366 \times 10 = 3660$ dollars. As discussed earlier, we add a zero at the end of 366 to get the answer.
- Normal Year has 365 days. So the total amount of pocket money received by Mason in a normal year would be $365 \times 10 = 3650$ dollars.
Example 2: Calculate 10 times 5 times 10.
Solution:
10 times 5 times 10 can be written as:
$ 10\times 5 \times 10$
$ = 50\times 10$
$ = 500$
Example 3: Calculate 8 times 10 plus 7 minus 2 times 10.
Solution:
8 times 10 plus 7 minus 2 times 10 can be written as:
$(8\times 10) +7 -2\times 10$
$ = (8\times 10) +7+ (-2\times 10)$
$ = 80 + 7 – 20$
$ = 87- 20$
$ = 67$
Example 4: Sarah received a bag full of candies on her birthday. The bag contained a total of 100 candies. Sarah got super excited and started to think about how many candies she should eat daily. Using the 10 times table, help Sarah calculate how many days the candies would last if:
- She eats 5 candies daily
2. She eats 10 candies daily
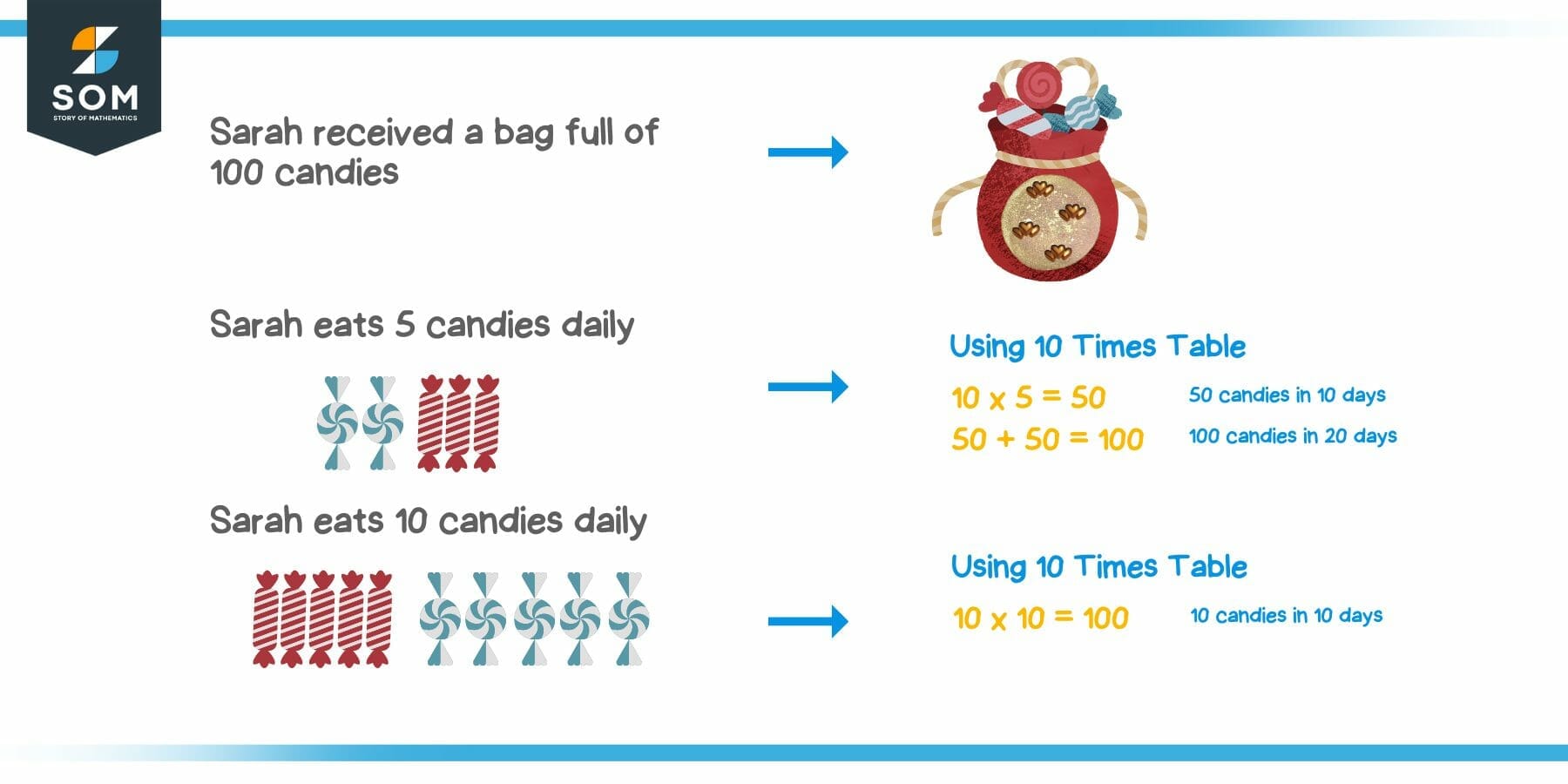
Solution:
- Suppose Sarah eats 5 candies a day, then using the 10 times table, $10\times 5 = 50$ candies. So Sarah will eat 50 candies in 10 days and 50 candies in the next 10 days. Sarah will finish 100 candies in 20 days.
Alternatively, this can also be solved using the 5 times table.
We know that $5 \times 20 = 100$ candies. So Sarah finishes all the candies in 20 days.
2. If Sarah eats 10 candies a day, then using the 10 times table, $10\times 10 = 100$ candies. So if Sarah eats 10 candies daily, she will finish all the candies in 10 days.
Practice Questions:
- Steve and Chris are playing tag, and one tag is equal to 10 points. The person who scores 150 points first will win the game. Using 10 times table calculate the total number of tags needed to win the game.
- Calculate 10 times 2 times 10.
- What is the 9th multiple of 10?
- Calculate 5 times 10 times 2 minus 100.
- Calculate 5 times 7 using the 10 times table.
- From the given table, select the numbers which are multiples of 10.
| 18 | 37 | 16 | 160 | 50 | 51 | 61 | 880 |
| 25 | 19 | 20 | 18 | 10 | 300 | 67 | 654 |
| 90 | 11 | 13 | 17 | 400 | 403 | 99 | 321 |
| 15 | 230 | 14 | 16 | 30 | 504 | 33 | 129 |
| 310 | 295 | 200 | 25 | 21 | 87 | 41 | 410 |
| 32 | 14 | 55 | 29 | 130 | 88 | 29 | 220 |
| 41 | 32 | 39 | 34 | 35 | 1000 | 110 | 219 |
| 37 | 100 | 260 | 39 | 80 | 600 | 150 | 231 |
| 41 | 65 | 43 | 51 | 45 | 122 | 114 | 257 |
| 44 | 43 | 590 | 49 | 60 | 132 | 215 | 309 |
Answer Key
1. Using the 10 times table, $10 \times 15 = 150$. So 15 tags are needed to win the game.
2. 10 times 2 times 10 can be written as:
$ 10\times 2 \times 10$
$ = 20 \times 10 = 200$
3. Multiples of 10 can be written as: 10, 20, 30, 40, 50, 60, 70, 80, 90, and 100
So the 9th multiple is 90.
4. 5 times 10 times 2 minus 100 can be written as:
$ = (5\times 10 \times 2) -100$
$ = (50 \times 2) -100$
$ = 100 – 100$
$ = 0$
5. We know that if we double the values of the 5 times table, we get the 10 times table. This also means that if we half the values of the 10 times table, we should get the 5 times table. Using the 10 times table, we know that $10 \times 7 = 70$. If we find the half value of $70$, we get $35$. Hence, $5 \times 7 = 35$.
6.
| 18 | 37 | 16 | 160 | 50 | 51 | 61 | 880 |
| 25 | 19 | 20 | 18 | 10 | 300 | 67 | 654 |
| 90 | 11 | 13 | 17 | 400 | 403 | 99 | 321 |
| 15 | 230 | 14 | 16 | 30 | 504 | 33 | 129 |
| 310 | 295 | 200 | 25 | 21 | 87 | 41 | 410 |
| 32 | 14 | 55 | 29 | 130 | 88 | 29 | 220 |
| 41 | 32 | 39 | 34 | 35 | 1000 | 110 | 219 |
| 37 | 100 | 260 | 39 | 80 | 600 | 150 | 231 |
| 41 | 65 | 43 | 51 | 45 | 122 | 114 | 257 |
| 44 | 43 | 590 | 49 | 60 | 132 | 215 | 309 |
