- Home
- >
- 11 times table – Explanation & Examples
JUMP TO TOPIC
11 Times Table – Explanation & Examples
 The 11 times table is the multiplication table for the number 11. Eleven is a prime number, but unlike the prime number 7, the table of 11 is quite easy to familiarize with.
The 11 times table is the multiplication table for the number 11. Eleven is a prime number, but unlike the prime number 7, the table of 11 is quite easy to familiarize with.
The 11 times table is a table that contains multiples of the number 11.
Learning and understanding the 11 times table is essential for solving multiplication, division, and factorization problems. This topic will present some tips that will help students memorize the 11 times table.
To understand this topic easily, please review the following concepts:
- Basics of addition and multiplication
- 10 times table
11 Multiplication Table
We can write the table of 11 as:
- $11\times 1 = 11$
- $11\times 2 = 22$
- $11\times 3 = 33$
- $11\times 4 =44$
- $11 \times 5 =55$
- $11 \times 6 =66$
- $11 \times 7 = 77$
- $11 \times 8 = 88$
- $11 \times 9 = 99$
- $11 \times 10 = 110$
Tips on Learning the 11 Times Table
Let us look at some simple tips which can help you memorize the 11 times table.
Digits pattern for the first 9 multiples: The first nine multiples follow a simple pattern. The number which is multiplied by 11 is repeated twice in the product. For example, $11\times 1 = 11$, as 11 is multiplied by the number 1, 1 is repeated in the answer which is 11. Similarly, $11\times 6 =66$, here 6 is repeated. The whole pattern is presented below, and the repeated digits are shown in green color.
11 Times Table | Table Outcome |
11 x 1 | 11 |
11 x 2 | 22 |
11 x 3 | 33 |
11 x 4 | 44 |
11 x 5 | 55 |
11 x 6 | 66 |
11 x 7 | 77 |
11 x 8 | 88 |
11 x 9 | 99 |
Pattern for the 10th and higher multiples of 11: This method presents the pattern followed by the 10th and the higher multiples of the number 11. Suppose 11 is multiplied by 10 (note that the unit digit of 10 is 0 and the tens digit is 1); the product of $11 \times 10$ is equal to 110 (unit digit 0, tens digit 1, and hundreds digit 1). The unit digit of the product is the same as the unit digit of the number multiplied by 11.
The tens digit of the product is the summation of the unit and the tens digit. In our example, 10 is being multiplied by 11, so the tens digit of the product is $0+1 = 1$. Lastly, the hundreds digit of the product is the same as the tens digit of the number multiplied by 11. In short, the unit and hundreds digit of the number 10 are equal to the unit and tens digit of the product, i.e., 110. Meanwhile the ten’s digit of the product is the summation of the unit and tens digit of 10, i.e., $1+0 =1$.
This pattern is presented in the table below. Note that the only exception is the 19th multiple of 11. The summation of the unit and ten’s digit of 19 leads to $1+9 =10$. So 0 will be the ten’s digit of the product while 1 will be added in the hundred’s digit of the product, and it will become $1+1 =2$, as shown in the table below.
11 Times Table | Outcome | Unit Digit of Product | Ten’s Digit of Product | Hundred’s Digit of Product |
11 x 10 | 110 | 0 | 1 + 0 = 1 | 1 |
11 x 11 | 121 | 1 | 1 + 1 = 2 | 1 |
11 x 12 | 132 | 2 | 1 + 2 = 3 | 1 |
11 x 13 | 143 | 3 | 1 + 3 = 4 | 1 |
11 x 14 | 154 | 4 | 1 + 4 = 5 | 1 |
11 x 15 | 165 | 5 | 1 + 5 = 6 | 1 |
11 x 16 | 176 | 6 | 1 + 6 = 7 | 1 |
11 x 17 | 187 | 7 | 1 + 7 = 8 | 1 |
11 x 18 | 198 | 8 | 1 + 8 = 9 | 1 |
11 x 19 | 209 | 9 | 1 + 9 = 10 | 2 |
11 x 20 | 220 | 0 | 2 + 0 = 2 | 2 |
Using the 10 times table: This is one of the easiest methods to learn the 11 times table, if you have already memorized the 10 times table. If we add natural numbers to multiples of the number 10, we get the 11 times table.
The first multiple of 10 is added with the first natural number which is 1. Similarly, the second multiple of 10 is added with the second natural number 2. This method is presented in the table below.
10 Times Table | Addition | (Addition outcome) | 11 Times Table |
10 x 1 = 10 | 10 + 1 | 11 | 11 x 1 = 11 |
10 x 2 = 20 | 20 + 2 | 22 | 11 x 2 = 22 |
10 x 3 = 30 | 30 + 3 | 33 | 11 x 3 = 33 |
10 x 4 = 40 | 40 + 4 | 44 | 11 x 4 =44 |
10 x 5 = 50 | 50 + 5 | 55 | 11 x 5 =55 |
10 x 6 = 60 | 60 + 6 | 66 | 11 x 6 =66 |
10 x 7 = 70 | 70 + 7 | 77 | 11 x 7 = 77 |
10 x 8 = 80 | 80 + 8 | 88 | 11 x 8 = 88 |
10 x 9 = 90 | 90 + 9 | 99 | 11 x 9 = 99 |
10 x 10 = 100 | 100 + 10 | 110 | 11 x 10 = 110 |
Table of 11 From 1 to 20
We can write a complete table of 11 from 1 to 20 as:
Numerical Representation | Descriptive Representation | Product (Table Outcome) |
$11 \times 1$ | Eleven times one | $11$ |
$11 \times 2$ | Eleven times two | $22$ |
$11 \times 3$ | Eleven times three | $33$ |
$11 \times 4$ | Eleven times four | $44$ |
$11 \times 5$ | Eleven times five | $55$ |
$11 \times 6$ | Eleven times six | $66$ |
$11 \times 7$ | Eleven times seven | $77$ |
$11 \times 8$ | Eleven times eight | $88$ |
$11\times 9$ | Eleven times nine | $99$ |
$11\times 10$ | Eleven times ten | $110$ |
$11\times 11$ | Eleven times eleven | $121$ |
$11\times 12$ | Eleven times twelve | $132$ |
$11\times 13$ | Eleven times thirteen | $143$ |
$11\times 14$ | Eleven times fourteen | $154$ |
$11\times 15$ | Eleven times fifteen | $165$ |
$11 \times 16$ | Eleven times sixteen | $176$ |
$11 \times 17$ | Eleven times seventeen | $187$ |
$11\times 18$ | Eleven times eighteen | $198$ |
$11 \times 19$ | Eleven times nineteen | $209$ |
| $11 \times 20$ | Eleven times twenty | $220$ |
Example 1: Calculate 11 times 4 times 2 minus 40.
Solution:
11 times 4 times 2 minus 40 can be written as:
$ 11\times4 \times 2 – 40$
$ =44\times 2 – 40$
$ = 88 – 40$
$ = 48$
Example 2: Verify whether the 7th multiple of 11 is 77 or not.
Solution:
We know the first 7 multiples of 11 are 11, 22, 33, 44, 55, 66, and 77.
We can also verify it through the addition method.
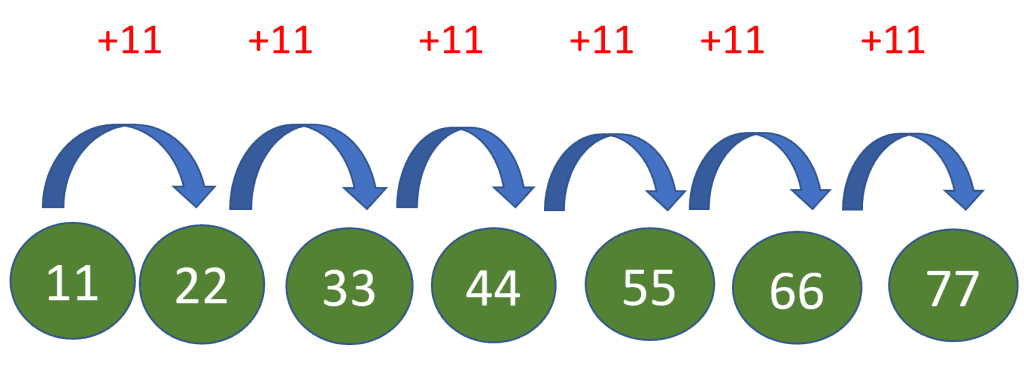
Hence, we can confirm that the 7th multiple of 11 is 77.
Example 3: May has enough chocolates to give her 3 friends 11 chocolates each. Calculate the total number of chocolates she has.
Solution:
May distributes 11 chocolates each to 3 friends.
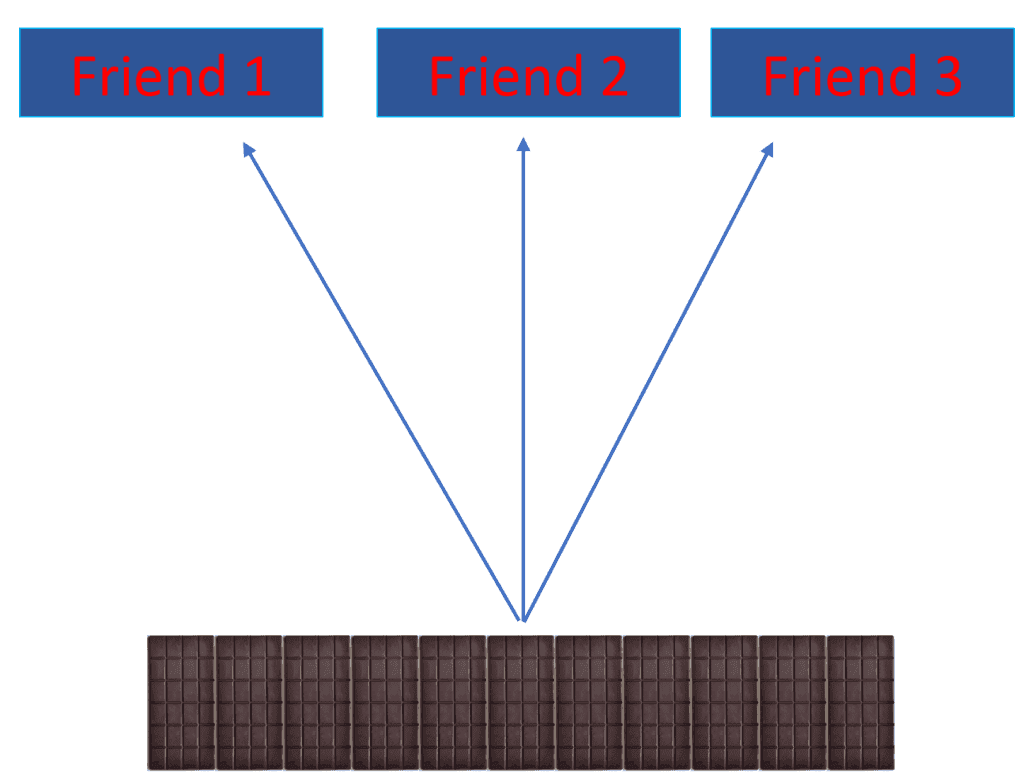
By using the 11 times table, we can calculate the total number of chocolates.
$11\times 3 = 33$ chocolates
Example 4: Using the digit pattern method, find the values of
- 11 times 43
- 11 times 52
Solution:
To find $11 \times 43$, we note that the unit digit of the product would be the same as the unit digit of $43$, i.e., 3. The hundredth digit of the product would the same as the tens digit of $43$, i.e., 4, and the tens digit of the product would be the sum of $4$ and $3$, i.e., 7. Hence, the product is 473.
To find $11 \times 52$, we note that the unit digit of the product would be the same as the unit digit of $52$, i.e., 2. The hundredth digit of the product would the same as the tens digit of $52$, i.e., 5, and the tens digit of the product would be the sum of 5 and 2, i.e., 7. Hence, the product is 572.
Practice Questions:
- Suppose one bag can contain four balls. Calculate the total number of balls if you have 11 bags.
- Calculate 11 times 2 times 2.
- Find the value of “Y”, if $Y \times 11 = 11\times 4 – 11$.
- From the given table, select the numbers which are multiples of 11.
37 21 22 35 55 61 15 19 14 72 10 53 16 66 28 17 15 11 30 47 09 16 29 99 51 63 77 15 84 94 121 44 42 49 88 110 93 73 71 74 65 115 99 57 54 99 51 132 221 82 72 51 65 199 44 48 56 89 60 220
Answer Key
1) We know that one bag contains 4 balls.

So 11 bags will have $11\times 4 = 44$ balls.
2) We can write 11 times 2 times 2 as:
$ 11\times 2 \times 2$
$ = 22 \times 2$
$ = 44$
3) $ Y \times 11 = 11\times 4 – 11$
$ Y \times 11 = 44 – 11 $
$ Y \times 11 = 33 $
We know $11\times 3 =33$, so $ Y = 3 $.
4)
| 37 | 21 | 22 | 35 | 55 | 61 |
| 15 | 19 | 14 | 72 | 10 | 53 |
| 16 | 66 | 28 | 17 | 15 | 11 |
| 30 | 47 | 09 | 16 | 29 | 99 |
| 51 | 63 | 77 | 15 | 84 | 94 |
| 121 | 44 | 42 | 49 | 88 | 110 |
| 93 | 73 | 71 | 74 | 65 | 115 |
| 99 | 57 | 54 | 99 | 51 | 132 |
| 221 | 82 | 72 | 51 | 65 | 199 |
| 44 | 48 | 56 | 89 | 60 | 220 |
