JUMP TO TOPIC
12 Times Table – Explanation & Examples
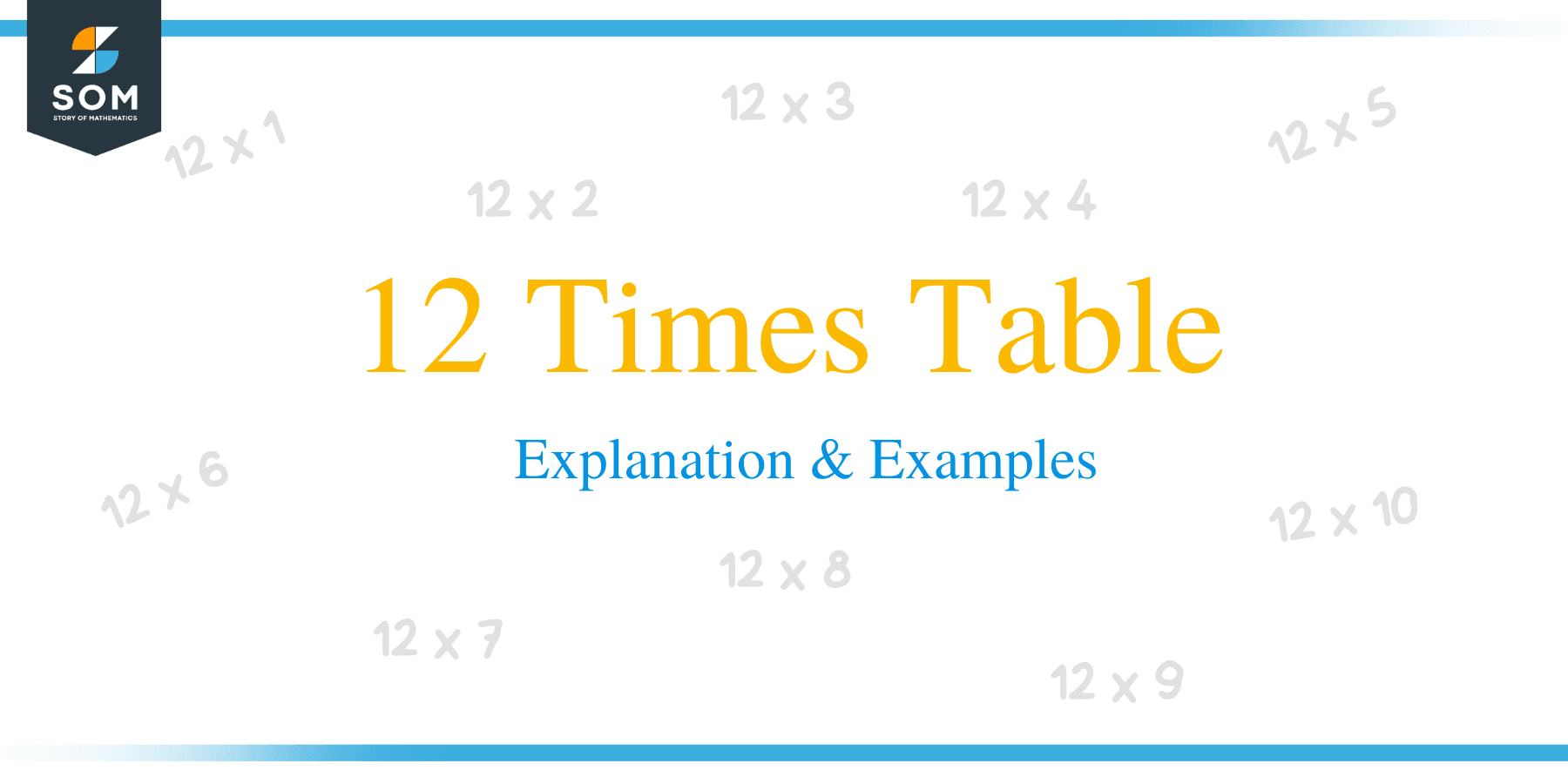The 12 times table is the multiplication table of the number 12. We encounter the number 12 and its multiples quite often in our daily life. For example, we divide our day and nights into 12 equal hours and divide a year into 12 months. Many grocery items such as eggs also come in packs of 12 (i.e., a dozen). So, learning the 12 times table will come in handy in solving many problems related to the multiples of 12 that we encounter every day.
The 12 times table is a table that contains the multiples of the number 12.
The 12 times table does not follow any simple pattern or rules; still, we will present some tips and patterns that will help you learn and memorize the 12 times table.
You should refresh the following concepts to understand the material discussed here.
- Basics of addition and multiplication
- 2 times table
- 6 times table
- 10 times table
12 Multiplication Table
The table of 12 can be written as:
- $12\times 1 = 12$
- $12\times 2 = 24$
- $12\times 3 = 36$
- $12\times 4 =48$
- $12 \times 5 =60$
- $12 \times 6 =72$
- $12 \times 7 = 84$
- $12 \times 8 = 96$
- $12 \times 9 = 108$
- $12 \times 10 = 120$
Different Tips for the 12 Times Table:
Let us look at some simple tips which can help you memorize the 12 times table.
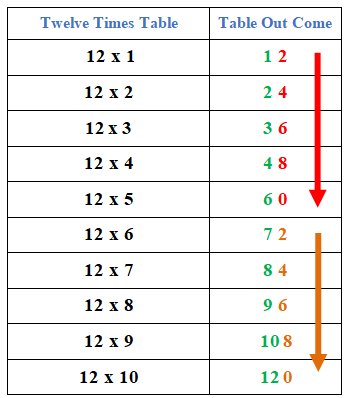
Digits Pattern: Just like the 4 and 8 times table, the 12 times table follows a digit pattern of five multiples. This digit pattern repeats itself after every five multiples. In this pattern, the ten’s digits of the first five multiples are 2, 4, 6, 8 and 0. The same sequence is repeated for the next five multiples and so on. The said pattern is shown in the table below.
Using the 10 and the 2 Times Tables: This is one of the easiest methods to learn the 12 times tables as it requires the usage of the10 and the 2 times tables, which are the easiest tables to remember. If we add each outcome of the 10 times table to the 2 times table, the outcome will be the 12 times table. For example, the third multiple of 10 is 30, and the third multiple of 2 is 6, and if we add 30 and 6, we get 36 that is the third multiple of 12. The detailed method is presented in the table below.
10 Times Table | 2 Times Table | Addition | Outcome |
| $10\times 1 = {\color{green}10}$ | $ 2 \times 1 = 2$ | ${\color{green}10} + {\color{red}2}$ | $12$ |
| $10\times 2 = {\color{green}20}$ | $2 \times 2 = 4$ | ${\color{green}20} + {\color{red}4}$ | $ 24 $ |
| $10\times 3 = {\color{green}30}$ | $2 \times 3 = 6$ | ${\color{green}30} + {\color{red}6}$ | $36$ |
| $10\times 4 = {\color{green}40}$ | $2 \times 4 = 8$ | ${\color{green}40} + {\color{red}8}$ | $48$ |
| $10\times 5 = {\color{green}50}$ | $2 \times 5 = 10$ | ${\color{green}50} +{\color{red}10}$ | $60$ |
| $10\times 6 = {\color{green}60}$ | $2 \times 6 = 12$ | ${\color{green}60} +{\color{red}12}$ | $72$ |
| $10\times 7 = {\color{green}70}$ | $2 \times 7 = 14$ | ${\color{green}70} +{\color{red}14}$ | $84$ |
| $10\times 8 = {\color{green}80}$ | $2 \times 8 = 16$ | ${\color{green}80} + {\color{red}16}$ | $96$ |
| $10\times 9 = {\color{green}90}$ | $2 \times 9 = 18$ | ${\color{green}90} + {\color{red}18}$ | $108$ |
| $10\times 10 = {\color{green}100}$ | $2 \times 10 = 20$ | ${\color{green}100} + {\color{red}20}$ | $120$ |
Using the 6 Times Table: This method is quite simple, and it will help you in the revision of the 6 times table. If we double the answers/ multiples of the 6 times table, then the resulting multiples/ outcomes will form the 12 times table. For example, $6\times 6 = 36$, if we double the answer, i.e., $36 + 36 = 72$, then it is the same as $12\times 6 = 72$. This method is presented in the table below.
| 6 Times Table | Double the Answer | Multiples of 12 |
| $6\times 1 = {\color{green}6}$ | ${\color{green}6} + {\color{green}6} = {\color{red}12}$ | ${\color{red}12}$ |
| $6\times 2 = {\color{green}12}$ | ${\color{green}12} + {\color{green}12} = {\color{red}24}$ | ${\color{red}24}$ |
| $6\times 3 = {\color{green}18}$ | ${\color{green}18} + {\color{green}18} = {\color{red}36}$ | ${\color{red}36}$ |
| $6\times 4 = {\color{green}24}$ | ${\color{green}24} + {\color{green}24} = {\color{red}48}$ | ${\color{red}48}$ |
| $6\times 5 = {\color{green}30}$ | ${\color{green}30} + {\color{green}30} = {\color{red}60}$ | ${\color{red}60}$ |
| $6\times 6 = {\color{green}36}$ | ${\color{green}36} + {\color{green}36} = {\color{red}72}$ | ${\color{red}72}$ |
| $6\times 7 = {\color{green}42}$ | ${\color{green}42} + {\color{green}42} = {\color{red}84}$ | ${\color{red}84}$ |
| $6\times 8 = {\color{green}48}$ | ${\color{green}48} + {\color{green}48} = {\color{red}96}$ | ${\color{red}96}$ |
| $6\times 9 = {\color{green}54}$ | ${\color{green}54} + {\color{green}54} = {\color{red}108}$ | ${\color{red}108}$ |
| $6\times 10 = {\color{green}60}$ | ${\color{green}60} + {\color{green}60} = {\color{red}120}$ | ${\color{red}120}$ |
Table of 12 From 1 to 20:
A complete table of 12 from 1 to 20 can be written as:
Numerical Representation | Descriptive Representation | Product (Answer) |
| $12 \times 1$ | Twelve times one | $12$ |
| $12 \times 2$ | Twelve times two | $24$ |
| $12 \times 3$ | Twelve times three | $36$ |
| $12 \times 4$ | Twelve times four | $48$ |
| $12 \times 5$ | Twelve times five | $60$ |
| $12 \times 6$ | Twelve times six | $72$ |
| $12 \times 7$ | Twelve times seven | $84$ |
| $12 \times 8$ | Twelve times eight | $96$ |
| $12 \times 9$ | Twelve times nine | $108$ |
| $12 \times 10$ | Twelve times ten | $120$ |
| $12 \times 11$ | Twelve times eleven | $132$ |
| $12 \times 12$ | Twelve times twelve | $144$ |
| $12 \times 13$ | Twelve times thirteen | $156$ |
| $12 \times 14$ | Twelve times fourteen | $168$ |
| $12 \times 15$ | Twelve times fifteen | $180$ |
| $12 \times 16$ | Twelve times sixteen | $192$ |
| $12 \times 17$ | Twelve times seventeen | $204$ |
| $12 \times 18$ | Twelve times eighteen | $216$ |
| $12 \times 19$ | Twelve times nineteen | $228$ |
| $12 \times 20$ | Twelve times twenty | $240$ |
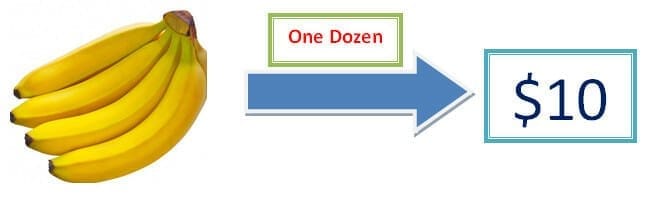
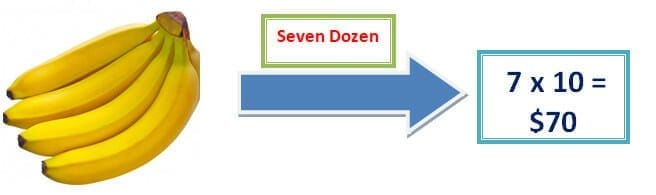
Example 1: Suppose a dozen bananas cost you 10 dollars. Calculate the amount needed to purchase 84 bananas.
Solution:
We know that one dozen = 12. So, 12 bananas can be purchased for 10 dollars.
By using 12 times table we know, $12 \times 7 = 84 $. So, 84 bananas = 7 dozen bananas. If one dozen cost us 10 dollars. Then, seven dozen will cost us $7 \times 10 = 70$ dollars.
Example 2: Calculate 12 times 10 time 2 minus 100.
Solution:
12 times 10 times 2 minus 100 can be written as:
$ = 12\times10 \times 2 – 100$
$ = 12\times 20 – 100$
$ = 240 – 100$
$ = 140$
Example 3: What is the 9th multiple of 12?
Solution:
We know the first 10 multiples of 12 are 12, 24, 36, 48, 60, 72, 84, 96, 108, and 120.
So, the 9th multiple is 108.
Example 4: A car covers 12 KM in an hour. Calculate the distance covered by the car in 13 hours.
Solution:
We know that the car covers 12KM in one hour. So, by using the 12 times table, we can calculate the distance covered by the car in 13 hours.
$12 \times 13 = 156$ KM.
Practice Questions:
1) Calculate the total amount of eggs eaten by Patrick in a week. If
- Patrick eats a dozen eggs daily.
- Patrick eats half a dozen eggs daily.
2) A Sportscar driver completes 4 laps in 12 minutes. How many laps will it complete?
- In 24 minutes
- In 48 minutes
- In 1 hour
3) Find the value of $Y$ if “$ Y \times 12 = 6 \times 2 + 12 \times 6$.’’
4) From the given table, select the numbers which are multiples of 12.
| 39 | 38 | 18 | 24 | 58 | 61 |
| 41 | 42 | 14 | 78 | 19 | 56 |
| 108 | 96 | 72 | 74 | 66 | 68 |
| 120 | 41 | 49 | 12 | 18 | 33 |
| 59 | 240 | 216 | 11 | 114 | 112 |
| 121 | 44 | 42 | 49 | 36 | 110 |
| 93 | 73 | 71 | 179 | 65 | 115 |
| 99 | 157 | 154 | 99 | 151 | 132 |
| 221 | 84 | 77 | 51 | 65 | 96 |
| 44 | 48 | 56 | 89 | 60 | 220 |
Answer Key:
1) We have to calculate the total amount of eggs eaten by Patrick in seven days.
- If Patrick eats a dozen eggs daily
Then, the total amount of eggs eaten in a week can be calculated by using 12 times table
$12\times 7 = 84$ eggs.
- If Patrick eats half a dozen eggs daily
We know 1 dozen = 12 So, half dozen = 6
$6\times 7 = 42$ eggs.
2) Sportscar completes 4 laps in 12 minutes
- By using 12 times table, we know $12\times 2 = 24$. So, if we multiply 4 by 2 we get the total amount of laps completed by sportscar in 24 minutes, i.e., $4\times 2 = 8$ laps in 24 minutes.
- $12\times 4 = 48$. So, multiplying 4 by 4, i.e., $4\times 4 =16$ laps in 48 minutes
- $12\times 5 = 60$ mins or 1 hour. So, multiplying 4 by 5 we get, $4\times 5 = 20$ laps in an hour.
3) $ Y \times 12 = 6 \times 2 + 12 \times 6$
$ Y \times 12 = 12 + 72 $.
$ Y \times 12 = 84 $.
We know $7\times 12 =84$
$ Y = 7 $.
4)
| 39 | 38 | 18 | 24 | 58 | 61 |
| 41 | 42 | 14 | 78 | 19 | 56 |
| 108 | 111 | 72 | 74 | 66 | 68 |
| 120 | 41 | 49 | 12 | 18 | 33 |
| 59 | 240 | 216 | 11 | 114 | 112 |
| 121 | 44 | 42 | 49 | 36 | 110 |
| 93 | 73 | 71 | 179 | 65 | 115 |
| 99 | 157 | 154 | 99 | 151 | 132 |
| 221 | 84 | 77 | 51 | 65 | 96 |
| 44 | 48 | 56 | 89 | 60 | 220 |