- Home
- >
- 13 Times Table – Explanation & Examples
JUMP TO TOPIC
13 Times Table – Explanation & Examples
 The 13 times table is the multiplication table of the number 13. The number 13 is considered a lucky number in some cultures and unlucky in others. We do not know whether 13 is lucky or unlucky, but we do know that it is a prime number that makes the 13 times table difficult to learn and memorize. Yet, it is worthwhile to learn the 13 times table as it will help you solve complex multiplication and division-related problems.
The 13 times table is the multiplication table of the number 13. The number 13 is considered a lucky number in some cultures and unlucky in others. We do not know whether 13 is lucky or unlucky, but we do know that it is a prime number that makes the 13 times table difficult to learn and memorize. Yet, it is worthwhile to learn the 13 times table as it will help you solve complex multiplication and division-related problems.
The 13 times table is a table that contains the multiples of the number 13.
Learning and understanding the 13 times table is essential for solving multiplication, division, H.C.F, L.C.M, and factorization-related mathematical problems. In this topic, we will present some tips and patterns that will help you learn and memorize the 13 times table.
You should refresh the following concepts to understand the material discussed here.
- Basics of addition and multiplication
- 3 Times Table
- 4 Times Table
- 10 Times Table
13 Multiplication Table
We can write the table of 13 as:
- $13 \times 1 = 13$
- $13 \times 2 = 26$
- $13 \times 3 = 39$
- $13 \times 4 =52$
- $13 \times 5 =65$
- $13 \times 6 =78$
- $13 \times 7 = 91$
- $13 \times 8 = 104$
- $13 \times 9 = 117$
- $13 \times 10 = 130$
Different Tips for the 13 Times Table:
Let us look at some simple tips which can help you memorize the 13 times table.
Digits Pattern of the 3 Times Table: As the name suggests, you have to follow the digits pattern of the 3 times table to help you memorize the 13 times table. The last digits of the first 10 multiples of the 3 times table are also the last digits of the first 10 multiples of the 13 times table. The pattern is illustrated in the table below.
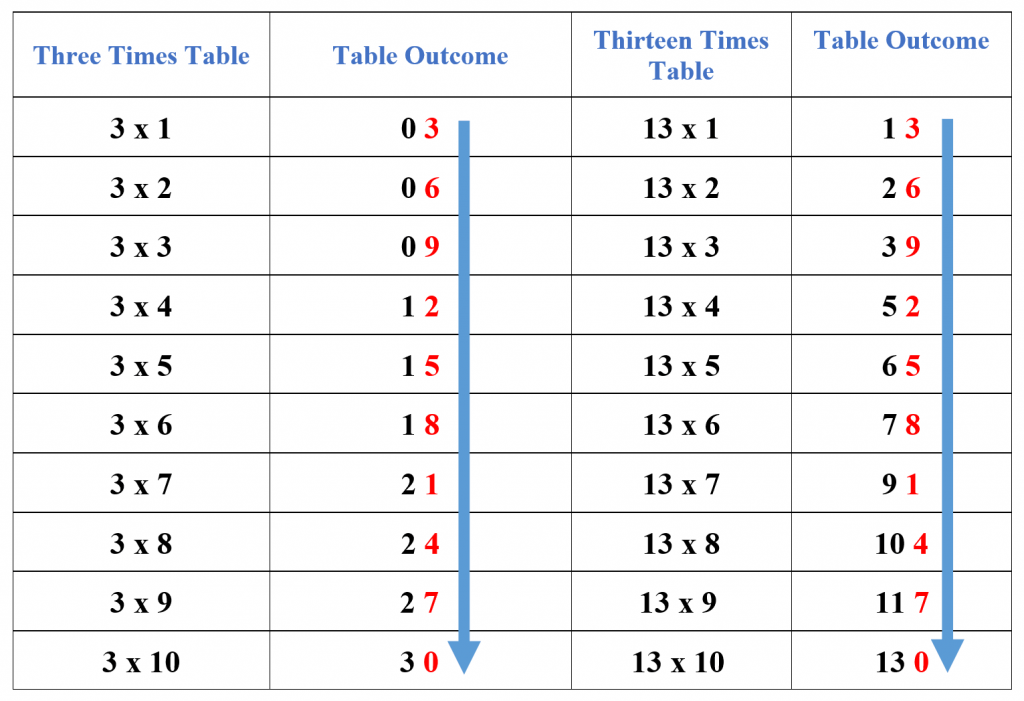
Using the 10 and the 3 Times Tables: This is one of the easiest methods to learn the 13 times tables as it requires the usage of the 10 and the 3 times tables which are quite easy to remember. If we add each multiple of the 10 times table to the same multiple of the 3 times table, the result will be a multiple of the 13 times table. For example, the fifth multiple of 10 is 50, and the fifth multiple of 3 is 15, and if we add 50 and 15, we get 65 that is the fifth multiple of 13. The detailed method is presented in the table below.
10 Times Table | 3 Times Table | Addition | Outcome |
$10\times 1 = {\color{green}10}$ | $ 3 \times 1 = {\color{red}3}$ | ${\color{green}10}+ {\color{red}3}$ | $13$ |
$10\times 2 = {\color{green}20}$ | $3 \times 2 = {\color{red}6}$ | ${\color{green}20}+ {\color{red}6}$ | $26$ |
$10\times 3 = {\color{green}30}$ | $3 \times 3 = {\color{red}9}$ | ${\color{green}30} + {\color{red}9}$ | $39$ |
$10\times 4 = {\color{green}40}$ | $3 \times 4 = {\color{red}12}$ | ${\color{green}40}+ {\color{red}12}$ | $52$ |
$10\times 5 = {\color{green}50}$ | $3\times 5 = {\color{red}15}$ | ${\color{green}50} +{\color{red}15}$ | $65$ |
$10\times 6 = {\color{green}60}$ | $3\times 6 = {\color{red}18}$ | ${\color{green}60} +{\color{red}18}$ | $78$ |
$10\times 7 = {\color{green}70}$ | $3 \times 7 = {\color{red}21}$ | ${\color{green}70} +{\color{red}21}$ | $91$ |
$10\times 8 = {\color{green}80}$ | $3 \times 8 = {\color{red}24}$ | ${\color{green}80} + {\color{red}24}$ | $104$ |
$10\times 9 = {\color{green}90}$ | $3 \times 9 = {\color{red}27}$ | ${\color{green}90} + {\color{red}27}$ | $117$ |
$10\times 10 = {\color{green}100}$ | $3 \times 10 = {\color{red}30}$ | ${\color{green}100} + {\color{red}30}$ | $130$ |
Digits Pattern (Skipping Multiples of 4): This method is simple and effective in learning and memorizing the 13 times table. First, draw a table with three rows and three columns and write digits from 1 to 9 starting from the bottom left and moving upward, and ending at the top right cell, as shown in the table below. The digit zero is written separately.
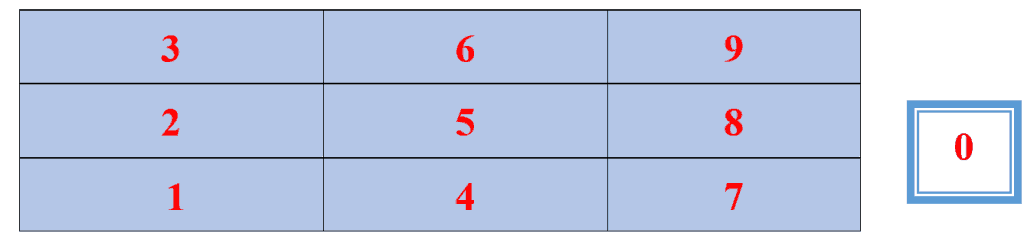
Now, write the natural numbers in ascending order while skipping the multiples of 4 (4, 8, and 12). The numbers should start from the top left and move to the right, ending at the bottom, right, as shown by the blue digits in the table below. The result is the 13 times table.
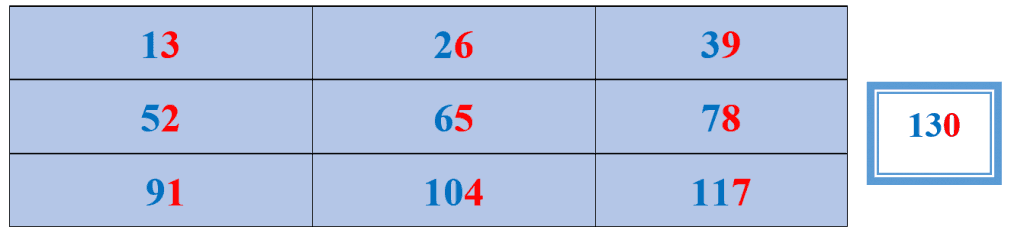
Table of 13 from 1 to 20:
A complete table of 13 from 1 to 20 can be written as:
Numerical Representation | Descriptive Representation | Product (Answer) |
$13 \times 1$ | Thirteen times one | $13$ |
$13 \times 2$ | Thirteen times two | $26$ |
$13 \times 3$ | Thirteen times three | $39$ |
$13 \times 4$ | Thirteen times four | $51$ |
$13 \times 5$ | Thirteen times five | $65$ |
$13 \times 6$ | Thirteen times six | $78$ |
$13 \times 7$ | Thirteen times seven | $91$ |
$13 \times 8$ | Thirteen times eight | $104$ |
$13 \times 9$ | Thirteen times nine | $117$ |
$13 \times 10$ | Thirteen times ten | $130$ |
$13 \times 11$ | Thirteen times eleven | $143$ |
$13 \times 12$ | Thirteen times twelve | $156$ |
$13 \times 13$ | Thirteen times thirteen | $169$ |
$13 \times 14$ | Thirteen times fourteen | $182$ |
$13 \times 15$ | Thirteen times fifteen | $195$ |
| $13 \times 16$ | Thirteen times sixteen | $208$ |
$13 \times 17$ | Thirteen times seventeen | $221$ |
$13 \times 18$ | Thirteen times eighteen | $234$ |
$13 \times 19$ | Thirteen times nineteen | $247$ |
$13 \times 20$ | Thirteen times twenty | $260$ |
Example 1: Calculate 13 times 3 minus 10 plus 5 times 13.
Solution:
13 times 3 minus 10 plus 5 times 13 can be written as:
$ = (13\times 3) – 10 + 5 \times 13$
$ = 39 – 10 + 65$
$ = 29 + 65 $
$ = 94$
Example 2: Calculate 13 times 13 times 10 minus 1000.
Solution:
13 times 13 times 10 minus 1000 can be written as:
$ = 13\times13 \times 10 – 1000$
$ = 169\times 10 – 1000$
$ = 1690 – 1000$
$ = 690$
Example 3: Sarah eats 5 bananas daily. How many bananas will she eat?
- In 13 days
- In 26 days
Solution:
- By using the 13 times table, we can calculate the number of bananas Sarah eats in 13 days.
$13 \times 5 = 65$ bananas
- We can also calculate the total number of bananas eaten in 26 days with the help of 13 times table.
We know that, $13 \times 2 = 26$. So, if we multiply the number of bananas eaten by Sarah in 13 days by ‘2’ we will get the total number of bananas she eats in 26 days, i.e., $65\times 2 = 130 $ bananas.
Example 4: Verify whether the eighth multiple of the number 13 is 114?
Solution:
We know the first 10 multiples of 13 are 13, 26, 39, 52, 65, 78, 91, 104, 117, and 130.
So, the eighth multiple of the number 13 is 104. Hence, 114 is not the eighth multiple of 13.
Example 5: Penny goes to a grocery store to purchase rice. The price of a kilogram of rice is 13 dollars. Penny has a total of 200 dollars; using the 13 times table calculate the remaining amount.
- If Penny purchases 7 kilograms of rice
- If Penny purchases 12 kilograms of rice
Solution:
- If Penny purchases 7 kilograms of rice, then the cost of rice can be calculated as:
$13\times 7 = 91$ dollars. If we subtract this amount from the total amount, we will get the remaining amount, i.e., $200 – 91 = 109$ dollars.
- If Penny purchases 7 kilograms of rice, then the cost of rice can be calculated as:
$13\times 12 = 156$ dollars.
Remaining amount $= 200 -156 = 44$ dollars.
Practice Questions:
- Alex has bought a new mobile phone in installments. The actual cost is 260 dollars, while Alex has to pay 13 dollars on a monthly basis. Calculate the total number of months for complete payment of the mobile.
- Jack saves 3 dollars from his pocket money daily. How much money will Jack have at the end of 13 days?
- Find the value of “Y” if “$ Y \times 13 = 13 \times 2 – 12 + 14 + 13 \times 3$.’’
- From the given table, select the numbers which are multiples of 13
| 24 | 38 | 18 | 21 | 51 | 269 | 182 |
| 41 | 34 | 74 | 96 | 19 | 240 | 111 |
| 48 | 72 | 98 | 94 | 99 | 104 | 211 |
| 120 | 131 | 49 | 121 | 118 | 113 | 47 |
| 159 | 260 | 216 | 52 | 114 | 112 | 61 |
| 09 | 14 | 13 | 79 | 86 | 89 | 134 |
| 91 | 73 | 71 | 179 | 65 | 215 | 195 |
| 99 | 156 | 154 | 99 | 151 | 208 | 138 |
| 221 | 84 | 77 | 51 | 227 | 96 | 266 |
| 64 | 68 | 55 | 59 | 160 | 220 | 270 |
Answer Key:
1) The mobile phone’s actual cost is 260 dollars, while Alex pays 13 dollars monthly. Using the 13 times table, we can calculate the total number of months Alex has to pay the installment.
$13 \times 20 =260$
So, Alex will have to pay 13 dollars for 20 months for the complete payment of the mobile phone.
2) At the end of 13 days, Jack will have $13\times 3 = 39$ dollars.
3) $ Y \times 13 = (13 \times 2) – 14 + 27 + (13 \times 3)$
$ Y \times 13 = 26 – 14 +27 + 39 $
$ Y \times 13 = 12 + 66 $
$ Y \times 13 = 78 $
We know $13 \times 6 =78$
$ Y = 6 $
4)
| 39 | 38 | 18 | 21 | 51 | 69 | 182 |
| 41 | 26 | 74 | 78 | 19 | 56 | 111 |
| 130 | 72 | 98 | 94 | 99 | 104 | 211 |
| 120 | 131 | 49 | 121 | 118 | 113 | 47 |
| 159 | 260 | 216 | 52 | 114 | 112 | 61 |
| 09 | 14 | 13 | 79 | 86 | 89 | 134 |
| 91 | 73 | 71 | 179 | 65 | 215 | 195 |
| 99 | 156 | 154 | 99 | 151 | 208 | 138 |
| 221 | 84 | 77 | 51 | 227 | 96 | 266 |
| 64 | 68 | 55 | 59 | 160 | 220 | 270 |
