JUMP TO TOPIC
15 Times Table – Explanation & Examples
The 15 Times Table is one of the easiest multiplication tables to learn and memorize. The number 15 has three divisors, 1, 3, and 5, and it is often used in solving mathematical problems related to multiplications, fractions, division, L.C.M, and H.C.F.
The 15 times table is a table that contains the multiples of the number 15.
The 15 times table is quite easy as it follows a simple pattern of digits. We will provide interesting tips and tricks to learn and understand the 15 times table.
You should refresh the following concepts to understand the material discussed here.
- Basics of addition and multiplication
- Maths Table of 1 to 14
15 Multiplication Table
The table of 15 can be written as:
- $15 \times1 = 15$
- $15 \times 2 = 30$
- $15 \times 3 = 45$
- $15 \times 4 =60$
- $15 \times 5 =75$
- $15 \times 6 =90$
- $15 \times 7 = 105$
- $15 \times 8 = 120$
- $15 \times 9 = 135$
- $15 \times 10 = 150$
Different Tips for the 15 Times Table:
Let us look at some simple tips which can help you memorize the 15 times table.
Using the 10 and the 5 Times Tables is one of the simplest methods to learn the 15 times tables. It requires the usage of the 10 and the 5 times tables that are quite easy to memorize. If we add the multiples of the number 10 to the multiples of the number 5, the outcome will be the multiples of the number 15. For example, the eighth multiple of the number 10 is 80, and the eighth multiple of the number 5 is 40, and if we add 80 and 40, we get 120 which is the eighth multiple of the number 15. The detailed method is presented in the table below.
10 Times Table | 5 Times Table | Addition | Outcome |
$10\times 1 = {\color{green}10}$ | $ 5 \times 1 = {\color{red}5}$ | ${\color{green}10}+ {\color{red}5}$ | $15$ |
$10\times 2 = {\color{green}20}$ | $5 \times 2 = {\color{red}10}$ | ${\color{green}20}+ {\color{red}10}$ | $30$ |
$10\times 3 = {\color{green}30}$ | $5 \times 3 = {\color{red}15}$ | ${\color{green}30} + {\color{red}15}$ | $45$ |
$10\times 4 = {\color{green}40}$ | $5 \times 4 = {\color{red}20}$ | ${\color{green}40}+ {\color{red}20}$ | $60$ |
$10\times 5 = {\color{green}50}$ | $5\times 5 = {\color{red}25}$ | ${\color{green}50} +{\color{red}25}$ | $75$ |
$10\times 6 = {\color{green}60}$ | $5\times 6 = {\color{red}30}$ | ${\color{green}60} +{\color{red}30}$ | $90$ |
$10\times 7 = {\color{green}70}$ | $5 \times 7 = {\color{red}35}$ | ${\color{green}70} +{\color{red}35}$ | $105$ |
$10\times 8 = {\color{green}80}$ | $5 \times 8 = {\color{red}40}$ | ${\color{green}80} + {\color{red}40}$ | $120$ |
$10\times 9 = {\color{green}90}$ | $5 \times 9 = {\color{red}45}$ | ${\color{green}90} + {\color{red}45}$ | $135$ |
$10\times 10 = {\color{green}100}$ | $5 \times 10 = {\color{red}50}$ | ${\color{green}100} + {\color{red}50}$ | $150$ |
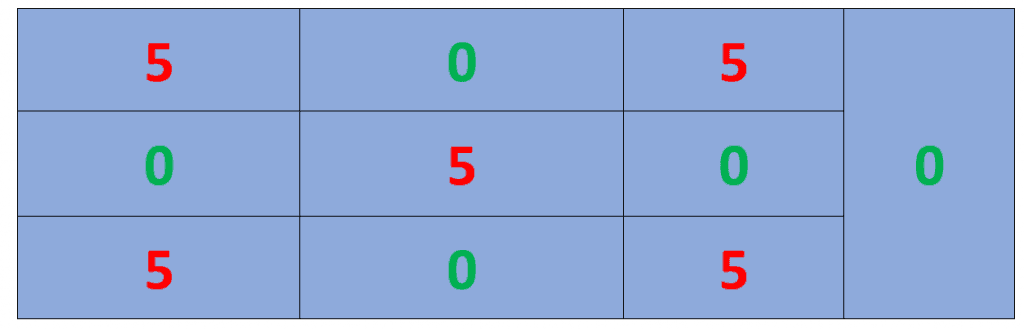
Using Odd and Even Numbers Pattern: This method is a little tricky, but once you get the hang of it, you will learn the 15 times table in no time. Draw a 3 x 3 grid and add a merged tenth cell as shown below. Now, write the digit 5 in the top-left cell and the digit 0 in the next cell and repeat this process until you fill the last cell of the grid. The final shape of the table is shown in the picture below.
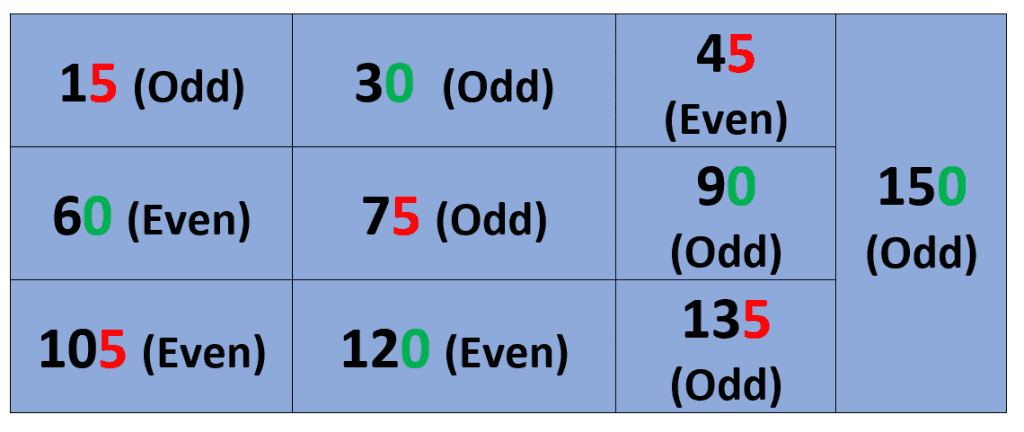
Start from the top-left cell and write the first two odd numbers, 1 and 3, as shown in the picture below. In the third and fourth cells of the grid, write the two even digits after the number 3. Similarly, in the next two cells, you write two odd digits and then two even digits and so on. So, the pattern we have is two odd (1 and 3), two even ( 4 and 6) again two odds (7 and 9), then two even (10 and 12), and finally two odds (13 and 15), as shown in the picture below. The table now contains the first ten multiples of 15.
Addition: The addition method can also be used to learn and memorize the 15 times table. If you are having difficulty understanding the previous tips, you can use this as a starter method to help you understand the 15 times table, and it will also help you strengthen your addition skills. As the name suggests, this method involves the simple addition of the number 15. For example, we start with the digit 0, and if we add the number 15 to it, we get 15 as an answer. Similarly, if we add 15 to 15, then the outcome will be 30, and so on. The method is represented in the picture below.
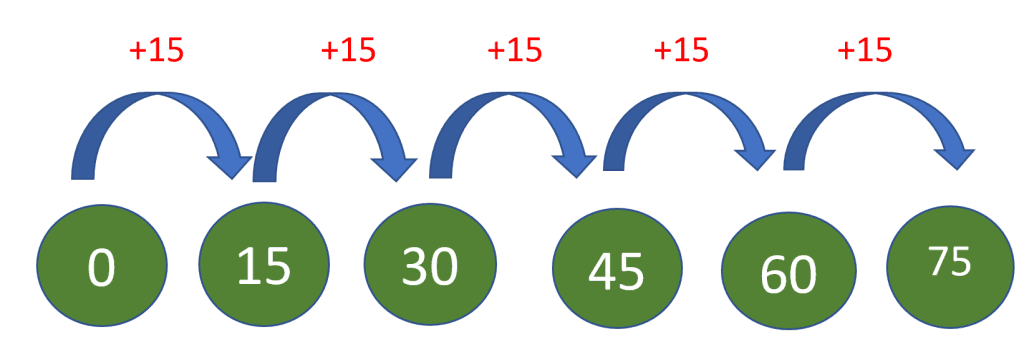
Table of 15 from 1 to 20:
A complete table of 15 from 1 to 20 can be written as:
Numerical Representation | Descriptive Representation | Product (Answer) |
$15 \times 1$ | Fifteen times one | $15$ |
$15 \times 2$ | Fifteen times two | $30$ |
$15 \times 3$ | Fifteen times three | $45$ |
$15 \times 4$ | Fifteen times four | $60$ |
$15 \times 5$ | Fifteen times five | $75$ |
$15 \times 6$ | Fifteen times six | $90$ |
$15 \times 7$ | Fifteen times seven | $105$ |
$15 \times 8$ | Fifteen times eight | $120$ |
$15 \times 9$ | Fifteen times nine | $135$ |
$15\times 10$ | Fifteen times ten | $150$ |
$15 \times 11$ | Fifteen times eleven | $165$ |
$15 \times 12$ | Fifteen times twelve | $180$ |
$15 \times 13$ | Fifteen times thirteen | $195$ |
$15 \times 14$ | Fifteen times fourteen | $210$ |
$15 \times 15$ | Fifteen times fifteen | $225$ |
$15 \times 16$ | Fifteen times sixteen | $240$ |
$15 \times 17$ | Fifteen times seventeen | $255$ |
$15 \times 18$ | Fifteen times eighteen | $270$ |
$15 \times 19$ | Fifteen times nineteen | $285$ |
| $15 \times 20$ | Fifteen times twenty | $300$ |
Example 1: Allan goes to a shopping mall to buy new dresses for his daughters. Allan wants to buy seven new dresses, and the cost of each dress is 15 dollars. Allan has 100 dollars in his wallet. Using the 15 times table, can you tell whether or not Allan has sufficient money to buy seven dresses?
Solution:
The cost of each dress is 15 dollars. So, by using the 15 times table, we can calculate the total cost of seven dresses as,
$15\times 7 = 105$ dollars
The total cost of seven dresses is 105 dollars while Allan has 100 dollars. So, Allan needs 5 more dollars to buy all the dresses.
Example 2: Calculate 15 times 3 times 10 minus 200?
Solution:
15 times 3 times 10 minus 200 can be written as:
$ = (15\times 3 \times 10) – 200$
$ = (45\times 10) – 200$
$ = 450 – 200$
$ = 250$
Example 3: Calculate 15 times 13 plus 90 minus 15 times 9?
Solution:
15 times 13 plus 90 minus 15 times 9 can be written as:
$ = (15\times 13) +90 – (15\times 9)$
$ = (195) +90 – (15\times 9)$
$ = 195 + 70 – 135$
$ = 265 – 135$
$ = 130$
Example 4: Darren loves to collect different stamps, and he has a pouch that can contain 15 stamps at maximum. Calculate the total number of stamps collected by Darren.
- If he has 8 pouches
- If he has 15 pouches
- If he has 18 pouches
Solution:
- If Darren has 8 pouches, the total number of stamps can be calculated as $15 \times 8 = 120$.
- If Darren has 15 pouches, the total number of stamps can be calculated as $15 \times 15 = 225$.
- If Darren has 18 pouches, the total number of stamps can be calculated as $15 \times 18 = 270$.
Practice Questions:
- Sherry is studying in grade 2, and the total number of students in her class is 15. It is her birthday, and she wants to give five candies to each of her class fellows. Can you calculate the total number of candies Sherry needs to buy for her class?
- What is the 9th multiple of 15?
- From the given table, select the numbers which are multiples of 15
| 130 | 137 | 135 | 160 | 150 | 51 | 61 | 180 |
| 125 | 19 | 20 | 18 | 10 | 300 | 167 | 154 |
| 190 | 11 | 113 | 117 | 100 | 73 | 99 | 321 |
| 151 | 30 | 14 | 116 | 15 | 104 | 133 | 129 |
| 110 | 111 | 200 | 25 | 21 | 187 | 141 | 210 |
| 132 | 141 | 105 | 29 | 70 | 88 | 129 | 220 |
| 240 | 321 | 119 | 34 | 35 | 169 | 160 | 219 |
| 109 | 120 | 260 | 39 | 80 | 100 | 250 | 231 |
| 41 | 165 | 43 | 151 | 45 | 122 | 214 | 257 |
| 44 | 43 | 280 | 49 | 75 | 132 | 215 | 109 |
Answer Key:
1). You can calculate the total number of candies Sherry needs to buy by using the 15 times table.
$15\times 5 =105$ candies. So, if Sherry buys 105 candies, she can distribute five candies to each of her class fellows.
2). First 10 multiples of 15 can be written as: 15,30,45, 60, 75, 90, 105, 120, 135 and 150
So, the ninth multiple is 135.
3).
| 130 | 137 | 135 | 160 | 150 | 51 | 61 | 180 |
| 125 | 19 | 20 | 18 | 10 | 300 | 167 | 154 |
| 190 | 11 | 113 | 117 | 100 | 73 | 99 | 321 |
| 151 | 30 | 14 | 116 | 15 | 104 | 133 | 129 |
| 110 | 111 | 200 | 25 | 21 | 187 | 141 | 210 |
| 132 | 141 | 105 | 29 | 70 | 88 | 129 | 220 |
| 240 | 321 | 119 | 34 | 35 | 169 | 160 | 219 |
| 109 | 120 | 260 | 39 | 80 | 100 | 250 | 231 |
| 41 | 165 | 43 | 151 | 45 | 122 | 214 | 257 |
| 44 | 43 | 280 | 49 | 75 | 132 | 215 | 109 |