JUMP TO TOPIC
16 Times Table – Explanation & Examples
The 16 times table is the multiplication table of the number 16, and it is generated by multiplying the number 16 with natural numbers. There are no simple rules for the 16 times table, which makes it slightly difficult to learn and memorize. On the other hand, if you learn the 16 times table, it will help you solve complex multiplication and division-related problems.
16 times table is a table that contains the multiples of the number 16.
In this topic, we will present some tips and patterns that will help you learn and memorize the 16 times table.
You should refresh the following concepts to understand the material discussed here.
- Basics of addition and multiplication.
- 6 times table.
- 8 times table.
- 10 times table.
16 Multiplication Table
The table of 16 can be written as:
- $16 \times 1 = 16$
- $16 \times 2 = 32$
- $16 \times 3 = 48$
- $16 \times 4 =64$
- $16 \times 5 =80$
- $16 \times 6 =96$
- $16 \times 7 = 112$
- $16 \times 8 = 128$
- $16 \times 9 = 144$
- $16 \times 10 = 160$
Different Tips for 16 Times Table:
Let us look at some simple tips which can help you memorize the 16 times table.
Digits Pattern: Just like the 4, 8, and 12 times table, the 16 times table follows a digit pattern of five multiples. Note that all the tables of the multiples of 4 have a digit pattern that repeats itself after 5 multiples. In the 16 times table pattern, the ten’s digits of the first five multiples are 6,2,8,4 and 0. The same sequence is repeated for the next five multiples and so on. The pattern is shown in the table below.
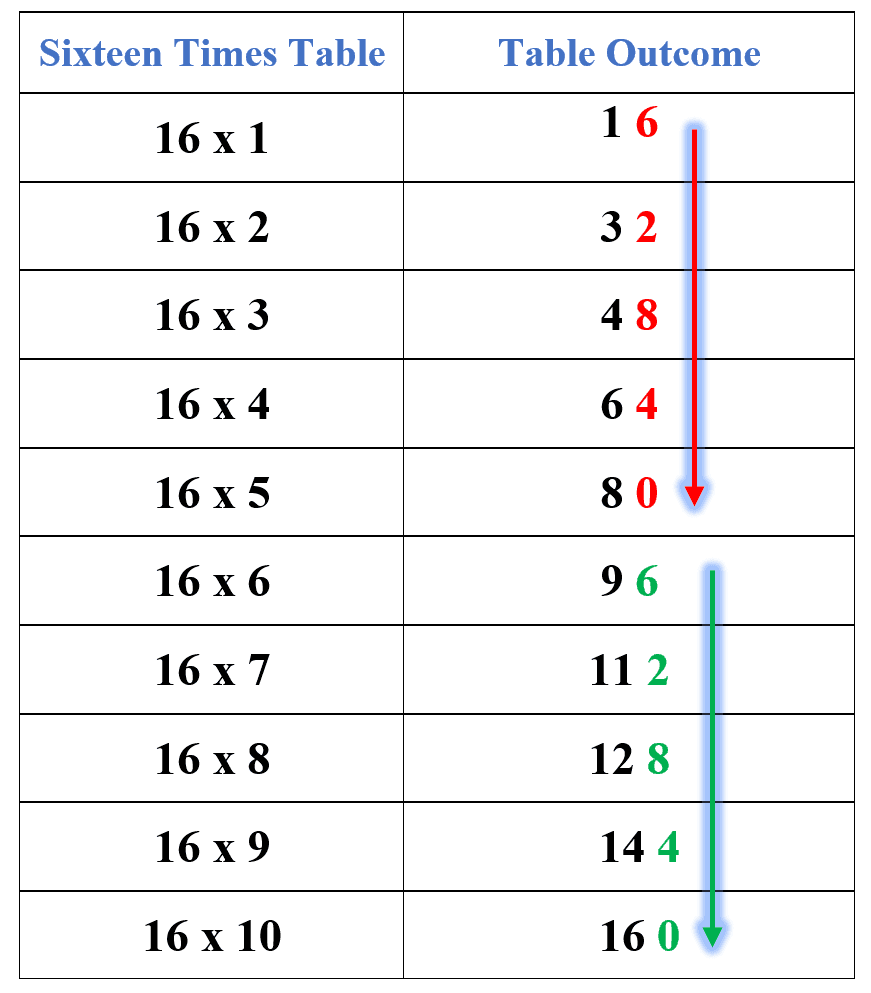
Using the 10 and the 6 Times Tables: This is one of the easiest methods to learn the 16 times tables. It requires the usage of the 10 and the 6 times tables, which also helps in revising these tables. If we add the multiples of 10 times table to the multiples of 6 times table, the results are multiples of the 6 times table. For example, the second multiple of 10 is 20, and the second multiple of 6 is 12, and if we add 20 and 12, we get 32 which is the second multiple of 16. The detailed method is presented in the table below.
Ten Times Table | Six Times Table | Addition | Outcome |
$10\times 1 = {\color{green}10}$ | $ 6 \times 1 = 6$ | ${\color{green}10}+ {\color{red}6}$ | $16$ |
$10\times 2 = {\color{green}20}$ | $6 \times 2 = 12$ | ${\color{green}20}+ {\color{red}12}$ | $32$ |
$10\times 3 = {\color{green}30}$ | $6 \times 3 = 18$ | ${\color{green}30} + {\color{red}18}$ | $48$ |
$10\times 4 = {\color{green}40}$ | $6 \times 4 = 24$ | ${\color{green}40}+ {\color{red}24}$ | $64$ |
$10\times 5 = {\color{green}50}$ | $6\times 5 = 30$ | ${\color{green}50} +{\color{red}30}$ | $80$ |
$10\times 6 = {\color{green}60}$ | $6\times 6 = 36$ | ${\color{green}60} +{\color{red}36}$ | $96$ |
$10\times 7 = {\color{green}70}$ | $6 \times 7 = 42$ | ${\color{green}70} +{\color{red}42}$ | $112$ |
$10\times 8 = {\color{green}80}$ | $6 \times 8 = 48$ | ${\color{green}80} + {\color{red}48}$ | $128$ |
$10\times 9 = {\color{green}90}$ | $6 \times 9 = 54$ | ${\color{green}90} + {\color{red}54}$ | $144$ |
$10\times 10 = {\color{green}100}$ | $6 \times 10 = 60$ | ${\color{green}100} + {\color{red}60}$ | $160$ |
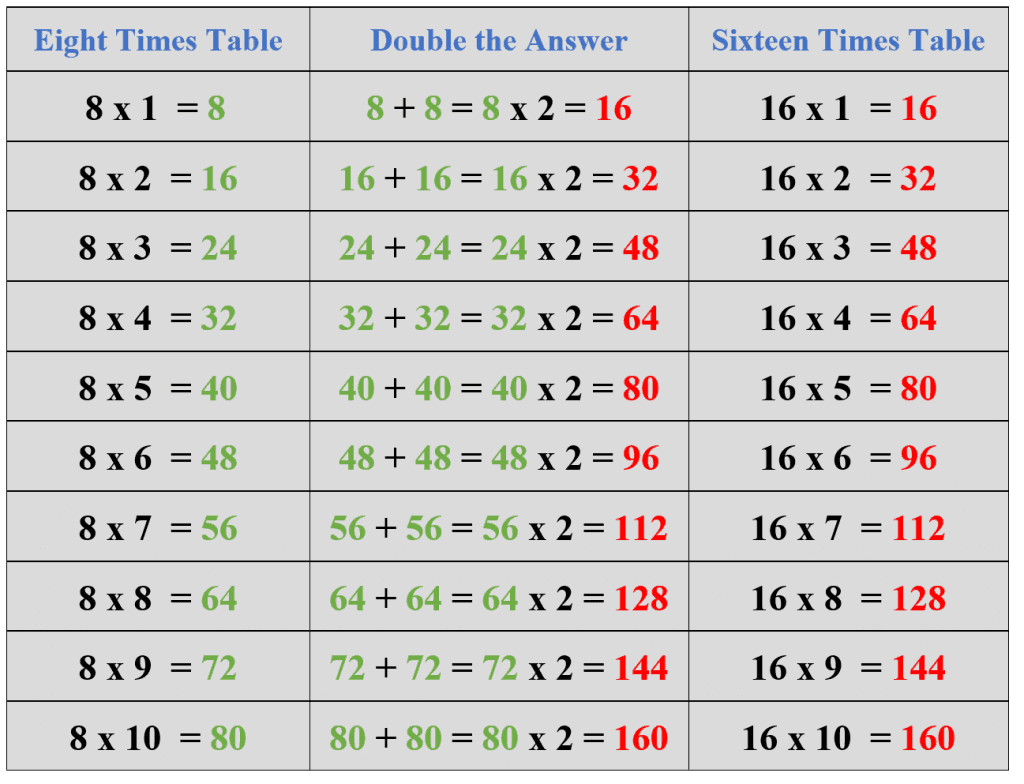
Using the 8 Times Table: The 8 times table can be used to learn and memorize 16 times table. This method is very effective if you have already memorized the 8 times table. The 8 times table can be used in two different methods to help you memorize the 16 times table.
- First Method: You need to write the 8 times table up to the first 10 multiples in the first method. Then if we double the value of a multiple or add the multiple to itself, the result will be a multiple of 16. For example, the third multiple of 8 is 24; if we double its value, i.e., $24\times2 = 48$, or add the multiple to itself, i.e., $24+24 = 48$, the answer 48 is the third multiple of the number 16. The detailed method is presented below in the table.
- Second Method: In the second method, you write the 8 times table up to the first 20 multiples. If you highlight all the even multiples from top to bottom, these multiples will form a 16 times table of the first 10 multiples of 16. For example, the fourth multiple of 8 is 32 which is also the second multiple of 16. This method is presented in the table below.
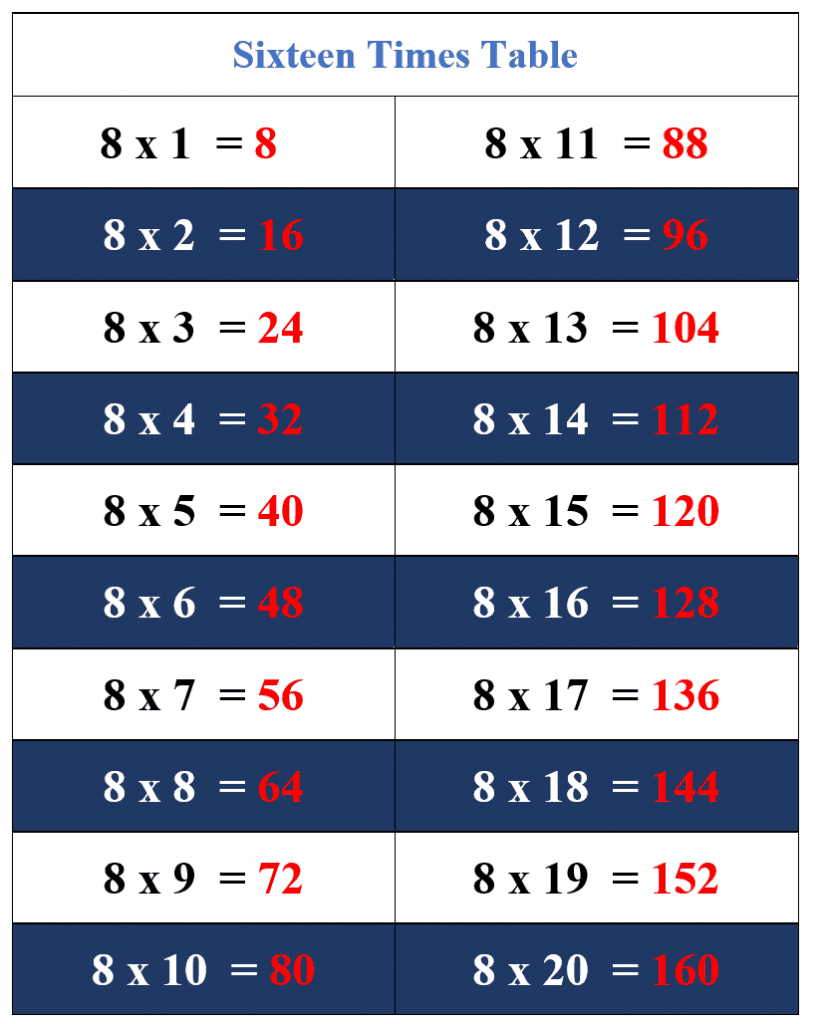
Table of 16 from 1 to 20:
A complete table of 16 from 1 to 20 can be written as:
Numerical Representation | Descriptive Representation | Product (Answer) |
$16 \times 1$ | Sixteen times one | $16$ |
$16 \times 2$ | Sixteen times two | $32$ |
$16 \times 3$ | Sixteen times three | $48$ |
$16 \times 4$ | Sixteen times four | $64$ |
$16 \times 5$ | Sixteen times five | $80$ |
$16 \times 6$ | Sixteen times six | $96$ |
$16 \times 7$ | Sixteen times seven | $112$ |
$16 \times 8$ | Sixteen times eight | $128$ |
$16 \times 9$ | Sixteen times nine | $144$ |
$16 \times 10$ | Sixteen times ten | $160$ |
$16 \times 11$ | Sixteen times eleven | $176$ |
$16 \times 12$ | Sixteen times twelve | $192$ |
$16 \times 13$ | Sixteen times thirteen | $208$ |
$16 \times 14$ | Sixteen times fourteen | $224$ |
$16 \times 15$ | Sixteen times fifteen | $240$ |
$16 \times 16$ | Sixteen times sixteen | $256$ |
$16 \times 17$ | Sixteen times seventeen | $272$ |
$16 \times 18$ | Sixteen times eighteen | $288$ |
| $16 \times 19$ | Sixteen times nineteen | $304$ |
$16 \times 20$ | Sixteen times twenty | $320$ |
Example 1: Calculate 16 times 9 minus 100 plus 50.
Solution:
16 times 9 minus 100 plus 50 can be written as:
$ = (16\times 9) – 100 + 50$
$ = 144 – 50 $
$ = 94$
Example 2: Calculate 16 times 11 minus 150 plus 10 times 16.
Solution:
16 times 11 minus 150 plus 10 times 16 can be written as:
$ = 16\times11 – 150 + 10\times 16$
$ = 276 – 150 + 160$
$ = 126 + 160$
$ = 286$
Example 3: Alexander has 10 dozen oranges in his shop. Calculate the number of remaining oranges at the end of the week
- If Alexander sells 16 oranges daily for 5 days
- If Alexander sells 16 oranges daily for a week
Solution:
We know that 1 dozen is = 12, so 6 dozen $= 10 \times 12 = 120$
- If Alexander sells 16 oranges daily for 5 days, then by using the 16 times table we can calculate the number of remaining oranges as:
$16 \times 5 = 80$ oranges.
Remaining oranges $= 120 – 80 = 40$ oranges
- If Alexander sells 16 oranges daily for a week, then by using the 16 times table, we can calculate the number of remaining oranges as:
$16 \times 7 = 112$ oranges.
Remaining oranges $= 120 – 112 = 8$ oranges.
Example 4: Verify whether the seventh multiple of the number 16 is 112 or not?
Solution:
We know the first 10 multiples of 16 are 16, 32, 48, 64, 80, 96, 112, 128, 144, and 160.
Hence, 112 is the seventh multiple of 16.
Practice Questions:
- Allan bought a new camera. The camera has a special feature, i.e., if you press the capture button, the camera takes 16 pictures simultaneously. Calculate the total number of pictures taken if Allan pressed the capture button 8 times.
- Find the value of “Y” if “$ Y \times 16 = 16 \times 8 + 18 – 4\times 16$.’’
- Calculate 3 times 2 times 2 times 16 minus 100
- From the given table, select the numbers which are multiples of 16
| 142 | 138 | 18 | 210 | 240 | 69 | 182 |
| 141 | 26 | 14 | 78 | 219 | 56 | 111 |
| 130 | 172 | 16 | 96 | 230 | 104 | 211 |
| 120 | 131 | 59 | 121 | 118 | 113 | 47 |
| 320 | 280 | 216 | 52 | 114 | 144 | 61 |
| 309 | 314 | 32 | 79 | 86 | 89 | 134 |
| 360 | 73 | 71 | 179 | 65 | 215 | 195 |
| 336 | 156 | 154 | 99 | 151 | 208 | 138 |
| 121 | 80 | 77 | 51 | 227 | 96 | 266 |
| 64 | 68 | 55 | 59 | 160 | 220 | 272 |
Answer Key:
1) The total number of pictures can be calculated by using the 16 times table.
Allan pressed the capture button 8 times, so the total number of pictures taken by the camera is $16\times 8 = 128$.
2) $ Y \times 16 = 16 \times 8 + 16 – 4\times 16$.
$ Y \times 16 = 128 + 16 – 64 $.
$ Y \times 16 = 144 – 64 $.
$ Y \times 16 = 80 $.
We know $16 \times 5 =80$, so
$ Y = 5 $.
3). 3 times 2 times 2 times 16 minus 100 can be written as:
$ = (3\times 2 \times 2 \times 16) – 100$
$ = (6 \times 2 \times 16) – 100$
$ = (12 \times 16) – 100$
$ = 192 – 100$
$ = 92$
4)
| 142 | 138 | 18 | 210 | 240 | 69 | 182 |
| 141 | 26 | 14 | 78 | 219 | 56 | 111 |
| 130 | 172 | 16 | 96 | 230 | 104 | 211 |
| 120 | 131 | 59 | 121 | 118 | 113 | 47 |
| 320 | 280 | 216 | 52 | 114 | 144 | 61 |
| 309 | 314 | 32 | 79 | 86 | 89 | 134 |
| 360 | 73 | 71 | 179 | 65 | 215 | 195 |
| 336 | 156 | 154 | 99 | 151 | 208 | 138 |
| 121 | 80 | 77 | 51 | 227 | 96 | 266 |
| 64 | 68 | 55 | 59 | 160 | 220 | 272 |