JUMP TO TOPIC
20 Times Table – Explanation & Examples
The 20 times table is one of the most commonly used tables in solving mathematical problems related to fractions, divisions, L.C.M, H.C.F, and multiplications. It is also one of the easiest tables to learn and memorize.
20 times table is a table that contains the multiples of the number 20.
We will provide interesting tips and skills to learn and understand the 20 times table.
You should refresh the following concepts to understand the material discussed here.
- Basics of addition and multiplication
- 10 multiplication table
20 Multiplication Table
The table of 20 can be written as:
- $20\times1 = 20$
- $20 \times 2 = 40$
- $20 \times 3 = 60$
- $20 \times 4 =80$
- $20 \times 5 =100$
- $20\times 6 =120$
- $20\times 7 = 140$
- $20\times 8 = 160$
- $20\times 9 = 180$
- $20\times 10 = 200$
Different Tips for the 20 Times Table:
The 20 times table is easy to understand and memorize if you know the tips and tricks. Let us look at some of these tips.
- Adding Zero at the End of Even Numbers: This is the golden method to help you memorize the 20 times table. First, draw a 3 x 3 grid and then write the even numbers ascending from top left to bottom-right, as shown by the red digits in the picture below. The number 20 can be written in a separate cell or add a 10th cell to the 3 x 3 grid.
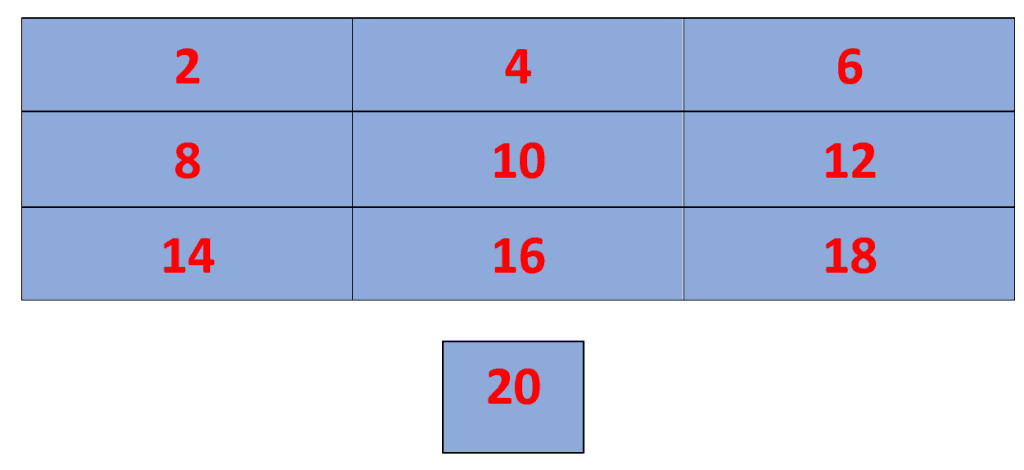
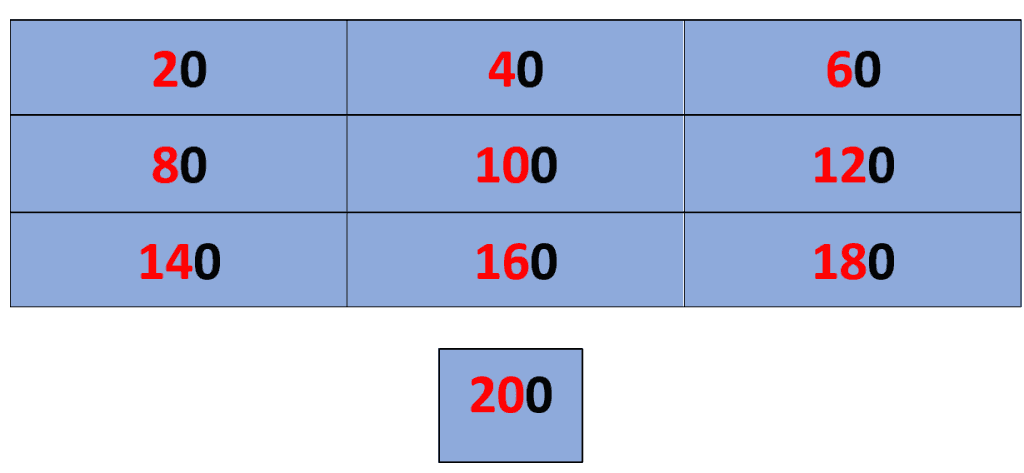
Once you have written all the even digits, add zeros at the end of each red number, and you will get multiples of the number 20 in ascending order. For example, the first even number is “2” if we add “0” at the end, we get 20 which is the first multiple of the number 20. Similarly, the sixth even number is “12” if we add “0” at the end, we get 120 which is the sixth multiple of the number 20. The method is shown in the table below.
Using the 10 times table: The above method we just discussed is sufficient for learning and memorizing the 20 times table. However, if you want to revise the 10 times table and test your addition and multiplication skills, then you can also use the 10 times table to help you learn and memorize the 20 times table. In this method, the outcomes of the 10 times table are doubled, i.e., by multiplying by “2” or adding the answer to itself. For example, $10\times 6 = 60$ and if we multiply 60 by “2” or add 60 + 60, we get 120 which is the sixth multiple of the number 20.
| 10 Times Table | Double the Answer | 20 Times Table |
| $10\times 1 = {\color{green}10}$ | ${\color{green}10} + {\color{green}10} = {\color{red}20}$ | $20\times 1 = {\color{green}20}$ |
| $10\times 2 = {\color{green}20}$ | ${\color{green}20} + {\color{green}20} = {\color{red}40}$ | $20\times 2 = {\color{green}48}$ |
| $10\times 3 = {\color{green}30}$ | ${\color{green}30} + {\color{green}30} = {\color{red}60}$ | $20\times 3 = {\color{green}72}$ |
| $10\times 4 = {\color{green}40}$ | ${\color{green}40} + {\color{green}40} = {\color{red}80}$ | $20\times 4 = {\color{green}96}$ |
| $10\times 5 = {\color{green}50}$ | ${\color{green}50} + {\color{green}50} = {\color{red}100}$ | $20\times 5 = {\color{green}120}$ |
| $10\times 6 = {\color{green}60}$ | ${\color{green}60} + {\color{green}60} = {\color{red}120}$ | $20\times 6 = {\color{green}144}$ |
| $10\times 7 = {\color{green}70}$ | ${\color{green}70} + {\color{green}70} = {\color{red}140}$ | $20\times 7 = {\color{green}168}$ |
| $10\times 8 = {\color{green}80}$ | ${\color{green}80} + {\color{green}80} = {\color{red}160}$ | $20\times 8 = {\color{green}192}$ |
| $10\times 9 = {\color{green}90}$ | ${\color{green}90} + {\color{green}90} = {\color{red}180}$ | $20\times 9 = {\color{green}216}$ |
| $10\times 10 = {\color{green}100}$ | ${\color{green}100} + {\color{green}100} = {\color{red}200}$ | $20\times 10 = {\color{green}240}$ |
- Addition: This method can also be utilized to learn and understand the 20 times table, and it will help you strengthen your addition skills as well. As the name suggests, this method involves simple addition. For example, we start with the digit 0, and if we add the number 20 to it, we get 20 as an answer. Similarly, if we add 20 to 20, the outcome is 40, which is the second multiple of 20. This way, we can work out the next multiples of the number 20 by adding 20 to the previous answer and so on, as shown in the picture below.
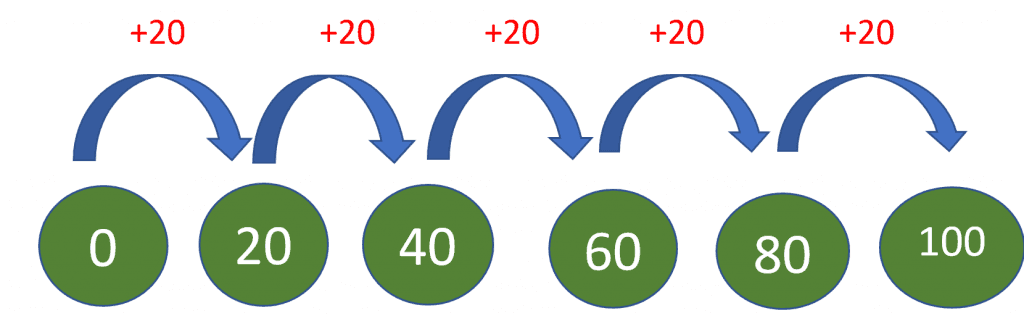
Table of 20 from 1 to 20:
A complete table of 20 from 1 to 20 can be written as:
Numerical Representation | Descriptive Representation | Product (Answer) |
$20 \times 1$ | Twenty times one | $20$ |
$20 \times 2$ | Twenty times two | $40$ |
$20 \times 3$ | Twenty times three | $60$ |
$20 \times 4$ | Twenty times four | $80$ |
$20 \times 5$ | Twenty times five | $100$ |
$20 \times 6$ | Twenty times six | $120$ |
$20 \times 7$ | Twenty times seven | $140$ |
$20 \times 8$ | Twenty times eight | $160$ |
$20 \times 9$ | Twenty times nine | $180$ |
$20 \times 10$ | Twenty times ten | $200$ |
$20 \times 11$ | Twenty times eleven | $220$ |
$20 \times 12$ | Twenty times twelve | $240$ |
$20 \times 13$ | Twenty times thirteen | $260$ |
$20 \times 14$ | Twenty times fourteen | $280$ |
$20 \times 15$ | Twenty times fifteen | $300$ |
$20 \times 16$ | Twenty times sixteen | $320$ |
$20 \times 17$ | Twenty times seventeen | $340$ |
$20 \times 18$ | Twenty times eighteen | $360$ |
$20 \times 19$ | Twenty times nineteen | $380$ |
$20 \times 20$ | Twenty times twenty | $400$ |
Example 1: Calculate 2 times 3 times 20 minus 70
Solution:
2 times 3 times 20 minus 70 can be written as:
$ = (2\times 3 \times 20) – 70$
$ = 6\times 20 – 70$
$ = 120 – 70 $
$ = 50 $
Example 2: Andy has to travel 10 kilometers daily to reach his workplace, and he takes the same route to get back home. What will be the total distance covered by Andy? Also, calculate the total distance covered by Andy in
- 7 days
- 11 days
- 15 days
Solution:
Andy travels 10 kilometers on the route to the office, and he travels 10 kilometers on his route back. So, the total distance covered by Andy daily is 10 +10 = 20 kilometers.
- We can calculate the total distance covered by Andy in 7 days by using the 20 times table, i.e., $20\times 7 = 140$ kilometers.
- The distance covered in 11 days is $20\times 11 = 220$ kilometers.
- The distance covered in 15 days is $20\times 15 = 300$ kilometers.
Example 3: Calculate 20 times 10 plus 70 minus 20 times 9?
Solution:
20 times 10 plus 70 minus 20 times 9 can be written as:
$ = (20\times 10) +70 – (20\times 9)$
$ = (200) +70 – (20\times 9)$
$ = 200 + 70 – 180$
$ = 270 – 180$
$ = 90$
Example 4: George is working as a laborer on daily wages, and he earns 30 dollars a day. If George’s daily expenses are 20 dollars, then calculate the total expenditure and the amount saved by George at the end of
- 10 days.
- 15 days.
- 20 days
Solution:
- We can calculate the total expenditure by using the 20 times table. The total expenses of George in 10 days is $20\times 10 = 200$ dollars. George earns 30 dollars a day, and his expense is 20 dollars, so daily saving is $30 – 20 = 10$ dollars. So, the total amount saved can be calculated using the 10 times table, i.e., $10\times 10 = 100$ dollars.
- Total expenditure in 15 days can be calculated as $20\times 15 = 300$ dollars. Total amount saved is $10\times 15 = 150$ dollars.
- Total expenditure in 20 days can be calculated as $20\times 20 = 400$ dollars. Total amount saved is $10\times 15 = 150$ dollars.
Practice Questions:
- David and Chris are playing a quiz-based game. For each question, the correct answer is equal to 20 points. The person who scores 300 points first will win the game. Using the 20 times table, calculate the total number of correct answers needed to win the game.
- Subtract the sum of the first 10 even multiples of the number 20 from the first 10 odd multiples of the number 20.
- Calculate 20 times 20 times 10 minus 1000?
- From the given table, select the numbers which are multiples of 20
| 187 | 137 | 16 | 160 | 50 | 51 | 61 | 880 |
| 225 | 19 | 20 | 18 | 10 | 300 | 67 | 154 |
| 90 | 11 | 13 | 17 | 400 | 403 | 99 | 321 |
| 15 | 230 | 14 | 16 | 30 | 104 | 33 | 129 |
| 310 | 295 | 200 | 25 | 21 | 87 | 41 | 210 |
| 332 | 14 | 55 | 29 | 70 | 88 | 29 | 220 |
| 440 | 32 | 39 | 34 | 35 | 69 | 360 | 219 |
| 410 | 120 | 360 | 39 | 80 | 100 | 350 | 231 |
| 41 | 65 | 43 | 51 | 45 | 122 | 214 | 257 |
| 44 | 43 | 680 | 49 | 80 | 132 | 215 | 109 |
Answer Key:
1) By using the 20 times table, we know that,
$20\times 15 =300$ points
So, the first person to guess 15 correct answers will win the game.
2) We know the first 10 odd multiples of 20 are 20, 60, 100, 140, 180, 220, 260, 300, 340, and 380.
The first 10 even multiples of 20 are 40, 80, 120, 160, 200, 240, 280 320, 360, and 400.
Sum of all the odd multiples of the number 20 is $20 + 60 + 100 + 140 + 180 + 220 + 260 + 300 + 340 + 380 = 2000$.
Sum of all the even multiples of the number 20 is $40 + 80 + 120 + 160 + 200 + 240 + 280 + 320 + 360 + 400 = 2200$.
The difference between the sum of even and odd multiples is $= 2200 – 2000 = 200$.
3) 20 times 20 times 10 minus 3000 can be written as:
$ = (20\times 200 \times 10) -3000$
$ = (400 \times 10) -3000$
$ = 4000 – 3000$
$ = 1000$
4)
| 187 | 137 | 16 | 160 | 50 | 51 | 61 | 880 |
| 225 | 19 | 20 | 18 | 10 | 300 | 67 | 154 |
| 90 | 11 | 13 | 17 | 400 | 403 | 99 | 321 |
| 15 | 230 | 14 | 16 | 30 | 104 | 33 | 129 |
| 310 | 295 | 200 | 25 | 21 | 87 | 41 | 210 |
| 332 | 14 | 55 | 29 | 70 | 88 | 29 | 220 |
| 440 | 32 | 39 | 34 | 35 | 69 | 360 | 219 |
| 410 | 120 | 360 | 39 | 80 | 100 | 350 | 231 |
| 41 | 65 | 43 | 51 | 45 | 122 | 214 | 257 |
| 44 | 43 | 680 | 49 | 80 | 132 | 215 | 109 |