• Home
  • >
  • 21 Times Table – Explanation & Examples

21 Times Table – Explanation & Examples

21 Times TableThe 21 times table is the multiplication table of the number 21. Learning the 21 times table is essential for solving fractions, divisions, L.C.M, H.C.F, and multiplications.

The 21 times table is a table that contains the multiples of the number 21.

In this topic, we will provide exciting tips and patterns to help you learn and memorize the 21 times table quickly and easily.

You should refresh the following concepts to understand the material discussed on this topic.

  1. Basics of addition and multiplication
  2. Maths table of 1 to 20

21 Multiplication Table

The table of 21 can be written as:

  • $21 \times 1 = 21$
  • $21 \times 2 = 42$
  • $21 \times 3 = 63$
  • $21 \times 4 =84$
  • $21 \times 5 =105$
  • $21 \times 6 =126$
  • $21 \times 7 = 147$
  • $21 \times 8 = 168$
  • $21 \times 9 = 189$
  • $21 \times 10 = 210$

Different Tips for the 21 Times Table:

The 21 times table is easy to understand and memorize if you know the tips and tricks. Let us look at some of these simple techniques which can help you memorize the 21 times table.

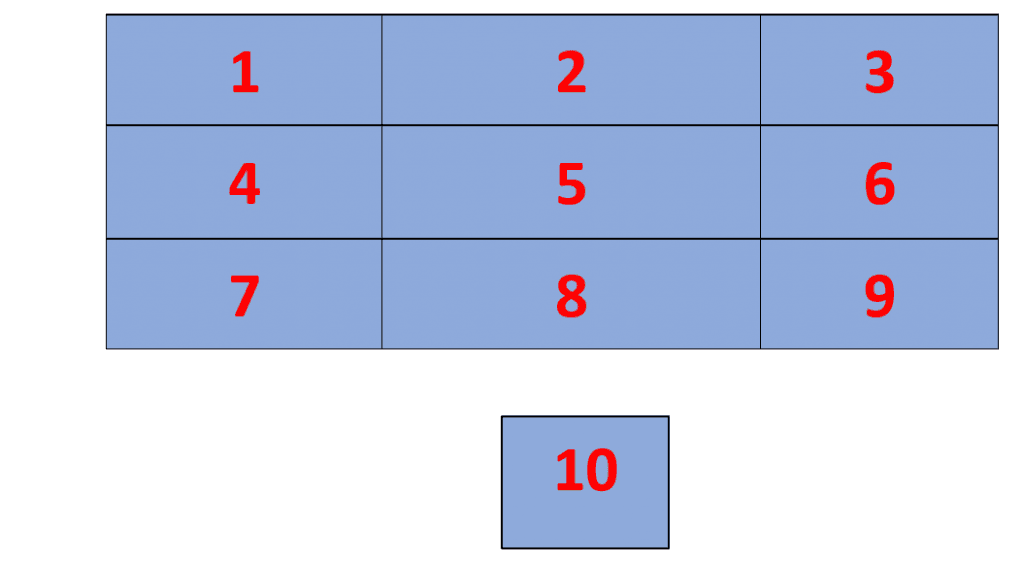
Digit Pattern of the 21 Times Table: The 21 times table follows a specific digit pattern that is easily learned. Draw a 3 x 3 grid and a separate 10th cell at the bottom. Now write natural numbers from 1 to 10 in ascending order starting from the top-left cell moving to the right and finishing at the bottom in the 10th cell as shown in the picture below.

21 times table pattern 1

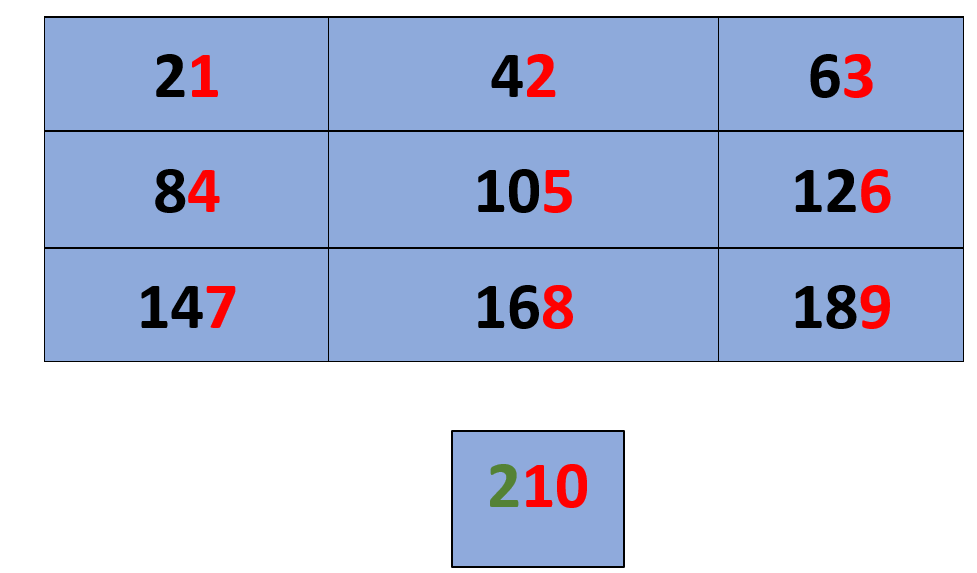
Once you have drawn the above table, write even numbers in ascending order, starting from the top-left corner and moving to the right, and ending at the ninth cell. In the tenth cell, just write the digit 2 before the number 10. The grid now contains the first 10 multiples of 21.

21 times table patterns 1

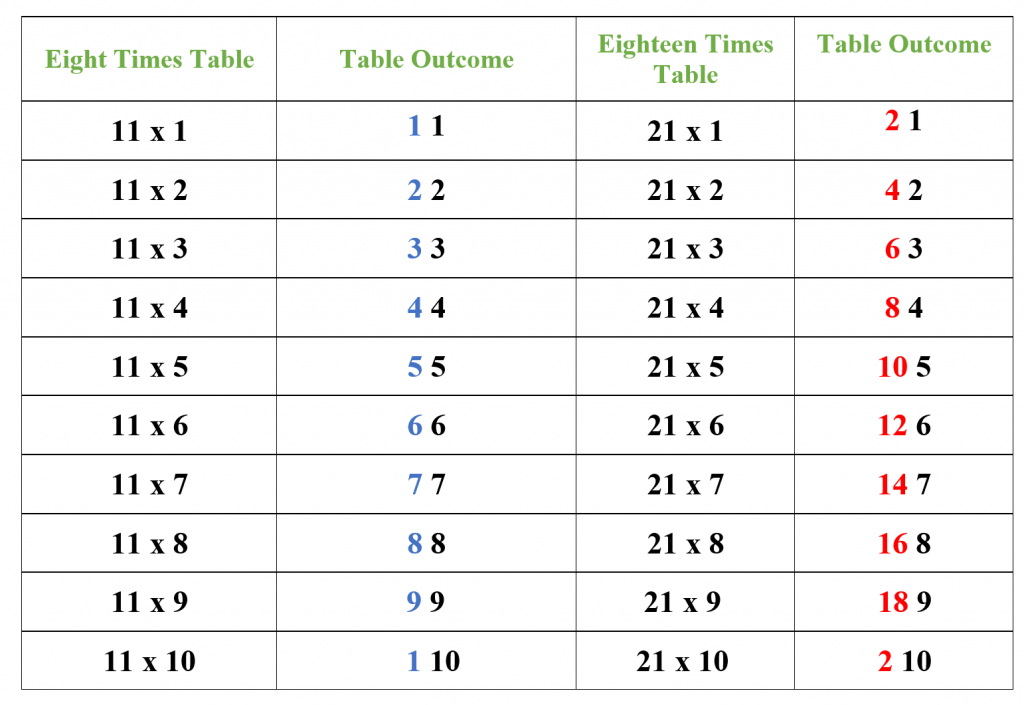
Using the 11 Times Table: The 11 times table can also be used in learning and understanding the 21 times table. This method is quite simple and effective, and it also helps you revise the 11 times table. All you have to do is write the 11 times table for the first 10 multiples and then double the value of the ten’s digits (shown in blue colors in the table below) while the rest of the digits remain the same. The doubled values are shown as red digits in the last column of the table.

21 times tables tips 1

Using the 20 Times Table: If you have memorized the 20 and the 2 times tables, then this method will help you learn and memorize the 22 times table in no time. The method involves adding the multiples of 20 to the multiples of 2; the results are the multiples of 22. For example, the fourth multiple of 20 is 80, and the fourth multiple of 2 is 8, and if we add 80 and 8, we get 88 that is the fourth multiple of the number 22. The detailed method is presented in the table below.

20 Times Table

Addition

Outcome

 $20\times 1 = {\color{green}20}$

${\color{green}20}+  {\color{red}1}$

$21$

$20\times 2 = {\color{green}40}$

${\color{green}40}+ {\color{red}2}$

$42$

$20\times 3 = {\color{green}60}$

${\color{green}60} + {\color{red}3}$

$63$

$20\times 4 = {\color{green}80}$

${\color{green}80}+ {\color{red}4}$

$84$

$20\times 5 = {\color{green}100}$

${\color{green}100} +{\color{red}5}$

$105$

$20\times 6 = {\color{green}120}$

${\color{green}120} +{\color{red}6}$

$126$

$20\times 7 = {\color{green}140}$

${\color{green}140} +{\color{red}7}$

$147$

$20\times 8 = {\color{green}160}$

${\color{green}160} + {\color{red}8}$

$168$

$20\times 9 = {\color{green}180}$

${\color{green}180} + {\color{red}9}$

$189$

$20\times 10 = {\color{green}200}$

${\color{green}200} + {\color{red}10}$

$210$

 

Table of 21 from 1 to 20:

A complete table of 21 from 1 to 20 can be written as:

Numerical Representation

Descriptive Representation

Product (Answer)

$21 \times 1$

Twenty-one times one

$21$

$21 \times 2$

Twenty-one times two

$42$

$21 \times 3$

Twenty-one times three

$63$

$21 \times 4$

Twenty-one times four

$84$

$21 \times 5$

Twenty-one times five

$105$

$21 \times 6$

Twenty-one times six

$126$

$21 \times 7$

Twenty-one times seven

$147$

$21 \times 8$

Twenty-one times eight

$168$

$21 \times 9$

Twenty-one times nine

$189$

$21 \times 10$

Twenty-one times ten

$210$

$21 \times 11$

 Twenty-one times eleven

$231$

$21 \times 12$

Twenty-one times twelve

$252$

$21 \times 13$

Twenty-one times thirteen

$273$

$21 \times 14$

Twenty-one times fourteen

$294$

$21 \times 15$

Twenty-one times fifteen

$315$

$21 \times 16$

Twenty-one times sixteen

$336$

$21 \times 17$

Twenty-one times seventeen

$357$

$21 \times 18$

Twenty-one times eighteen

$378$

$21 \times 19$

Twenty-one times nineteen

$399$

$21 \times 20$

Twenty-one times twenty

$420$

 

Example 1: Calculate 21 times 18 minus 570 plus 11 times 21

Solution:

21 times 18 minus 570 plus 11 times 21 can be written as:

$ = (21\times 18) – 570 + (11\times 21) $

$ = 378 – 570 + (11\times 21) $

$ = 378 – 570 + 231 $

$ = 378 + 231 – 570 $

$ = 609 – 570 $

$ = 39 $

Example 2: Ali is planning a birthday party, and he has bought 150 candies to distribute among his friends. If Ali distributes 5 candies among 21 of his friends, then calculate the remaining number of candies.

Solution:

Ali has a total of 150 candies.

We can calculate the number of distributed candies by using the 21 times table.

$21\times 5 = 105$ candies.

The number of remaining candies can be calculated by subtracting the distributed candies from the total number of candies.

Number of remaining candies = $150 – 105 = 45$ candies

Example 3: Calculate 3 times 3 times 2 times 21?

Solution:

3 times 3 times 2 times 21 can be written as:

$ = (3\times 3\times 2 \times 21) $

$ = (9\times 2\times 21) $

$ = (18 \times 21) $

$ = 378 $

Practice Questions:

1). Allan is participating in athletics and he follows a strict exercise regime and runs 21KM daily. Calculate the total distance covered by Allan.

  • If he follows his exercise regime for 7 days.
  • If he follows his exercise regime for 14 days.
  • If he follows his exercise regime for 19 days.

2). Subtract the sum of the first 5 even multiples of the number 21 from the first 5 odd multiples of the number 21.

3).  Calculate 21 times 15 times plus 100 minus 21 times 20?

4). Find the value of “Y” if “$ Y \times 21 = 21 \times 4 – 52 + 25 + 21 \times 7$.’’

5). From the given table, select the numbers which are multiples of 21.

1711831331135116180
22119021118110200267154
91191317167103189142
2121013415614010433138
2642652092152187147109
132169592970187292220
24813239341546999229
3151201683980100357231
4165455127312221463
44431984984132219119

Answer Key:

1). By using the 21 times table, we can calculate the distance covered by Ali.

  • If Ali follows the regime for 7 days, then the total distance is $21\times 7 = 147$.
  • The total distance covered by Ali in 14 days is $21\times 14 = 294$.
  • The total distance covered by Ali in 19 days is $21\times 19 = 399$.

2). We know the first 5 odd multiples of 21: 21, 63, 105, 147, and 189.

The first 5 even multiples of 21 are:  42, 84, 126, 168, and 210

Sum of the first 5 odd multiples of the number 21 is $= 21+ 63+ 105+ 147+ 189 = 525$.

Sum of the first 5 even multiples of the number 21 is $= 42 + 84 + 126 + 168 + 210 = 630$.

The difference between the sum of even and odd multiples is $= 630 – 525 = 105$.

3). 21 times 15 times plus 100 minus 21 times 20 can be written as:

$ = (21\times 15) + 100 – (21 \times 20) $

$ = 315 + 105 – (22\times 7) $

$ = 315 + 105 – 420$

$ = 420 – 420$

$ = 0 $

4). $ Y \times 21 = (21 \times 4) – 52 + 31 + (21 \times 7)$

$ Y \times 21 = 84 – 21 + 147 $.

$ Y \times 21 = 63 + 147 $.

$ Y \times 21 =  210 $.

We know that $21 \times 10 =210$, so

$ Y = 10 $.

5)

1711831331135116180
22119021118110200267154
91191317167103189142
2121013415614010433138
2642652092152187147109
132169592970187292220
24813239341546999229
3151201683980100357231
4165455127312221463
44431984984132219119