JUMP TO TOPIC
23 Times Table – Explanation & Examples
The 23 times table is the multiplication table of the number 23. As 23 is a prime number so like most prime numbers, learning and memorizing the 23 times table is a bit tricky. On the other hand, learning the 23 times table will help you solve complex multiplication and division-related problems.
23 times table is a table that contains the multiples of the number 23.
We will present some tips and patterns to help you learn and memorize the 23 times table in this topic.
You should refresh the following concepts to understand the material discussed on this topic.
- Basics of addition and multiplication
- 3 times table
- 20 times table
23 Multiplication Table
The table of 23 can be written as:
- $23 \times 1 = 23$
- $23 \times 2 = 46$
- $23 \times 3 = 69$
- $23 \times 4 =92$
- $23 \times 5 =115$
- $23 \times 6 =138$
- $23 \times 7 = 161$
- $23 \times 8 = 184$
- $23 \times 9 = 207$
- $23 \times 10 = 230$
Different tips for 23 Times Table:
The 23 times table is easy to understand and memorize if you know the tips and techniques. Let us look at some of these simple tips.
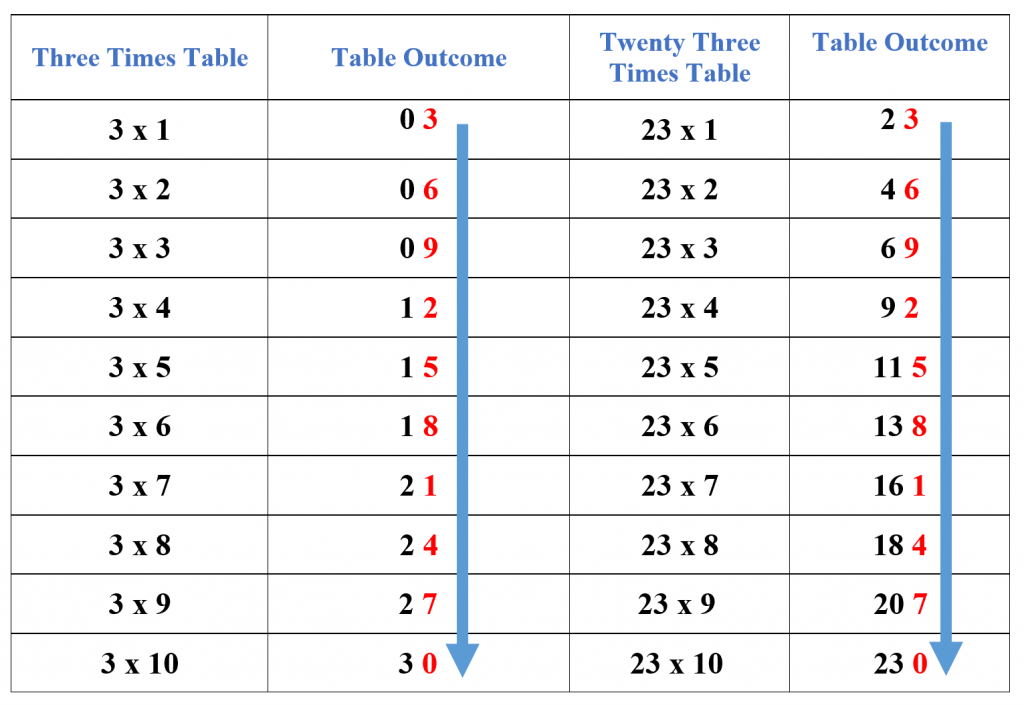
Digits Pattern of the 3 Times Table: As the name suggests, you have to remember the digits pattern of the 3 times table to help you memorize the 23 times table. The last digits of the first 10 multiples of the 3 times table are also the last digits of the first 10 multiples of the 23 times table. The pattern is illustrated in the table below.
Using the 20 and the 3 Times Table: If you have learned and memorized the 20 and the 3 times tables, this is one of the easiest methods to learn the 23 times tables, and it also helps in revising the previous tables. The method is simple; you add the outcomes of the 20 times table to the outcomes of the 3 times table, and the result is the 23 times table. For example, the sixth multiple of 20 is 120, and the sixth multiple of 3 is 18, and if we add 120 and 18, we get 138 which is the sixth multiple of 23. The detailed method is presented in the table below.
20 Times Table | 3 Times Table | Addition | Outcome |
| $20\times 1 = {\color{green}20}$ | $3 \times 1 = {\color{red}3}$ | ${\color{green}20}+ {\color{red}3}$ | $23$ |
$20\times 2 = {\color{green}40}$ | $3 \times 2 = {\color{red}6}$ | ${\color{green}40}+ {\color{red}6}$ | $46$ |
| $20\times 3 = {\color{green}60}$ | $3 \times 3 = {\color{red}9}$ | ${\color{green}60} + {\color{red}9}$ | $69$ |
$20\times 4 = {\color{green}80}$ | $3 \times 4 = {\color{red}12}$ | ${\color{green}80}+ {\color{red}12}$ | $92$ |
$20\times 5 = {\color{green}100}$ | $3 \times 5 = {\color{red}15}$ | ${\color{green}100} +{\color{red}15}$ | $115$ |
$20\times 6 = {\color{green}120}$ | $3 \times 6 = {\color{red}18}$ | ${\color{green}120} +{\color{red}18}$ | $138$ |
$20\times 7 = {\color{green}140}$ | $3 \times 7 = {\color{red}21}$ | ${\color{green}140} +{\color{red}21}$ | $161$ |
$20\times 8 = {\color{green}160}$ | $3 \times 8 = {\color{red}24}$ | ${\color{green}160} + {\color{red}24}$ | $184$ |
$20\times 9 = {\color{green}180}$ | $3 \times 9 ={\color{red}27}$ | ${\color{green}180} + {\color{red}27}$ | $207$ |
$20\times 10 = {\color{green}200}$ | $3 \times 10 = {\color{red}30}$ | ${\color{green}200} + {\color{red}30}$ | $230$ |
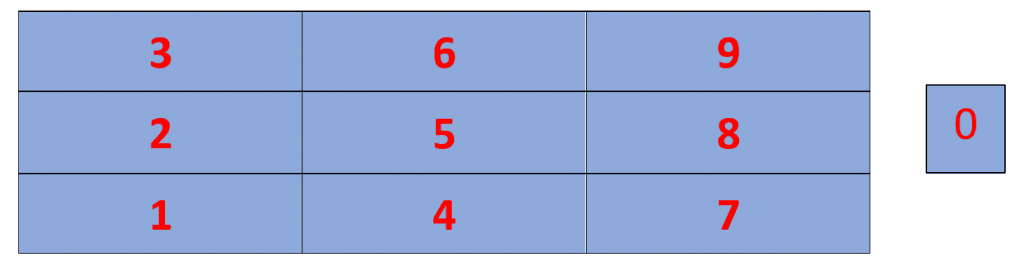
Digits Pattern: This method is simple and effective in learning and memorizing the 23 times table. First, draw a 3 x 3 table and write digits from 1 to 9 starting from the bottom left and moving upwards, and ending at the top right cell as shown by the red digits in the table below. The digit zero can be written separately.
Now follow a pattern of even, odd, and even numbers while skipping the fourth multiple in each case, as shown below. First, write the even digits 2, 4, and 6 from the top-right side to the top left and skip the number 8. In the second row, write the odd numbers 9, 11, and 13 and skip 15. In the last row, again write even numbers 16, 18, and 20 and skip 22. Finally, write 23 in the last remaining box. The resulting table contains the first 10 multiples of 23.
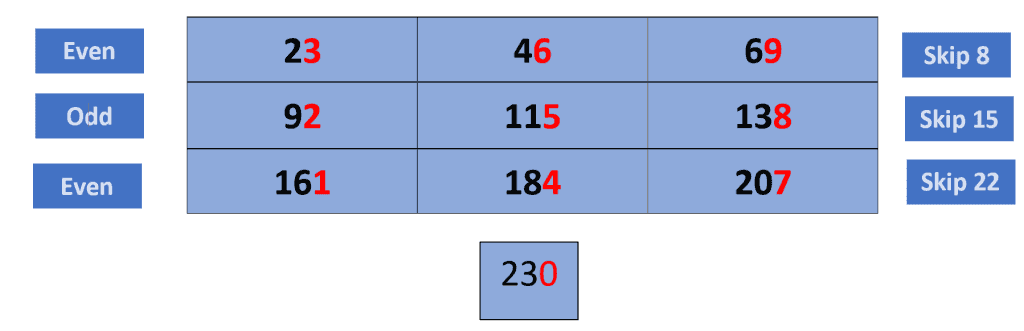
Table of 23 from 1 to 20:
A complete table of 23 from 1 to 20 can be written as:
Numerical Representation | Descriptive Representation | Product (Answer) |
$23 \times 1$ | Twenty-three times one | $23$ |
$23 \times 2$ | Twenty-three times two | $46$ |
$23 \times 3$ | Twenty-three times three | $69$ |
$23 \times 4$ | Twenty-three times four | $92$ |
$23 \times 5$ | Twenty-three times five | $115$ |
$23 \times 6$ | Twenty-three times six | $138$ |
$23 \times 7$ | Twenty-three times seven | $161$ |
$23 \times 8$ | Twenty-three times eight | $184$ |
| $23 \times 9$ | Twenty-three times nine | $207$ |
$23 \times 10$ | Twenty-three times ten | $230$ |
$23 \times 11$ | Twenty-three times eleven | $253$ |
$23 \times 12$ | Twenty-three times twelve | $276$ |
$23 \times 13$ | Twenty-three times thirteen | $299$ |
$23 \times 14$ | Twenty-three times fourteen | $322$ |
| $23 \times 15$ | Twenty-three times fifteen | $345$ |
$23 \times 16$ | Twenty-three times sixteen | $368$ |
$23 \times 17$ | Twenty-three times seventeen | $391$ |
$23 \times 18$ | Twenty-three times eighteen | $414$ |
$23 \times 19$ | Twenty-three times nineteen | $437$ |
$23 \times 20$ | Twenty-three times twenty | $460$ |
Example 1: Calculate 23 times 9 plus 110 minus 10 times 23.
Solution:
23 times 9 plus 210 minus 10 times 23 can be written as:
$ = (23\times 9) – 210 + (10 \times 23)$
$ = 207 – 210 + 230$
$ = 207 + 20 $
$ = 227 $
Example 2: Calculate 23 times 10 times 10 minus 2000.
Solution:
23 times 10 times 10 minus 2000 can be written as:
$ = 23\times10 \times 10 – 2000$
$ = 230\times 10 – 2000$
$ = 2300 – 2000$
$ = 300$
Example 3: Annie gets paid 23 dollars a day for working in a store. Using 23 times table calculate how much she will be paid,
- If Annie works for 10 days?
- If Annie works for 15 days?
Solution:
- Annie gets paid 23 dollars a day. By using the 23 times table, we can calculate the amount earned by Annie in 10 days as,
$23 \times 10 = 230$ dollars.
- The amount earned by Annie in 15 days is
$23 \times 15 = 355$ dollars.
Example 4: Verify whether the seventh multiple of the number 23 is 161 or not?
Solution:
We know the first 10 multiples of 23 are 23, 46, 69, 92, 115, 138, 161, 184, 207, and 230.
So, the seventh multiple of the number 23 is 161.
Practice Questions:
- Mendy went to a shop to buy some clothes for an upcoming event. Mendy bought seven shirts and eight pairs of pants. The cost of each shirt and each pair of pants was 23 dollars. Calculate the total amount Mendy spent on the clothes.
- Find the value of “Y” if “$ Y\times 23 = 23\times 14 – 675 + 23\times 20 + 100$.’’
- Danial is arranging a farewell party for six of his friends who are leaving the town. Danial wants to give each friend a chocolate box having 23 chocolates in it. Help Danial calculate the total number of chocolates required so that each box has 23 chocolates in it.
- From the given table, select the numbers which are multiples of 23
| 24 | 38 | 18 | 23 | 51 | 269 | 184 |
| 41 | 69 | 74 | 96 | 19 | 115 | 111 |
| 48 | 72 | 98 | 94 | 99 | 104 | 211 |
| 120 | 131 | 49 | 121 | 118 | 113 | 47 |
| 138 | 260 | 216 | 52 | 114 | 112 | 92 |
| 109 | 414 | 413 | 79 | 460 | 89 | 134 |
| 191 | 73 | 437 | 179 | 65 | 215 | 195 |
| 99 | 156 | 154 | 299 | 161 | 208 | 138 |
| 221 | 84 | 77 | 345 | 227 | 96 | 266 |
| 64 | 68 | 155 | 159 | 196 | 230 | 170 |
| 119 | 121 | 57 | 51 | 190 | 345 | 171 |
Answer Key:
1) The cost of one shirt = 23 dollars and cost of one pair of pants = 23 dollars
Mendy bought 7 shirts and 8 pairs of pants. We can use the 23 times table to calculate the total amount.
Cost of 7 shirts $= 23\times 7 = 161$
Cost of 8 pairs of pants $= 23\times 8 = 184$
Total amount $= 161 + 184 = 345$ dollars.
2) $ Y \times 23 = (23\times 14) – 675 + (23\times 20) + 100$.
$ Y \times 23 = 322 – 675 + 460 + 100 $.
$ Y \times 23 = 322 – 675 + 560 $.
$ Y \times 23 = 322 – 115 $.
$Y \times 23 = 207 $
We know that $23\times 9 =207$, so
$ Y = 9 $.
3) Danial wants to give the chocolate box to six of his friends and each box should contain 23 chocolates. So, the total number of required chocolates can be calculated using the 23 times table
$= 23\times 6 = 138$ chocolates
4)
| 24 | 38 | 18 | 23 | 51 | 269 | 184 |
| 41 | 69 | 74 | 96 | 19 | 115 | 111 |
| 48 | 72 | 98 | 94 | 99 | 104 | 211 |
| 120 | 131 | 49 | 121 | 118 | 113 | 47 |
| 138 | 260 | 216 | 52 | 114 | 112 | 92 |
| 109 | 414 | 413 | 79 | 460 | 89 | 134 |
| 191 | 73 | 437 | 179 | 65 | 215 | 195 |
| 99 | 156 | 154 | 299 | 161 | 208 | 138 |
| 221 | 84 | 77 | 345 | 227 | 96 | 266 |
| 64 | 68 | 155 | 159 | 196 | 230 | 170 |
| 119 | 121 | 57 | 51 | 190 | 345 | 171 |