3 4 5 Right Triangles – Explanation & Examples

Right triangles are very useful in our daily life. The simpler the dimensions of a right triangle, the simpler is its use.

The ability to recognize special right triangles is the shortcut to solving problems involving right triangles. Instead of using the Pythagorean theorem, you can use special right triangle ratios to calculate the missing lengths.

They may have different dimensions, but the most common of them is the 3-4-5 right triangle. This article will discuss what a 3-4-5 right triangle is and how to solve problems involving the 3-4-5 right triangle.

A triangle is a two-dimensional polygon with three corners, three vertices, and three angles joined together, forming a closed diagram in geometry. There are different types of triangles depending on the side lengths and magnitude of their interior angles. For more details on triangles, you can go through the previous articles.

What is a 3-4-5 Right Triangle?

A 3-4-5 right triangle is a triangle whose side lengths are in the ratio of 3:4:5. In other words, a 3-4-5 triangle has the ratio of the sides in whole numbers called Pythagorean Triples.

This ratio can be given as:

Side 1: Side 2: Hypotenuse = 3n: 4n: 5n = 3: 4: 5

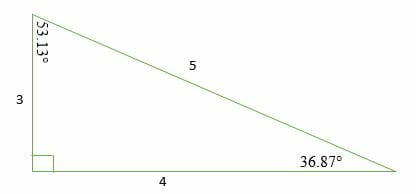
We can prove this by using the Pythagorean Theorem as follows:

⇒ a² + b² = c²

⇒ 3² + 4² = 5²

⇒ 9 + 16 = 25

25 = 25

A 3-4-5 right triangle has the three internal angles as 36.87 °, 53.13 °, and 90 °. Therefore, a 3 4 5 right triangle can be classified as a scalene triangle because all its three sides lengths and internal angles are different

Remember that a 3-4-5 triangle does not mean that the ratios are exactly 3: 4: 5; it can be any common factor of these numbers. For example, a 3-4-5 triangle can also take the following forms:

• 6-8-10
• 9-12-15
• 12-16-20
• 15-20-25

How to Solve a 3-4-5 Triangle

Solving a 3-4-5 right triangle is the process of finding the missing side lengths of the triangle. The ratio of 3: 4: 5 allows us to quickly calculate various lengths in geometric problems without resorting to methods such as tables or the Pythagoras theorem.

Example 1

Find the length of one side of a right triangle in which hypotenuse and the other side measures 30 cm and 24 cm, respectively.

Solution

Test the ratio to see if it fits the 3n: 4n: 5n

?: 24: 30 = ?: 4(6): 5(6)

This must be a 3-4-5 right triangle, so we have;

n = 6

Hence the length of the other side is;

3n = 3(6) = 18 cm

Example 2

The longest edge and bottom edge of a sailboat’s triangular sail are 15 yards and 12 yards, respectively. How tall is the sail?

Solution

Test the ratio

⇒ ?: 12: 15 = ? : 4(3) : 5(3)

Therefore, the value of n = 3

Substitute.

⇒ 3n = 3(3) = 9

Hence, the height of the sail is 9 yards.

Example 3

Identify the 3-4-5 right triangle from the following list of triangles.

1. Triangle A ⇒ 8, 8, 25
2. Triangle B ⇒ 9, 12, 15
3. Triangle C ⇒ 23, 27, 31
4. Triangle D ⇒ 12, 16, 20
5. Triangle E ⇒ 6, 8, 10

Solution

Test the ratio of each triangle.

A ⇒ 8: 8: 25

B ⇒ 9: 12: 15 (divide each term by 3)

= 3: 4: 5

C ⇒23: 27: 31

D ⇒ 12: 16: 20 (divide each term by 4)

= 3: 4: 5

E ⇒6: 8: 10 (divide through by 2)

= 3: 4: 5

Therefore, triangles B, D, and E are 3-4-5 right triangles.

Example 4

Find the value of x in the figure shown below. Assume the triangle is a 3-4-5 right triangle.

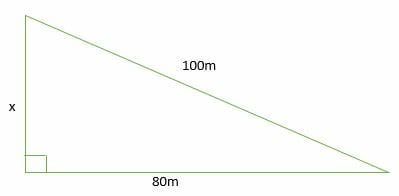
Solution

Look for the factor “n” in a 3-4-5 right triangle.

?: 80: 100 = ?: 4(20): 5(20)

Hence, n = 20

Substitute in 3n: 4n: 5n.

3n = 3(20) = 60

Therefore, x = 60 m

Example 5

Calculate the length of the diagonal of a right triangle with side lengths of 6 inches and 8 inches.

Solution

Check the ratio if it fits the 3n: 4n: 5n ratio.

6: 8: ? = 3(2): 4(2):?

n =2

Substitute n= 2 in 5n.

5n = 5(2) = 10.

Therefore, the length of the diagonal is 10 inches.