• Home
  • >
  • 3 Times Table – Explanation & Examples

3 Times Table – Explanation & Examples

3 Times TableOnce we are comfortable with the 2 times table, it is then time to move to the next table, the 3 times table.

3 times table is a table that contains multiples of the number 3.

Learning the table of 3 might not be as simple as the 2 times table. However, we will discuss some interesting tips and tricks to learn and understand the 3 times table quickly and easily.

It is advisable to refresh the following concepts to understand this topic better.

  1. Basics of addition and multiplication
  2. 2 times table 

3 Times Table

The table of 3 can be written as:

  • $3\times1 = 3$
  • $3\times 2 = 6$
  • $3\times 3 = 9$
  • $3\times 4 =12$
  • $3\times 5 =15$
  • $3\times 6 =18$
  • $3\times 7 = 21$
  • $3\times 8 = 24$
  • $3\times 9 = 21$
  • $3\times 10= 30$

Different Tips for Learning the 3 Times Table

If we know addition and the 2 times table, it is easy to learn the 3 times table. Let’s take a look at some simple tips which can help you memorize the 3 times table.

  • Digit placement: This is one of the easiest methods to learn the 3 times table up to the 10th multiple. It involves simple digits placement in a table. First, draw a table having 3 columns and 3 rows. Now write 0, 1, and 2 from top to bottom in all the three columns. 
${{\color{green}0}}$${{\color{green}0}}$${{\color{green}0}}$
${{\color{green}1}}$${{\color{green}1}}$${{\color{green}1}}$
${{\color{green}2}}$${{\color{green}2}}$${{\color{green}2}}$

Then write the natural numbers from 1 to 9 in ascending order from the bottom left box and carry on writing towards the top right one.

${{\color{green}0}{\color{red}3}}$${{\color{green}0}{\color{red}6}}$${{\color{green}0}{\color{red}9}}$
${{\color{green}1}{\color{red}2}}$${{\color{green}1}{\color{red}5}}$${{\color{green}1}{\color{red}8}}$
${{\color{green}2}{\color{red}1}}$${{\color{green}2}{\color{red}4}}$${{\color{green}2}{\color{red}7}}$

The natural numbers are written in red, and the resultant table now represents 3 times tables up to the 9th multiple of 3, which is 27. Using this table, we can easily learn the table up to the 9th multiple; while, the 10th multiple of 3 is 30, which can be memorized separately.

  • Using the 2 times table: Students who have learned and understood the 2 times table could use it to create the 3 times table using the method described below.

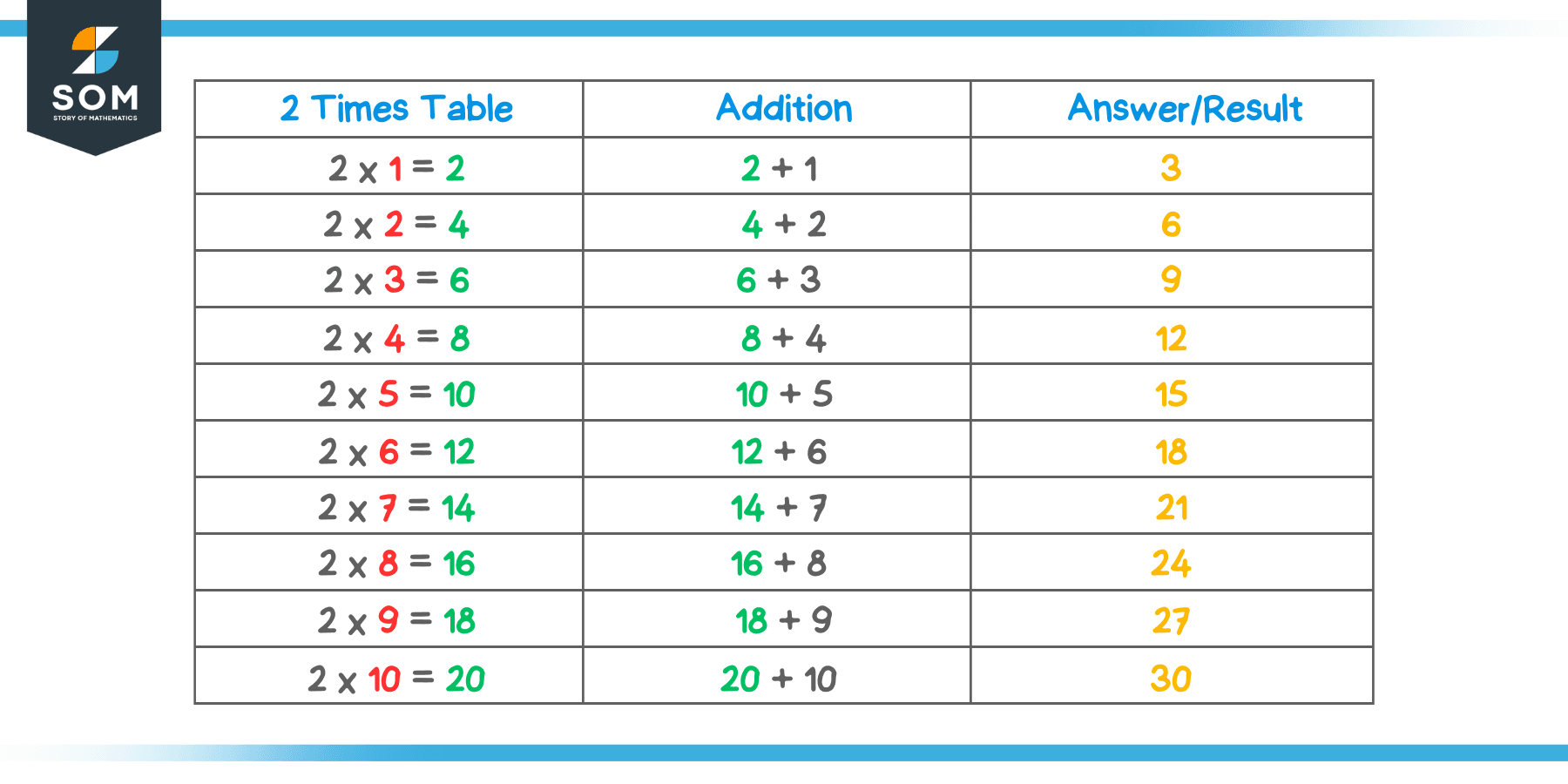
3 Times Table using 2 Times Table

The first column contains the 2 times table, and the answers of the 2 times table are shown in green color.  In the second column, we add a natural number (shown in red) to the answer of the 2 times table. Note that it is the same number that is being multiplied by 2 in the 2 times table.  If we add the green digits to the red ones in each row from top to bottom, we get the answers for the 3 times table. For example, in the first row adding $2+1= 3$, which is equal to $3\times 1 =3$. Similarly, in the second row, $4+2 =6$, which is equal to $3\times2 = 6$.

  • Using 1 times table and multiples of 2: This method involves using 1 times table and multiples of 2 to produce the results of the 3 times table.

3 Times Table using 1 Times Table

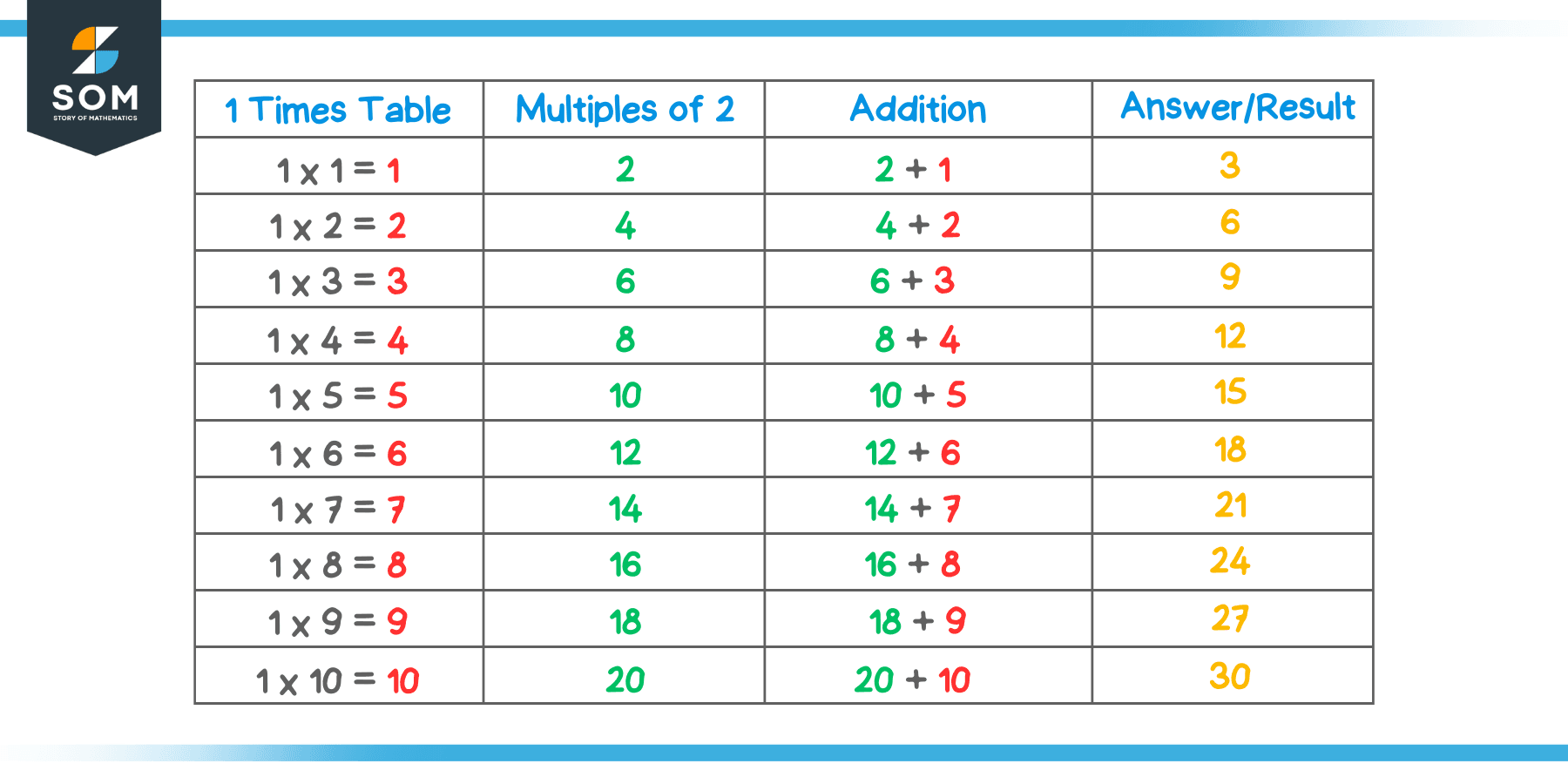
The first column is the 1 times table, while the second column shows the multiples of two. If we add each row of the first two columns, the answer represents the 3 times table. For example, $1\times 3 = 3$, while the third multiple of 2 is 6, so $3+6= 9$, which is equal to the third row of the 3 times table, i.e., $3\times 3 = 9$. Similarly, $1\times 10 = 10$, while the 10th multiple of 2 is 20. Adding these two, we get $10+20 = 30$, which is equal to the 10th row of the 3 times table i.e., $3\times 10 = 30$.

Addition: If you are still having difficulty in memorizing the 2 times and 3 times table, you can use the simple addition method to understand the basics of the 3 times table. Let us take an example: Sarah has no oranges at the start, and then she is given 3 oranges, so $0+3 =3$. After that she is given 3 more oranges and now Sarah has $3+3 = 6$ oranges. Again she is given 3 more oranges, so the total number of oranges is 9.

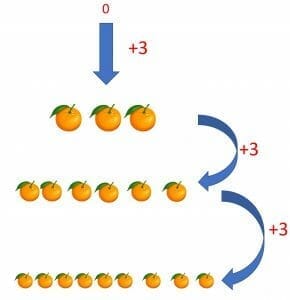
Addition method to understand 3 times table

If we keep on adding 3s, we will form a 3 times table.
$0+3=3$
$3+3=6$
$6+3=9$
$9+3=12$
$12+3=15$ and so on

  • Recitation: Students who are having difficulty in addition or multiplication can recite the three times loudly and repeatedly. Once they have memorized it, it will be easier to teach them through the addition or multiplication method. Read this out loud.

    1 times 3 is 3
    2 times 3 is 6
    3 times 3 is 9
    4 times 3 is 12
    5 times 3 is 15
    6 times 3 is 18
    7 times 3 is 21
    8 times 3 is 24
    9 times 3 is 27
    10 times 3 is 30

Table of 3 From 1 to 15:

We can write a complete table of 3 from 1 to 15 as:

Numerical Representation

Descriptive Representation

Product (Answer)

$3\times1$

Three times one

$3$

$3\times 2$

Three times two

$6$

$3\times 3$

Three times three

$9$

$3\times 4$

Three times four

$12$

$3\times 5$

Three times five

$15$

$3\times 6$

Three times six

$18$

$3\times 7$

Three times seven

$21$

$3\times 8$

Three times eight

$24$

$3\times 9$

Three times nine

$27$

$3\times 10$

Three times ten

$30$

$3\times 11$

Three times eleven

$33$

$3\times 12$

Three times twelve

$36$

$3\times 13$

Three times thirteen

$39$

$3\times 14$

Three times fourteen

$42$

$3\times 15$

Three times fifteen

$45$

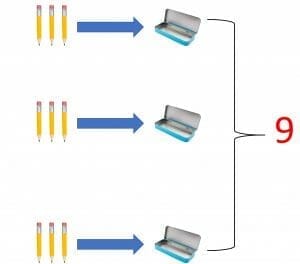
Example 1: Claire has nine pencils and three pencil boxes. She wants to put an equal number of pencils in each pencil box. How many pencils should each box contain?

Solution:

Claire has nine pencils

pencils example 3 times table

If Claire uses the 3 times table, she can easily calculate the number of pencils she should put in each pencil box so that all the boxes contain an equal number of pencils.

  • $3\times1 = 3$
  • $3\times 2 = 6$
  • $3\times 3 = 9$

Claire has 3 pencil boxes, so if Claire puts 3 pencils in each pencil box, she will have an equal number of pencils in all the boxes.

3 times table easy example 1

Example 2: Using the 3 times table, calculate 3 plus 3 times 6

Solution:

3 plus 3 times 6 can be written as: $ 3+3\times 6 $.

Applying the First Divide then Multiply then Add then Subtract (DMAS) rule, we will multiply first and then we will do addition.

$3\times 6 = 18$. So  $3+18 = 21$ is answer.

Example 3: Using 3 times table, calculate 6 plus 3 times 9 minus 4.

Solution:

6 plus 3 times 9 minus 4 can be written as: $ 6+3\times9- 4 $

$ = 6 + (3\times9) – 4 $

$ = 6 + 27 – 4 $

$ = 6+ 23 $

$ = 29 $

Example 4: Leo works in a shop, and he is paid 10 dollars for a 3-hour shift. Calculate the total number of shifts if:

  1. Leo works for 6 hours
  2. Leo works for 9 hours
  3. Leo works for 15 hours

Solution: 
1. If Leo works for 6 hours, then the total number of shifts is 2. It can be calculated using 3 times table as $3 \times 2 = 6$. 

2. If Leo works for 9 hours, then the total number of shifts is 3. It can be calculated using 3 times table as $3 \times 3 = 9$. 

3. If Leo works for 15 hours, we can calculate the total number of shifts using a 3 times table as $3\times 5 = 154$. So, Leo does 5 shifts.

Practice Questions:

  1. Eve is given 3 dollars in pocket money every day. Eve saves her pocket money. Calculate the total amount of money she has saved at the end of the week.
  2. Using 3 times table, calculate  3 times 3 minus 2 times 3.
  3. From the given table, select the numbers which are multiples of 3. 
27111312
151932210
0125109
161819820
3156927
4414152930
3332313435

Answer Key:

  1. A week has 7 days. So, the total amount of pocket money would be $3\times 7 = 21 $ dollars
  2. 3 times 3 minus 2 times 3 can be written as:

    $ 3\times3-2\times3$

    $ = (3\times3) – (2\times3) $

    $ = 9 – 6$

    $ = 3$

      3. 

27111312
151932210
01251024
161819820
3156927
4414212930
3332313435