- Home
- >
- 5 Times Table – Explanation & Examples
JUMP TO TOPIC
5 Times Table – Explanation & Examples
 5 times table is one of the most commonly used tables in solving mathematical problems related to fractions, multiplications, divisions, least common multiples, greatest common divisors, etc. Also, It is one of the easiest tables to learn and understand.
5 times table is one of the most commonly used tables in solving mathematical problems related to fractions, multiplications, divisions, least common multiples, greatest common divisors, etc. Also, It is one of the easiest tables to learn and understand.
5 times table is a table that contains multiples of the number 5.
Learning and understanding the 5 times table is quite easy as it follows a simple pattern. This topic will provide your with useful tips to easily learn and understand the 5 times table.
You should refresh the following concepts to understand the material discussed in this topic.
- Basics of addition and multiplication
- 1 times Table
- 2 times table
- 4 times table
5 Multiplication Table
We can write the table of 5 as:
- $5 \times 1 = 5$
- $5 \times 2 = 10$
- $5 \times 3 = 15$
- $5 \times 4 =20$
- $5 \times 5 =25$
- $5 \times 6 =30$
- $5 \times 7 = 35$
- $5 \times 8 = 40$
- $5 \times 9 = 45$
- $5 \times 10 = 50$
Different Tips for 5 Times Table
Let us look at some simple tips which can help you memorize the 5 times table.
- Using the 4 times table: This is one of the simplest ways for students to learn the 5 times table. This method will help revise the 4 times table and understand the 5 times table at the same time.
4 Times Table | Addition | (Answer) | 5 Times Table |
$4 \times 1 = 4$ | $4 + 1$ | $5$ | $ 5 \times 1 = 5$ |
| $4 \times 2 = 8$ | $8 + 2$ | $10$ | $5 \times 2 = 10$ |
$4 \times 3 = 12$ | $12 + 3$ | $15$ | $5 \times 3 = 15$ |
| $4 \times 4 = 16$ | $16 + 4$ | $20$ | $5 \times 4 =20$ |
$4 \times 5 = 20$ | $20 + 5$ | $25$ | $5 \times 5 =25$ |
| $4 \times 6 = 24$ | $24 + 6$ | $30$ | $5 \times 6 =30$ |
$4 \times 7 = 28$ | $28 + 7$ | $35$ | $5 \times 7 = 35$ |
| $4 \times 8 = 32$ | $32 + 8$ | $40$ | $5 \times 8 = 40$ |
$4 \times 9 = 36$ | $36 + 9$ | $45$ | $5 \times 9 = 45$ |
| $4 \times 10 = 40$ | $40 + 10$ | $50$ | $5 \times 10 = 50$ |
As we can see, in the first row, the outcome of $4\times 1$ is $4$, and if we add to it the natural number being multiplied by 4 ($1$ in this case), the answer will be the first multiple of 5.
Similarly, in the second row, the outcome of $4\times 2$ is $8$, and if we add to it the natural number being multiplied by 4 ($2$ in this example), the answer will be 10, which is the second multiple of 5. If we continue doing this, we get the 5 times table.
- Digits Pattern: The 5 times table follows a specific pattern. All the multiples of 5 contain either the number 5 or 0 at the end. The pattern for the first 10 multiples of 5 is given below.

To learn this method, draw a table having 4 columns and 10 rows. In the first column, write numbers from $0$ to $5$, where each number is written twice, apart from $0$ and $5$, written only once. In the second column, write the digits 5 and 0 alternately (starting with 5) from top to bottom. In the third column, combine the digits of the first two columns.
For example, the third row of the first column contains the digit $1$, and the third row of the second column contains the digit $5$; if we combine these two, we get the third multiple of 5, which is 15. If we continue with the row-wise combination of the first two columns, the resultant third column will contain multiples of $5$ in ascending order.
The fourth column is the 5 times table with the same outcomes as the third column.
First Digit | Digit Pattern of $5$ and $0$ | Combination | 5 Times Table |
0 | 5 | 05 | 5 x 1 = 5 |
| 1 | 0 | 10 | 5 x 2 = 10 |
1 | 5 | 15 | 5 x 3 = 15 |
| 2 | 0 | 20 | 5 x 4 =20 |
2 | 5 | 25 | 5 x 5 =25 |
| 3 | 0 | 30 | 5 x 6 =30 |
3 | 5 | 35 | 5 x 7 = 35 |
| 4 | 0 | 40 | 5 x 8 = 40 |
4 | 5 | 45 | 5 x 9 = 45 |
| 5 | 0 | 50 | 5 x 10 = 50 |
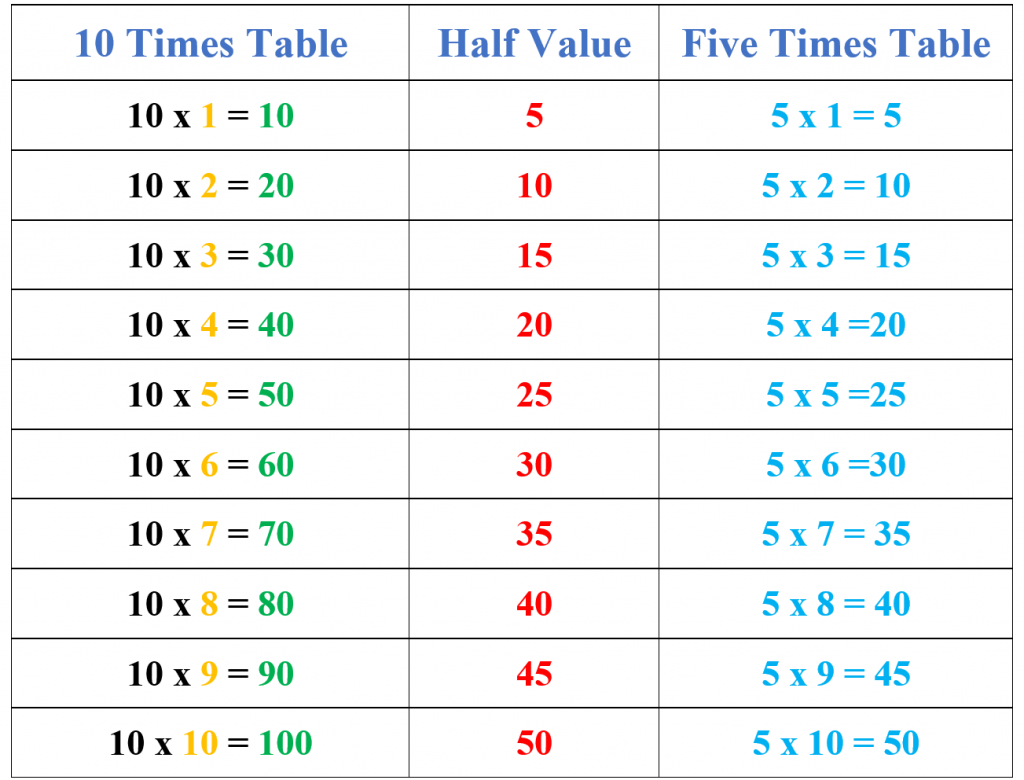
- Using the 10 times table: This method is beneficial as students learn the 10 times table in advance while also learning the easiest technique to master the 5 times table. In this method, we first write the 10 times table. If we divide each multiple of 10 by 2 (in other words, get half of each multiple), it will give us the multiples of 5.
- Recitation: Reciting the table loudly and repeatedly can benefit students who are having difficulty in addition or multiplication. Try reading this out loud:5 times 1 is 5
5 times 2 is 10
5 times 3 is 15
5 times 4 is 20
5 times 5 is 25
5 times 6 is 30
5 times 7 is 35
5 times 8 is 40
5 times 9 is 45
5 times 10 is 50
Table of 5 From 1 to 20:
A complete table of 5 from 1 to 20 can be written as:
Numerical Representation | Descriptive Representation | Product (Answer) |
$5 \times 1$ | Five times one | $5$ |
| $5 \times 2$ | Five times two | $10$ |
$5 \times 3$ | Five times three | $15$ |
| $5 \times 4$ | Five times four | $20$ |
$5 \times 5$ | Five times five | $25$ |
| $5 \times 6$ | Five times six | $30$ |
$5 \times 7$ | Five times seven | $35$ |
| $5 \times 8$ | Five times eight | $40$ |
$5 \times 9$ | Five times nine | $45$ |
| $5 \times 10$ | Five times ten | $50$ |
$5 \times 11$ | Five times eleven | $55$ |
| $5 \times 12$ | Five times twelve | $60$ |
$5 \times 13$ | Five times thirteen | $65$ |
| $5 \times 14$ | Five times fourteen | $70$ |
$5 \times 15$ | Five times fifteen | $75$ |
| $5 \times 16$ | Five times sixteen | $80$ |
$5 \times 17$ | Five times seventeen | $85$ |
| $5 \times 18$ | Five times eighteen | $90$ |
$5 \times 19$ | Five times nineteen | $95$ |
| $5 \times 20$ | Five times twenty | $100$ |
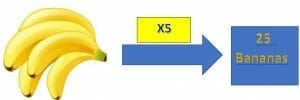
Example 1: Harrison has 5 bananas. If Harrison wants to convert 5 bananas to 25 bananas, which number should he multiply the 5 bananas with?
Solution:
Harrison knows the 5 times table.
$5\times 5 = 25$
So if Harrison multiplies $5$ with $5$, he will get 25 bananas.
Example 2: Calculate 5 times 2 times 5?
Solution:
5 times 2 times 5 can be written as:
$ 5\times 2 \times 5$
$ = 10\times 5$
$ = 50$
Example 3: Calculate 5 times 2 plus 7 times 5?
Solution:
5 times 2 plus 7 times 5 can be written as:
$ = (5\times 2) + (7\times 5)$
$ = 10 + 35$
$ = 45$
Example 4: Morgan has a pencil box that contains five pencils. Calculate the total number of pencils using 5 times table if
- Morgan has 31 pencil boxes
- Morgan has 43 pencil boxes
- Morgan has 50 pencil boxes
Solution:
- If Morgan has 31 pencil boxes, then the total number of pencils can be calculated as: $5 \times 31 = 155$ pencils.
- If Morgan has 43 pencil boxes, then the total number of pencils can be calculated as: $5 \times 43 = 215$ pencils.
- If Morgan has 50 pencil boxes, then the total number of pencils can be calculated as: $5 \times 50 = 250 $ pencils.
Example 5: Sarah loves to write stories. She can write a single story in five days. How many days will it take her to write six stories?
Solution:
Using the 5 times table, we know that $5 \times 6 =30$. So it will take Sarah 30 days to write 6 stories.
Practice Questions:
- Allan and his four friends have five pencils each. Calculate the total number of pencils.
- What is the product of 5 times 2 times 5?
- What is the 7th multiple of 5?
- From the given table, select the numbers which are multiples of 5.
| 12 | 27 | 36 | 40 | 5 |
| 25 | 19 | 20 | 18 | 10 |
| 9 | 11 | 13 | 17 | 15 |
| 15 | 23 | 14 | 16 | 30 |
| 31 | 29 | 10 | 25 | 21 |
| 32 | 14 | 55 | 29 | 50 |
| 41 | 32 | 39 | 34 | 35 |
| 37 | 100 | 26 | 39 | 80 |
| 41 | 65 | 43 | 51 | 45 |
| 44 | 43 | 59 | 49 | 60 |
Answer Key
1) There are a total of 5 persons, and each has 5 pencils. So by using 5 times table
$= 5\times 5 =25$ pencils
2) 5 times 2 times 5 can be written as:
$ = 5\times 2 \times 5$
$ = 10 \times 5$
$ = 50$
3) Multiples of 5 can be written as: 5, 10, 15, 20, 25, 30, 35, 40, 45, 50
So, the 7th multiple is 35.
4)
| 12 | 27 | 36 | 40 | 5 |
| 25 | 19 | 20 | 18 | 10 |
| 9 | 11 | 13 | 17 | 75 |
| 15 | 23 | 14 | 16 | 30 |
| 31 | 29 | 10 | 25 | 21 |
| 32 | 14 | 55 | 29 | 50 |
| 41 | 32 | 39 | 34 | 35 |
| 37 | 100 | 26 | 39 | 80 |
| 41 | 65 | 43 | 51 | 45 |
| 44 | 43 | 59 | 49 | 60 |
