JUMP TO TOPIC
7 times table – Explanation & Examples
The 7 times table is a very important multiplication table. Seven is a prime number, and it has a great significance in our lives; for example, the number of days in a week and the total number of continents in the world are 7. Seven is also considered a lucky number in some cultures.
The 7 times table is a table that contains multiples of the number 7.
Learning and understanding the 7 times table is essential for solving multiplication, division, and factorization-related mathematical problems. It also helps in problems related to calculating the total number of weeks in a month or a year, etc.
Unlike previous tables, the 7 times table is somewhat difficult as it does not follow any simple patterns. This topic will present some tips that will help students learn and memorize the 7 times table.
You should refresh the following concepts to understand this topic better.
- Basics of addition and multiplication.
- Five times table
- Six times table
7 multiplication table
We can write the table of 7 as:
- $7\times1 = 7$
- $7 \times 2 = 14$
- $7 \times 3 = 21$
- $7 \times 4 =28$
- $7 \times 5 =35$
- $7 \times 6 =42$
- $7 \times 7 = 49$
- $7 \times 8 = 56$
- $7 \times 9 = 63$
- $7 \times 10 = 70$
Different tips for 7 times table:
As we said earlier, the 7 times table is considered a difficult table to learn and memorize. So, whats makes it tricky and difficult? The answer is that 7 is a prime number, and it is only divisible by itself and 1.
Furthermore, the addition method (adding 7 to 0, then 7 to 7, 7 to 14, and so on.) generates numbers that follow no simple and identifiable pattern. Still, some tips and tricks are useful for learning the 7 times table, as discussed below.
Using the 6 Times table: If the students have memorized the six-time table, this is one of the easiest methods to learn the 7 times table. In this method, if we add natural numbers in increasing order to the multiples of 6, we get the 7 times table.
The first multiple of 6 is added with the first natural number, i.e., 1. The second multiple of 6 is added with the second natural number, i.e., 7 and so on. This method is presented in the table below.
Six Times Table | Addition | (Answer) | Six Times Table |
$6\times {\color{#cccc00}1} = {\color{green}6}$ | ${\color{green}6} +{\color{#cccc00} 1}$ | ${\color{red}7}$ | $ 7 \times 1 = 7$ |
| $6\times {\color{#cccc00}2} = {\color{green}12}$ | ${\color{green}12} +{\color{#cccc00} 2}$ | ${\color{red}14}$ | $7 \times 2 = 14$ |
$6\times {\color{#cccc00}3} = {\color{green}18}$ | ${\color{green}18} +{\color{#cccc00} 3}$ | ${\color{red}21}$ | $7 \times 3 = 21$ |
| $6\times {\color{#cccc00}4} = {\color{green}24}$ | ${\color{green}24} +{\color{#cccc00} 4}$ | ${\color{red}28}$ | $7 \times 4 =28$ |
$6\times {\color{#cccc00}5} = {\color{green}30}$ | ${\color{green}30} +{\color{#cccc00} 5}$ | ${\color{red}35}$ | $7 \times 5 =35$ |
| $6\times {\color{#cccc00}6} = {\color{green}36}$ | ${\color{green}36} +{\color{#cccc00} 6}$ | ${\color{red}42}$ | $7 \times 6 =42$ |
$6\times {\color{#cccc00}7} = {\color{green}42}$ | ${\color{green}42} +{\color{#cccc00} 7}$ | ${\color{red}49}$ | $7 \times 7 = 49$ |
| $6\times {\color{#cccc00}8} = {\color{green}48}$ | ${\color{green}48} +{\color{#cccc00} 8}$ | ${\color{red}56}$ | $7 \times 8 = 56$ |
$6\times {\color{#cccc00}9} = {\color{green}54}$ | ${\color{green}54} +{\color{#cccc00} 9}$ | ${\color{red}63}$ | $7 \times 9 = 63$ |
| $6\times {\color{#cccc00}10} = {\color{green}60}$ | ${\color{green}60} +{\color{#cccc00} 10}$ | ${\color{red}70}$ | $7 \times 10 = 70$ |
- Using the 5 times table: This method is quite similar to the above method. 5 times table is easier as compared to 6 times table, so those students who haven’t learned and memorized the 6 times table can use this method. In this method, the multiples of 5 are added with even numbers in ascending order from top to bottom.
For example, the first multiple of 5 will be added with the first even number, i.e., 2. The second multiple of 5, i.e.,10, will be added with the second even number, i.e., 4, and so on. The resulting table is the 7 times table.
Five Times Table | Addition of Even Numbers | (Answer) | Six Times Table |
$5\times 1 = {\color{green}5}$ | ${\color{green}5} +{ \color{#cccc00}2}$ | ${\color{red}7}$ | $ 7 \times 1 = 7$ |
$5\times 2 = {\color{green}10}$ | ${\color{green}10} +{ \color{#cccc00}4}$ | ${\color{red}14}$ | $7 \times 2 = 14$ |
| $5\times 3 = {\color{green}15}$ | ${\color{green}15} +{ \color{#cccc00}6}$ | ${\color{red}21}$ | $7 \times 3 = 21$ |
$5\times 4 = {\color{green}20}$ | ${\color{green}20} +{ \color{#cccc00}8}$ | ${\color{red}28}$ | $7 \times 4 =28$ |
| $5\times 5 = {\color{green}25}$ | ${\color{green}25} +{ \color{#cccc00}10}$ | ${\color{red}35}$ | $7 \times 5 =35$ |
$5\times 6 = {\color{green}30}$ | ${\color{green}30} +{ \color{#cccc00}12}$ | ${\color{red}42}$ | $7 \times 6 =42$ |
| $5\times 7 = {\color{green}35}$ | ${\color{green}35} +{ \color{#cccc00}14}$ | ${\color{red}49}$ | $7 \times 7 = 49$ |
$5\times 8 = {\color{green}40}$ | ${\color{green}40} +{ \color{#cccc00}16}$ | ${\color{red}56}$ | $7 \times 8 = 56$ |
| $5\times 9 = {\color{green}45}$ | ${\color{green}45} +{ \color{#cccc00}18}$ | ${\color{red}63}$ | $7 \times 9 = 63$ |
$5\times 10 = {\color{green}50}$ | ${\color{green}50} +{ \color{#cccc00}20}$ | ${\color{red}70}$ | $7 \times 10 = 70$ |
Paired Tables: This method involves using paired tables and is only effective if the students have learned and memorized all the previous tables by heart. This method is the quickest method to learn the 7 times table, but it works only for the first six multiples of 7.
We know that $7\times 1 =7 $ and $1\times 7$ is also equal to 7. Similarly, $7\times 2 =14$ and $2\times 7 = 14$. So, if we have memorized the previous tables, then we can draw a paired table of 7 up to $7 \times 6$, as shown below.
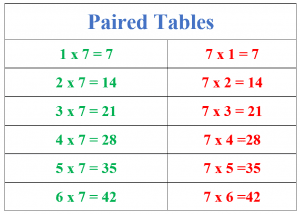
Using this method, students will quickly learn the 7 times table up to the sixth multiple of 7 and memorize the rest of the multiples separately.
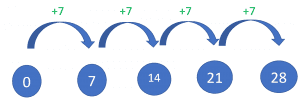
- Addition: This is an easy and effective method, and this method can be used to learn any table, but the downside is that this method is lengthy, tedious, and the calculations take time. This method is good if students want to learn and memorize the first 10 multiples of 7.
Students can use this method along with the recitation of the 7 times table to help them memorize the table quickly. As the name suggests, this method involves simple addition.
For example, we start with digit 0, and if we add the number 7 to it, we get the first multiple of 7. Now, we can work out the next multiple of 7 by adding 7 to the previous multiple and so on.
- Recitation: This is the most popular adopted method in schools to help students memorize the 7 times table. If students have difficulty grasping previous tips and tricks to learn the 7 times table, they can use this method. Students can recite the 7 times table loudly and repeatedly. Once they have memorized it, it will be easier for them to develop their basic understanding.
Recitation can be done like:
- Seven times one is 7
- Seven times two is 14
- Seven times three is 21
- Seven Times four is 28
- Seven times five is 35
- Seven times six is 42
- Seven times seven is 49
- Seven times eight is 56
- Seven times nine is 63
- Seven times ten is 70
Table of 7 from 1 to 20:
We can write a complete table of 7 from 1 to 20 as:
Numerical Representation | Descriptive Representation | Product (Answer) |
$7 \times 1$ | Seven times one | $7$ |
| $7 \times 2$ | Seven times two | $14$ |
$7 \times 3$ | Seven times three | $21$ |
| $7 \times 4$ | Seven times four | $28$ |
$7 \times 5$ | Seven times five | $35$ |
| $7 \times 6$ | Seven times six | $42$ |
$7 \times 7$ | Seven times seven | $49$ |
| $7 \times 8$ | Seven times eight | $56$ |
$7 \times 9$ | Seven times nine | $63$ |
| $7\times 10$ | Seven times ten | $70$ |
$7\times 11$ | Seven times eleven | $77$ |
| $7\times 12$ | Seven times twelve | $84$ |
$7\times 13$ | Seven times thirteen | $91$ |
| $7 \times 14$ | Seven times fourteen | $98$ |
$7 \times 15$ | Seven times fifteen | $105$ |
| $7 \times 16$ | Seven times sixteen | $112$ |
$7 \times 17$ | Seven times seventeen | $119$ |
| $7 \times 18$ | Seven times eighteen | $126$ |
$7 \times 19$ | Seven times nineteen | $133$ |
| $7 \times 20$ | Seven times twenty | $140$ |
Example 1: Calculate 7 times 1 times 7 minus 20
Solution:
7 times 1 times 7 minus 20 can be written as:
$ 7\times1 \times 7 – 20$
$ = 7\times 7 – 20$
$ = 49 – 20$
$ = 29$
Example 2: What is the 6th multiple of 7?
Solution:
We know the first 10 multiples of 7 are 7, 14, 21, 28, 35, 42, 49, 56, 63, and 60.
So, the 6th multiple is 42.
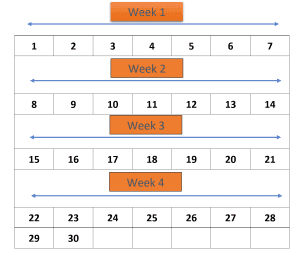
Example 3: Using the 7 times table, calculate the number of weeks in a month.
Solution:
We know that a month can contain a minimum of 28 and a maximum of 31 days.
We know the first 5 multiples of the number 7 are 7, 14, 21, 28, and 35. So, the 4th multiple is 28, so a month contains 4 weeks.
Practice Questions:
- Eve works 4 days a week. Using the 7 times table, determine how many days does she work in 7 weeks?
- Calculate 7 times 2 minus 10 times 7?
- Find the value of “Y” if “Y x 7 = 63”.
- From the given table, select the numbers which are multiples of 7
| 7 | 21 | 36 | 35 | 45 |
| 15 | 19 | 14 | 12 | 10 |
| 16 | 11 | 28 | 17 | 15 |
| 30 | 37 | 09 | 16 | 29 |
| 31 | 63 | 70 | 25 | 84 |
| 32 | 44 | 42 | 49 | 80 |
| 77 | 73 | 71 | 74 | 65 |
| 37 | 57 | 54 | 55 | 51 |
| 105 | 82 | 72 | 51 | 65 |
| 44 | 48 | 56 | 89 | 60 |
Answer Key
1) Eve works 4 days a week. A week contains 7 days. So total number of working days in 7 weeks
$4\times 7 =28$ days.
2) 10 times 7 minus 2 times 7 can be written as:
$ 10\times 7 – 2\times 7$
$ = 70 – 14$
$ = 56$
3) $ Y \times 7 = 63 $
We know $7\times 9 =63$, so
$ Y = 9 $.
4)
| 7 | 21 | 36 | 35 | 45 |
| 15 | 19 | 14 | 12 | 10 |
| 16 | 11 | 28 | 17 | 15 |
| 30 | 37 | 09 | 16 | 29 |
| 31 | 63 | 70 | 25 | 84 |
| 32 | 44 | 42 | 49 | 80 |
| 77 | 73 | 71 | 74 | 65 |
| 37 | 57 | 54 | 55 | 51 |
| 105 | 82 | 72 | 51 | 65 |
| 44 | 48 | 56 | 89 | 60 |