- Home
- >
- 8 times table – Explanation & Examples
JUMP TO TOPIC
8 times table – Explanation & Examples
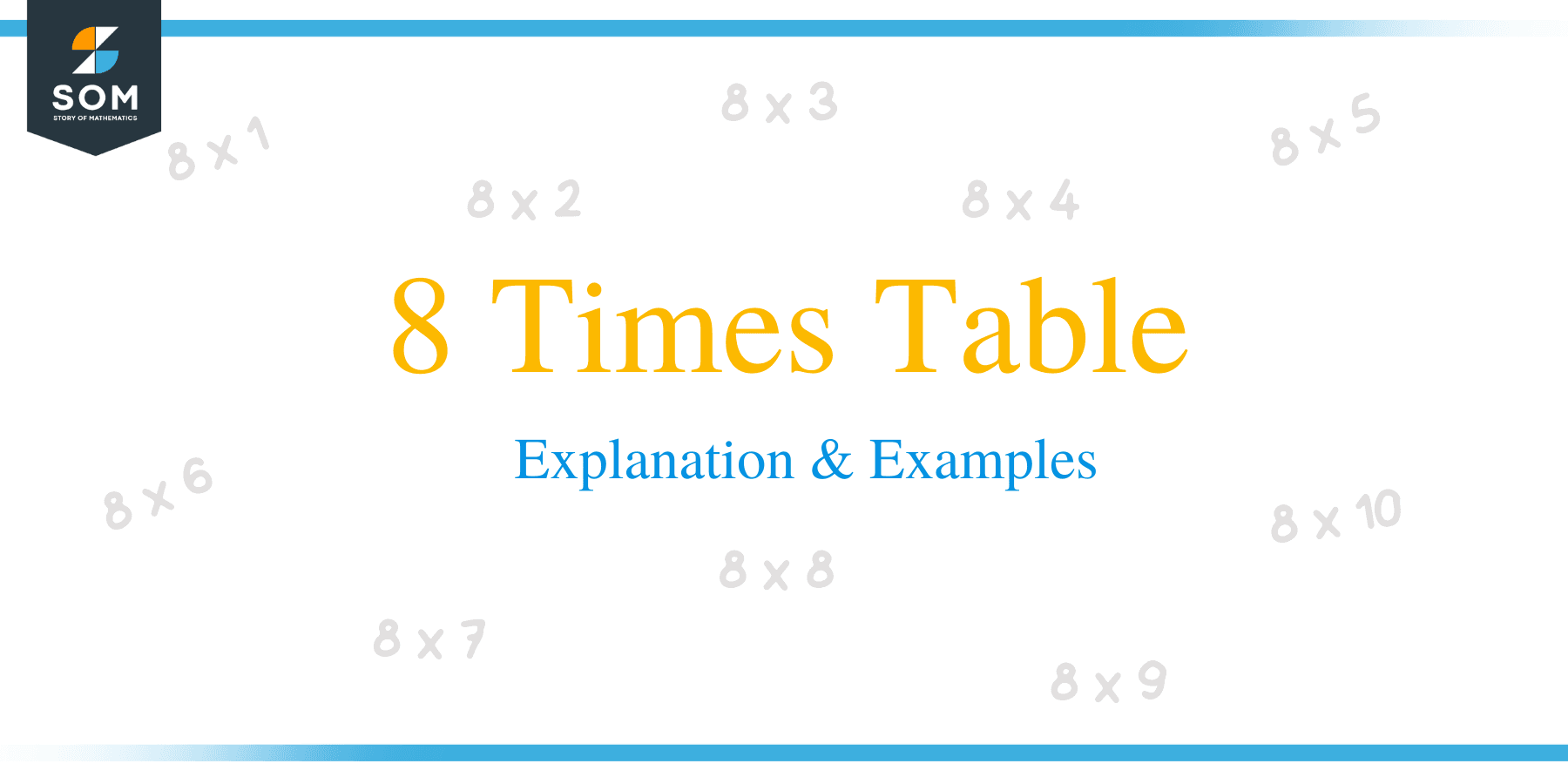 8 times table is one of the most important tables in mathematics. Learning 8 times table help students to feel positive about their mathematics and memorizing skills. Like 7 times table, this table is also hard to memorize.
8 times table is one of the most important tables in mathematics. Learning 8 times table help students to feel positive about their mathematics and memorizing skills. Like 7 times table, this table is also hard to memorize.
8 times table is a table that presents multiples of 8 in a tabular form.
Learning and understanding the 8 times table is essential for solving the multiplication, division, L.C.M, H.C.F, and factorization-related mathematical problems. 8 times table does follow a certain pattern, but it is still hard to memorize. This topic will present some tips and techniques that will help students learn and memorize the 8 times table.
Children should refresh the following concepts to understand the material discussed in this topic.
- Basics of addition and multiplication.
- Maths table 1 to 7
8 multiplication table
We can write the table of as:
- $8 \times1 = 8$
- $8 \times 2 = 16$
- $8 \times 3 = 24$
- $8 \times 4 =32$
- $8 \times 5 =40$
- $8 \times 6 =48$
- $8 \times 7 = 56$
- $8 \times 8 = 64$
- $8 \times 9 = 72$
- $8 \times 10 = 80$
Different tips for 8 times table:
Let us discuss some of the tips and tricks that will help students quickly learn and memorize this table.
Digits Pattern: The last digit of the first five multiples of number 8 follow the pattern of 8,6,4,2 and 0, respectively. The same pattern is followed by the next 5 multiples and so on. This pattern can help students in quick memorization of this table. The pattern is highlighted in the picture below.

Using 7 Times table: This method is straightforward and effective in learning 8 times tables. This method also helps in the revision of the 7 times table. In this method, we add natural numbers in ascending order to multiples of the number 8, as shown in the table below. These natural numbers are the same numbers multiplied by 7 and are shown in the same red color in the table below. The first multiple of the number 7 is added with a first natural number, i.e., 1. Similarly, the second multiple of number 7 is added with a second natural number, i.e., 2, and so on. The detailed method is presented in the table below.
Seven Times Table | Addition | (Addition Outcome) | Eight Times Table |
7 x 1 = 7 | 7 + 1 | 8 | 8 x 1 = 8 |
7 x 2 = 14 | 14 + 2 | 16 | 8 x 2 = 16 |
7 x 3 = 21 | 21 + 3 | 24 | 8 x 3 = 24 |
7 x 4 = 28 | 28 + 4 | 32 | 8 x 4 =32 |
7 x 5 = 35 | 35 + 5 | 40 | 8 x 5 =40 |
7 x 6 = 42 | 42 + 6 | 48 | 8 x 6 =48 |
7 x 7 = 49 | 49 + 7 | 56 | 8 x 7 = 56 |
7 x 8 = 56 | 56 + 8 | 64 | 8 x 8 = 64 |
7 x 9 = 63 | 63 + 9 | 72 | 8 x 9 = 72 |
7 x 10 = 70 | 70 + 10 | 80 | 8 x 10 = 80 |
Using 4 times table: This method is simple and will help students revise 4 times table. If we double the answers/ multiples of 4 times table, then the resulting multiples/ answers will form an 8 times table. For example, 4\ times 3 =12 if we double up the answer 12 to 24, then it is the same as 8\ times 3 = 24. Method implementation is presented in the table below.
Four Times Table | Double the Answer | Multiples of 8 |
4 x 1 = 4 | 4 + 4 | 8 |
4 x 2 = 8 | 8 + 8 | 16 |
4 x 3 = 12 | 12 + 12 | 24 |
4 x 4 = 16 | 16 + 16 | 32 |
4 x 5 = 20 | 20 + 20 | 40 |
4 x 6 = 24 | 24 + 24 | 48 |
4 x 7 = 28 | 28 + 28 | 56 |
4 x 8 = 32 | 32 + 32 | 64 |
4 x 9 = 36 | 36 + 36 | 72 |
4 x 10 = 40 | 40 + 40 | 80 |
Addition: This is a universal method that can be applied to any table. It is an easy and effective method to help students learn and memorize the tables, and it also improves their addition skills. The only downside is that this method is lengthy and time-consuming.
Recitation: This method is for those students who have difficulty understanding previous tips, basic addition, and multiplication. Students can recite the 8 times loudly and repeatedly to help them memorize the table, and after that, they can focus on learning the other tips and skills to help them understand the table. Recitation can be done like
- Eight times one is 8
- Eight times two is 16
- Eight times three is 24
- Eight times four is 32
- Eight times five is 40
- Eight times six is 48
- Eight times seven is 56
- Eight times eight is 64
- Eight times nine is 72
- Eight times ten is 80
Table of 8 from 1 to 20:
We can write a complete table of 8 from 1 to 20 as:
Numerical Representation | Descriptive Representation | Product (Table Outcome) |
$8 \times 1$ | Eight times one | 8 |
$8 \times 2$ | Eight times two | 16 |
$8 \times 3$ | Eight times three | 24 |
$8 \times 4$ | Eight times four | 32 |
$8 \times 5$ | Eight times five | 40 |
$8 \times 6$ | Eight times six | 48 |
$8 \times 7$ | Eight times seven | 56 |
$8 \times 8$ | Eight times eight | 64 |
$8 \times 9$ | Eight times nine | 72 |
$8\times 10$ | Eight times ten | 80 |
$8\times 11$ | Eight times eleven | 88 |
$8\times 12$ | Eight times twelve | 96 |
$8\times 13$ | Eight times thirteen | 104 |
$8 \times 14$ | Eight times fourteen | 112 |
$8 \times 15$ | Eight times fifteen | 120 |
$8 \times 16$ | Eight times sixteen | 128 |
$8 \times 17$ | Eight times seventeen | 136 |
$8 \times 18$ | Eight times eighteen | 144 |
$8 \times 19$ | Eight times nineteen | 152 |
| $8 \times 20$ | Eight times twenty | 160 |
This table shows the pattern of 8,6,4,2, and 0 is followed after every 5 multiples of 8. Students can use this pattern method to help them in multiplication problems as well.
Example 1: Calculate 8 times 4 times 2 plus 6
Solution:
8 times 4 times 2 plus 6 can be written as:
$ = 8\times 4 \times 2 + 6$
$ = 32\times 2 + 6$
$ = 64 + 6$
$ = 70$
Example 2: Find the value of “Y” if “$8Y + 8 = 88$”
Solution:
$ 8Y + 8 = 88 $
$ 8Y = 88 – 8 $
$ 8Y = 80 $
$Y = \frac{80}{8}$. We know $8\times 10 =80$
$ Y = 10 $.
Example 3: Alex’s job hours are from 09:00 to 05:00. Alex is paid 2 dollars for 1 hour. Calculate the amount earned if
- Alex works for 2 days
- Alex works for a whole week
- Alex works for five days
Solution:
1. Alex’s job hours are from 09:00 to 05:00 hrs. So, Alex works 8 hours a day. If Alex works for 2 days, then by using the 8 times table, we know his total working hours are $8 \times 2 = 16$ hours. Alex is paid 2 dollars for 1 hour. So, the total amount earned $2 \times 16 = 32$ dollars.
2. If Alex works for a whole week, then his cumulative job hours are
$8\times 7 = 56$ hours.
So, total Amount earned by Alex is $2 \times 56 = 112$ dollars
3. If Alex works for 5 days, then his cumulative job hours are
$8 \times 5 = 40$ hours.
So, the total amount earned by Alex is $2\times 40 = 80$ dollars.
Practice Questions:
- If a single box can contain 8 balls in it. Calculate the total amount of balls in four boxes.
- Calculate 8 times 8 minus 2 times 6?
- Find the value of “Y” if “$16Y + ( 8 \times 6) = 64$”
- From the given table, select the numbers which are multiples of 8
| 13 | 21 | 29 | 19 | 65 | 61 |
| 23 | 19 | 17 | 09 | 10 | 63 |
| 16 | 80 | 28 | 57 | 95 | 105 |
| 30 | 37 | 35 | 59 | 79 | 111 |
| 31 | 63 | 70 | 36 | 88 | 160 |
| 33 | 64 | 42 | 49 | 70 | 99 |
| 72 | 73 | 71 | 74 | 105 | 104 |
| 37 | 57 | 56 | 59 | 51 | 136 |
| 115 | 82 | 96 | 51 | 65 | 145 |
| 49 | 48 | 40 | 89 | 90 | 134 |
Answer Key
1.We know that a single box contains 8 balls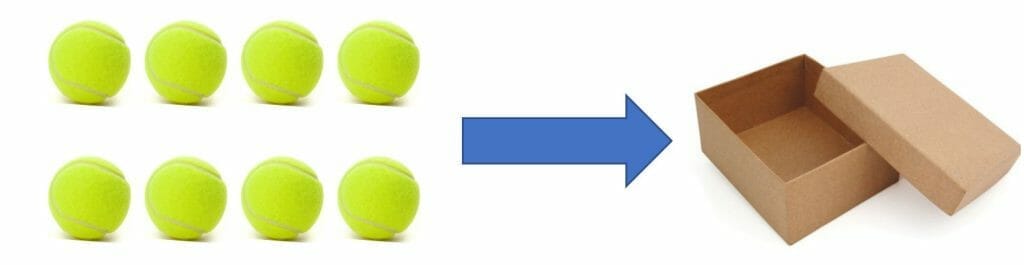 So, if we have four boxes, then the total amount of balls can be calculated using 8 times table.$= 8 \times 4 = 32$ balls.
So, if we have four boxes, then the total amount of balls can be calculated using 8 times table.$= 8 \times 4 = 32$ balls.
2.8 times 8 minus 2 times 6 can be written as:
$ = 8\times 8 – 2 \times 6$
$ = 64 – 12 $
$ = 52$
3. $16Y + ( 8 \times 6) = 64$
$ = 16Y+ 48 = 64 $
$ 16Y = 64 – 48 $
$ 16Y = 16 $
$Y = \frac{16}{16}$.
$ Y = 1 $.
4.
| 13 | 21 | 29 | 19 | 65 | 61 |
| 23 | 19 | 17 | 09 | 10 | 63 |
| 16 | 80 | 28 | 57 | 95 | 105 |
| 30 | 37 | 35 | 59 | 79 | 111 |
| 31 | 63 | 70 | 36 | 88 | 160 |
| 33 | 64 | 42 | 49 | 70 | 99 |
| 72 | 73 | 71 | 74 | 105 | 104 |
| 37 | 57 | 56 | 59 | 51 | 136 |
| 115 | 82 | 96 | 51 | 65 | 145 |
| 49 | 48 | 40 | 89 | 90 | 134 |
