
The particle moves from the origin O to a final position with the coordinates as x=4.65m and y=4.65m, which is also represented in the following figure.
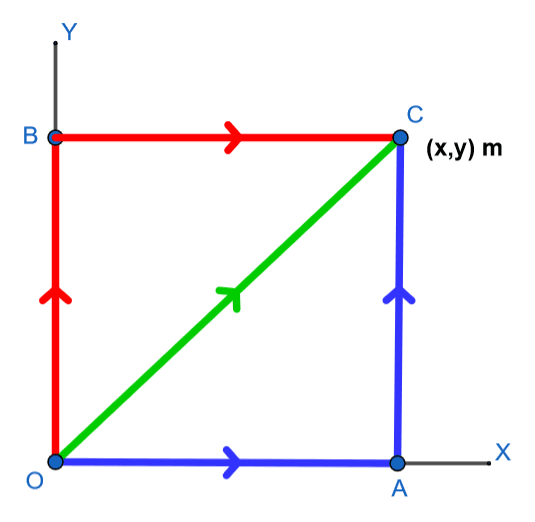
Figure 1
- Find work done by F along OAC
- Find work done by F along OBC
- Find work done by F along OC
- Is F conservative or non-conservative?
This problem aims to find the work done by the particle moving in the xy plane as it moves to the new position with the given coordinates. The concepts required for this problem are related to basic physics, which includes work done on a body and friction force.
The concept of work done comes as the dot product of the horizontal component of the force with the direction of the displacement along with the value of the displacement.
\[ F_s = F_x = Fcos \theta \space s \]
The component that is responsible for the movement of the object is $Fcos\theta$, where $\theta$ is the angle between the force $F$ and the displacement vector $s$.
Mathematically, Work done is a scalar quantity and is expressed as:
\[ W = F \times s = (Fcos \theta) \times s \]
Where $W=$ work, $F=$ force exerted.
Expert Answer
Part A:
Work done by $F$ along $OAC$
We are given the following information:
Force $F = (2y i + x^2 j) N$,
The displacement in the direction of $x = 4.65 m$ and
The displacement in the direction of $y = 4.65 m$.
To calculate the work done, according to the given figure we are going to use the formula:
\[W=\dfrac {1}{2} \times\ x \times y\]
\[W=\dfrac {1}{2} \times\ 4.65 \times 4.65\]
\[W=\dfrac {1}{2} \times\ 21.6225\]
\[W= 10.811 \space J\]
Part B:
Work done by $F$ along $OBC$
Force $F = (2y i + x^2 j) N$,
The displacement in the direction of $x = 4.65 m$ and
The displacement in the direction of $y = 4.65 m$.
\[W=\dfrac{1}{2} \times\ x \times y\]
\[W=\dfrac{1}{2} \times\ 4.65 \times 4.65 \]
\[W=\dfrac{1}{2} \times\ 21.6225 \]
\[W=10.811 \space J\]
Part C:
Work done by $F$ along $OC$
We are given the following information:
Force $F = (2y i + x^2 j) N$,
The displacement in the direction of $x = 4.65 m$ and
The displacement in the direction of $y = 4.65 m$.
The position of particle at the point $C = (4.65 i+4.65 j)$
To calculate the work done we are going to use the formula:
\[W_{particle}=F \times s = (2y i + x^2 j)(4.65 i+4.65 j)\]
\[W_{particle}=(2(4.65) i + (4.65)^2 j) (4.65 i+4.65 j)\]
\[W_{particle}=143.78\space J\]
Part D:
Non-conservative Force
Numerical Result
Part A: $10.811\space J$
Part B: $10.811\space J$
Part C: $143.78\space J$
Part D: Non-conservative Force
Example
Find the work done in driving a cart via a distance of $50 m$ against the force of friction of $250N$. Also, comment on the kind of work done.
We are given:
The Force exerted $F=250N$
Displacement $S=50m$
\[ W=F\times S\]
\[W=250\times50\]
\[W=1250\space J\]
Note that the work done here is negative.
Image/Mathematical drawings are created in Geogebra.
