
This question widely explains the concept of the sampling distribution of sample proportions.
The population proportion plays an important role in many areas of science. This is because research questionnaires in many fields involve this parameter. The success proportion is calculated by the sampling distribution of sample proportions. It is the ratio of the chance of occurrence of some event, say $x$, by the sample size, say $n$. Mathematically, it is defined as $\hat{p}=\dfrac{x}{n}$. Assume a qualitative variable and let $p$ be the proportion in the category taken if the repeated random samples of size $n$ are drawn from it, the population proportion $p$ equals the mean of all the sample proportions denoted by $\mu_\hat{p}$.
In terms of the spread of all sample proportions, theory dictates the behavior much more precisely than simply stating that larger samples have less spread. Indeed, the standard deviation of all sample proportions is proportional to the sample size $n$ in a manner that: $\sigma_{\hat{p}}=\sqrt{\dfrac{p(1-p)}{n}}$.
Because the sample size $n$ shows up in the denominator, the standard deviation decreases with the increase in sample size. Ultimately, as long as the sample size $n$ is large enough, the shape of the $\hat{p}$ distribution will be approximately normal with a condition that both $np$ and $n(1 – p)$ must be greater than or equal to $10$.
Expert Answer
The sample proportion is given by:
$\hat{p}=\dfrac{x}{n}$
Here, $x=86$ and $n=100$, so that:
$\hat{p}=\dfrac{86}{100}=0.86$
Let $p$ be the population proportion, then:
$p=90\%=0.09$
And $\mu_{\hat{p}}$ be the mean of the sample proportion then:
$\mu_{\hat{p}}=p=0.90$
Also, the standard deviation is given by:
$\sigma_{\hat{p}}=\sqrt{\dfrac{p(1-p)}{n}}$
$=\sqrt{\dfrac{0.90(1-0.90)}{100}}=0.03$
Now, find the required probability as:
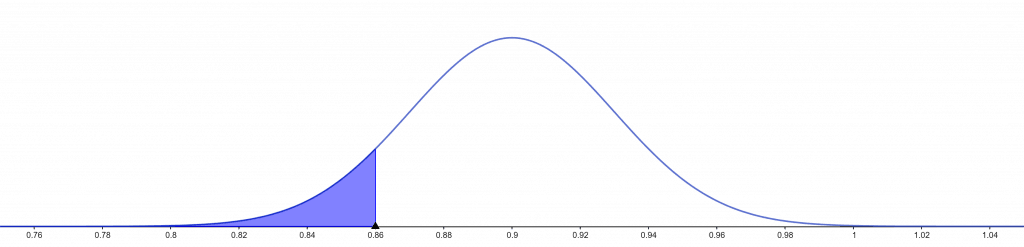
$P(\hat{p}\leq 0.86)=P\left(z\leq \dfrac{\hat{p}-\mu_{\hat{p}}}{\sigma_{\hat{p}}}\right)$
$=P\left(z\leq\dfrac{0.86-0.90}{0.03}\right)$
$=P(z\leq -1.33)$
$=0.0918$
Example
According to a retailer, $80\%$ of all orders are delivered within $10$ hours of being received. A customer placed $113$ orders of various sizes and at different times of the day; $96$ orders were dispatched within $10$ hours. Assume the retailer’s claim is correct, and calculate the likelihood that a sample of size $113$ would yield a sample proportion as small as that noticed in this sample.
Solution
Here, $x=96$ and $n=113$
So, $\hat{p}=\dfrac{x}{n}=\dfrac{96}{113}$
$\hat{p}=0.85$
Also, $\mu_{\hat{p}}=p=0.80$ and the standard deviation is:
$\sigma_{\hat{p}}=\sqrt{\dfrac{p(1-p)}{n}}$
$=\sqrt{\dfrac{0.80(1-0.80)}{113}}=0.04$
Now, find the required probability as:
$P(\hat{p}\leq 0.86)=P\left(z\leq \dfrac{\hat{p}-\mu_{\hat{p}}}{\sigma_{\hat{p}}}\right)$
$=P\left(z\leq\dfrac{0.85-0.80}{0.04}\right)$
$=P(z\leq 1.25)$
$=0.8944$
