A steel cylinder has a length of 2.16 in, a radius of 0.22 in, and a mass of 41 g. What is the density of the steel in g/cm^3?

This question aims to find the density of the cylinder walls. 

A solid three-dimensional shape made up of two parallel bases connected by a curved surface is called a cylinder. Both of the bases are shaped like circular discs. The axis of the cylinder is defined as the line that runs from the center or connects the centers of two circular bases. The capacity of a cylinder to hold an amount of material is determined by the volume of the cylinder. It is calculated by using a specific formula.

A cylinder’s volume is the number of cubic units that can fit inside it. In other words, it can be regarded as the space occupied by the cylinder since the volume of any three-dimensional shape is the space occupied by it. Several measurements can be taken out from a cylinder such as radius, volume, and height. The radius and height of a cylinder are used to calculate its surface area and volume. The height of both the oblique and right cylinders can be calculated by the means of the distance between two bases. This height is measured directly from one point on the top base to the same point directly below on the bottom base for a right cylinder. Also, the density of the cylinder is the mass of a substance per unit volume and is denoted by $\rho$.

Expert Answer

Since the density is given by:

Density $(\rho)=\dfrac{Mass}{Volume}$

Here, Mass $=41\,g$, and the volume is given by:

Volume $(V)=\pi r^2h$

where $r=0.22\,in$ and $h=2.16\,in$, therefore:

Volume $(V)=\pi (0.22\,in)^2(2.16\,in)$

$V=0.3284\,in^3$

Now since $1\,in=2.54\,cm$, so the volume becomes:

$V=0.3284(2.54\,cm)^3$

$V=5.3815\,cm^3$

And so:

$\rho=\dfrac{41\,g}{5.3815\,cm^3}$

$=7.62\,\dfrac{g}{cm^3}$

Example 1

Find the volume of the cylinder in cubic centimeters if its radius is $4\,cm$ and the height is $7.5\,cm$.

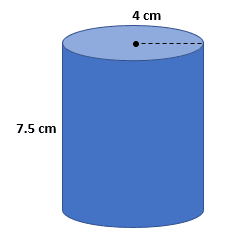
Solution

Let $V$ be the volume, $h$ be the height and $r$ be the radius of the cylinder then:

$V=\pi r^2h$

where:

$r=4\,cm$ and $h=7.5\,cm$

So, $V=\pi(4\,cm)^2(7.5\,cm)$

$V\approx 377\,cm^3$

Example 2

Consider a cylinder having the volume $23\,cm^3$ and height $14\,cm$. Find its radius in inches.

Solution

Since $V=\pi r^2h$

Also given that:

$V=23\,cm^3$ and $h=14\,cm$

Substituting $V$ and $h$ we get:

$23\,cm^3=\pi r^2 (14\,cm)$

$\pi r^2=1.6429\,cm^2$

$r^2=\dfrac{1.6429\,cm^2}{\pi}$

$=0.5229\,cm^2$

$r=0.7131\,cm$

Now, since $1\,cm=0.393701\,in$

Therefore the radius in inches is given by:

$r=(0.7131)(0.393701\,in)$

$r=0.28075\,in$

Previous Question < > Next Question