- Home
- >
- Absolute maximum – Definition, Conditions, and Examples
JUMP TO TOPIC
Absolute maximum – Definition, Conditions, and Examples
 Learning about a function’s absolute maximum will help us in sketching the function’s graphs accurately. The absolute maximum is an important component of a function. In fact, this comes in handy when we solve optimization problems: optimizing the profit, finding the highest point, and the largest area covered.
Learning about a function’s absolute maximum will help us in sketching the function’s graphs accurately. The absolute maximum is an important component of a function. In fact, this comes in handy when we solve optimization problems: optimizing the profit, finding the highest point, and the largest area covered.
The function’s absolute maximum represents the function’s maximum value within a given interval or throughout its domain. A function can only have one absolute maximum.
Since absolute maximum is an application of first and second derivative tests, make sure that you have your notes handy. You can also check out this article in case you need a refresher.
In this article, we’ll show you what makes an absolute maximum different from a local maximum. We’ll also try out problems that involve the function’s absolute maximum.
What is an absolute maximum?
The absolute maximum (or also known as global maximum) of a function, $f(x)$, represents that highest possible values for $f(x)$.Let’s say we have the function’s critical number, $x =c$, within its domain. The function $f(x)$ is said to have an absolute maximum at $x= c$ if it satisfies the inequality shown below.
\begin{aligned}f(c) \geq f(x)\\ x \in \text{ Domain}\end{aligned}
When this is true, $\boldsymbol{(c, f(x))}$ is the absolute maximum and the highest possible values for $f(x)$ is $\boldsymbol{f(c)}$.
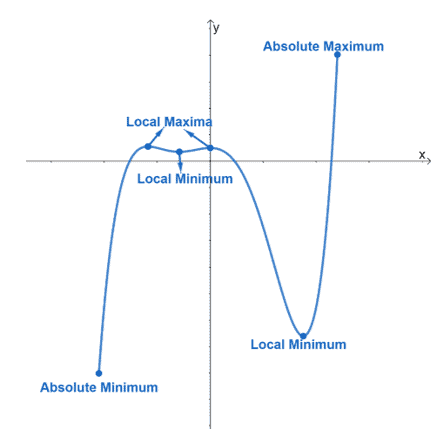
Here’s a graph showing you the curve’s different extrema. As you can see from the graph, a function can have one or more local minima or extrema. The function, however, will only have one absolute maximum (and minimum).
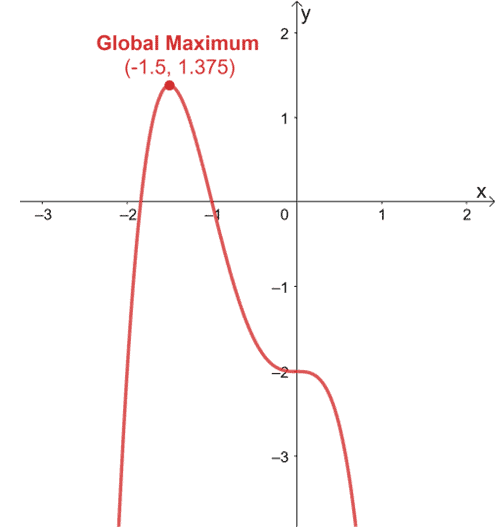
This function, for example, has a global maximum (or the absolute maximum) at $(-1.5, 1.375)$. This means that the highest value of the function is $1.375$. Let’s say this graph represents the motion of an object. This means that the function reaches the highest point of $1.375$ units.
How to find the absolute maximum?
By inspection, we can find the absolute maximum by looking for the highest point of the function’s curve. We’ll show you three common conditions that you might encounter in your Calculus classes:
- Finding the absolute maximum (also known as the global maximum) through the domain of the function, $(-\infty, \infty)$.
- Finding one global maximum within a closed interval.
- Finding multiple absolute maximum points – this normally occurs in periodic functions such as $y =\cos x$.
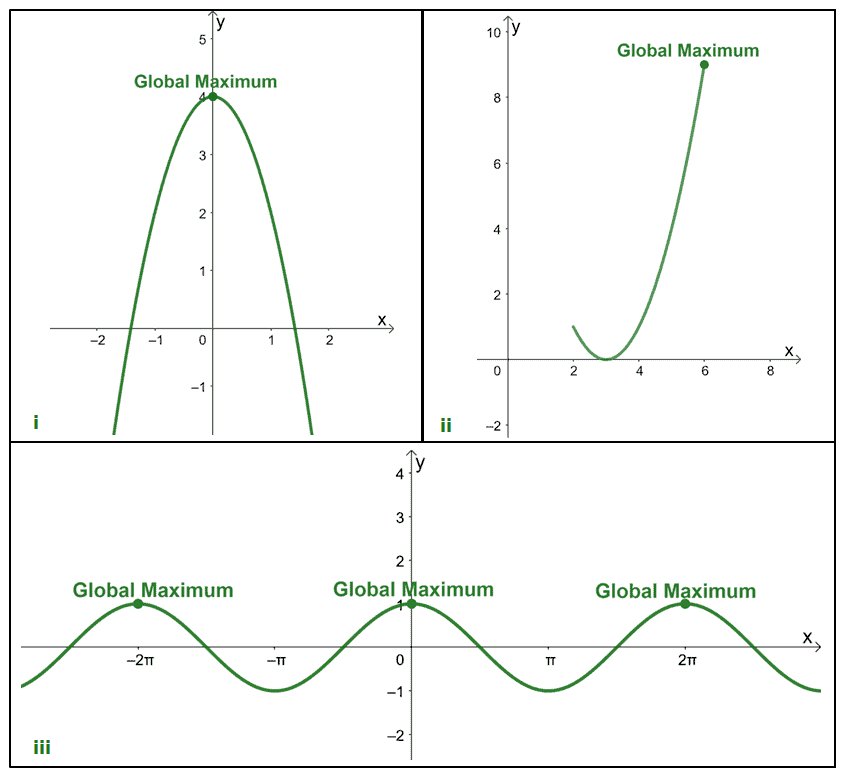
For each case, make sure to find the highest point/s of the function. The value of the function there represents its absolute or global maximum.
- The function’s highest point is $(0, 4)$ throughout its domain, $(-\infty, \infty)$. This means that the function’s absolute maximum is $4$.
- Within the interval of $[2, 6]$, the function has a maximum value at $(6, 9)$, so the function has a global maximum of $6$.
- We can see the highest points ay $(-2\pi, 1)$, $(0, 1)$, and $(2\pi, 1)$. This shows that a function may have multiple maximum points, but it will still have one global maximum: $1$.
What if we’re not given the function’s graph? We can still find the function’s global maximum using the Extreme Value Theorem. When $f(x)$ is continuous on the interval, $[a, b]$,$f(x)$ should have absolute maximum within the given interval.
Here are the steps to keep in mind when finding the function’s absolute maximum:
- Make sure that the function is continuous within the interval.
- Find the critical numbers of the function within the interval. Recall that we can find the critical numbers of $f(x)$ by equating $\boldsymbol{f^{\prime}(x)}$ to zero.
- Evaluate $f(x)$ at the critical numbers and the endpoints. Whichever is the highest value of $\boldsymbol{f(x)}$ represents the function’s global or absolute maximum.
Let’s say we want to find the absolute maximum of $f(x) = x^2$ within the interval, $[-3, 3]$. Since $f(x)$ is continuous within $[-3, 3]$, we can proceed and find its critical numbers. Find $f’(x)$ using the power rule and equating the resulting expression to $0$.
\begin{aligned}f^{\prime}(x) &= 2x^{2-1}, \phantom{x}\color{Green}\text{Power Rule}\\&=2x\\\\f^{\prime}(x)&=0\\2x &=0\\x&= 0\end{aligned}
Evaluate $f(x)$ at the critical point and the interval’s endpoints.
| \begin{aligned}\boldsymbol{x = -3 }\end{aligned} | \begin{aligned}\boldsymbol{x =0}\end{aligned} | \begin{aligned}\boldsymbol{x = 3 }\end{aligned} |
| \begin{aligned}f(-3) &= (-3)^2\\&= 9\end{aligned} | \begin{aligned}f(0) &= (0)^2\\&= 0\end{aligned} | \begin{aligned}f(3) &= (3)^2\\&= 9\end{aligned} |
The largest value for $f(x)$ occurs when $x = -3$ and $x = 3$, so the absolute maximum of $f(x)$ is $9$.
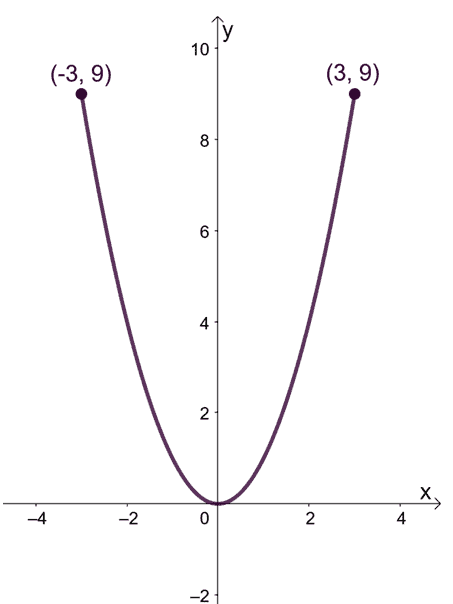
The graph shows the curve of $f(x)$ within the interval, $[-3, 3]$. We can see from this that the highest point of $f(x)$ is $9$, so this confirms what we currently know: $f(x)$’s global maximum is indeed equal to $9$.
We’ll approach a similar process when finding the absolute maxima of different functions. Try out the problems shown below once you’re ready!
Example 1
Use the graph of $h(x)$ to answer the questions that follow.
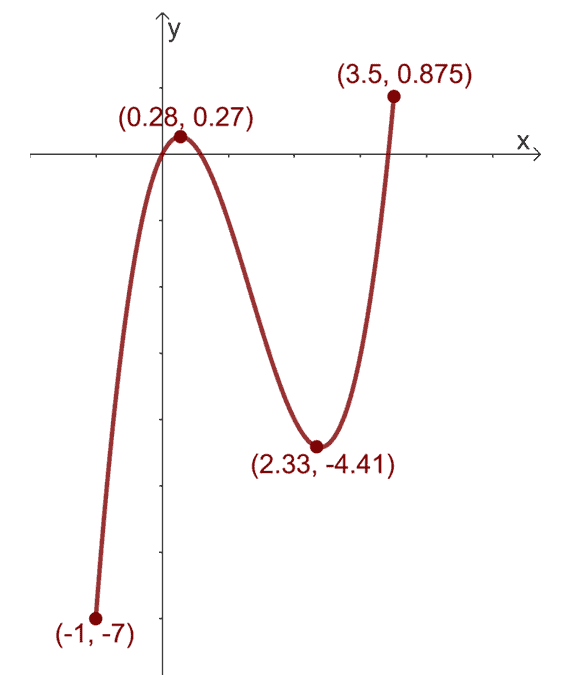
i) What is the interval covered by the graph shown above?
ii) What is the global maximum of the function?
iii) If $x = c$ is a critical point of $h’(x)$ and is within the interval of the curve, what can you say about $h(c)$ and $h(3.5)$?
Solution
The graph extends from $x=-1$ to $x = 3.5$, so the curve shown covers the interval, $[-1, 3.5]$.
Within the interval, $[-1, 3.5]$, we can see that the maximum value of $h(x)$ is $0.875$, so $h(x)$ has a global maximum of $0.875$.
This means that within the given interval, $h(3.5) = 0.875$ will be the highest point. Hence, $h(3.5)$ will always be greater than any value of $h(c)$ within the interval, $[-1, 3.5]$.
\begin{aligned}h(c) &\leq h(x)\end{aligned}
Example 2
Determine the absolute maximum of the function $g(x) = 3x + \dfrac{3}{x}$ over the interval, $[1, 4]$, if it exists.
Solution
The function $g(x)$ is continuous within the interval, $[1, 4]$. Let’s find the critical numbers of the function by finding $g^{\prime}(x)$.
\begin{aligned}g(x) &= 3x + \dfrac{3}{x}\\&=3\left(x + \dfrac{1}{x} \right )\\\\g^{\prime}(x)&=\dfrac{d}{dx} \left[3\left(x + \dfrac{1}{x} \right )\right]\\&= 3\dfrac{d}{dx} \left(x + \dfrac{1}{x} \right ), \phantom{x}\color{Green}\text{Constant Multiple Rule}\\&= 3{\color{Green}\left(\dfrac{d}{dx} x + \dfrac{d}{dx} \dfrac{1}{x} \right )}, \phantom{x}\color{Green}\text{Sum Rule}\\&= 3\left(\dfrac{d}{dx} x + \dfrac{d}{dx} x^{-1}\right)\\&= 3({\color{Green}1 -1x^{-2} }),\phantom{x}\color{Green}\text{Power Rule}\\&=3 -\dfrac{3}{x^2}\end{aligned}
Equate $g^{\prime}(x)$ to zero then find the critical numbers of $g(x)$ within the interval, $[1, 4]$.
\begin{aligned}g^{\prime}(x)&=0\\3 -\dfrac{3}{x^2}&= 0\\3x^2 -3&= 0\\3x^2 &= 3\\x^2 &= 1\\x&= \pm 1\end{aligned}
This means that within the given interval, we have a critical number at $x =1$. Now, let’s check the values of $g(x)$ at $x= 1$ and $x = 4$.
| \begin{aligned}\boldsymbol{x = 1 }\end{aligned} | \begin{aligned}\boldsymbol{x = 4}\end{aligned} |
| \begin{aligned}g(1) &= 3(1) + \dfrac{3}{1}\\&= 6\end{aligned} | \begin{aligned}g(4) &= 3(4) + \dfrac{3}{4}\\&= \dfrac{51}{4}\end{aligned} |
From the results, we can see that $g(x)$ has an absolute maximum of $\dfrac{51}{4}$.
Example 3
Determine the absolute maximum of the function $f(x) = \dfrac{-160x}{x^2 + 16}$ over the interval, $[0, 5]$, if it exists.
Solution
The denominator of $f(x)$ will always be greater than $0$, so $f(x)$ is continuous throughout the interval, $[0, 5]$.Now, differentiate $f(x)$ to begin our process of finding the function’s critical numbers.
\begin{aligned}f(x) &= \dfrac{-160x}{x^2 + 16}\\f^{\prime}(x) &= \dfrac{(x^2 + 16)\dfrac{d}{dx}(-160x) – (-160x)\dfrac{d}{dx}(x^2 + 16)}{(x^2 + 16)^2},\phantom{x}{\color{Green}\text{Quotient Rule}}\\&=\dfrac{(x^2 + 16){\color{Green}(-160)\left(\dfrac{d}{dx}x \right )} + (160x){\color{Green}\left(\dfrac{d}{dx}x^2 + \dfrac{d}{dx}16 \right )}}{(x^2 + 16)^2},\phantom{x}{\color{Green}\text{Constant Multiple & Sum Rules}}\\&= \dfrac{(x^2 + 16) (-160)({\color{Green}1})+ (160x)({\color{Green} 2x +0})}{(x^2 + 16)^2},\phantom{x}{\color{Green}\text{Power & Constant Rules}}\\&= \dfrac{-160(x^2 + 16)+160x(2x)}{(x^2 +16)^2}\\&= \dfrac{-160(x^2 +1 6)}{(x^2 +16)^2}\end{aligned}
Equate $f^{\prime}(x)$ to zero to find the $f(x)$’s critical numbers.
\begin{aligned}f^{\prime}(x) &=0 \\\dfrac{-160(x^2 +1 6)}{(x^2 +16)^2} &= 0\\-160(x^2 + 16)&= 0\\x^2 + 16 &= 0\\x^2 &= -16\end{aligned}
Since $x^2$ will always be positive, the equation has no solution. This means that we can’t find $f(x)$’s critical numbers. Instead, let’s observe the values of $f(x)$ at its interval’s endpoints.
| \begin{aligned}\boldsymbol{x = 0 }\end{aligned} | \begin{aligned}\boldsymbol{x = 5}\end{aligned} |
| \begin{aligned}f(0) &=\dfrac{-160(0)}{(0)^2 + 16}\\&= 0\end{aligned} | \begin{aligned}f(5) &=\dfrac{-160(5)}{(5)^2 + 16}\\&= \dfrac{-800}{41}\\&= -\dfrac{800}{41}\end{aligned} |
From this, we can see that $f(x)$’s global maximum for the interval $[0, 5]$ is $0$.
Example 4
Martha realized that its company’s weekly profit from the sale of $x$ units of office chairs can be modeled by the function, $P(x) = -0.04x^3 + 300x – 40000$. Their current production power can only manufacture a maximum of $120$ units each week. Their contracts with local shops require them to create at least $40$ units per week. What is the maximum possible profit that Martha’s company can make in a week?
Solution
The minimum number of office chairs that Martha’s company can make is $40$ while they can produce a maximum of $120$ units per week. This means that we’re finding the global maximum of $P(x) = -0.04x^3 + 432x – 40000$ within the interval, $[40, 120]$.
Let’s go ahead and find the critical numbers for $P(x)$. Find the values of $x$ that satisfy the equation, $P^{\prime}(x) = 0$.
\begin{aligned}P(x) &= -0.04x^3 + 300x – 40000\\P^{\prime}(x) &= \dfrac{d}{dx}(-0.04x^3 + 432x – 40000)\\&= \dfrac{d}{dx}-0.04x^3 + \dfrac{d}{dx}432x – \dfrac{d}{dx}40000,\phantom{x}{\color{Green}\text{Sum & Difference Rules}}\\&={\color{Green} -0.04\dfrac{d}{dx}x^3 + 432\dfrac{d}{dx}x} – \dfrac{d}{dx}40000,\phantom{x}{\color{Green}\text{Constant Multiple Rule}}\\&=-0.04{\color{Green}(3x^2)} +300{\color{Green}(1)} – {\color{DarkOrange} 0},\phantom{x}{\color{Green}\text{Power Rule}}\text{ & }{\color{DarkOrange}\text{Constant Rule}}\\&= -0.12x^2+432\end{aligned}
Equate this expression to $0$ then find the values of $x$.
\begin{aligned}P^{\prime}(x) &=0\\ -0.12x^2+432&= 0\\x^2 &= 3600\\x&= 60\end{aligned}
Disregard the negative root since $x$ represents the number of computer chairs, so $x$ will always be greater than zero. Evaluate $P(x)$ at $x=40$, $x=60$, and $x=140$.
| \begin{aligned}\boldsymbol{x = -3 }\end{aligned} | \begin{aligned}\boldsymbol{x =0}\end{aligned} | \begin{aligned}\boldsymbol{x = 3 }\end{aligned} |
| \begin{aligned}P(40) &= 240\end{aligned} | \begin{aligned}f(60) &= (0)^2\\&= 0\end{aligned} | \begin{aligned}f(3) &= (3)^2\\&= 140\end{aligned} |
Since $P(x)$ is highest when $x =40$, the maximum profit that Martha’s company can earn is $240$ dollars.
Practice Questions
1. Use the graph of $g(x)$ to answer the questions that follow.
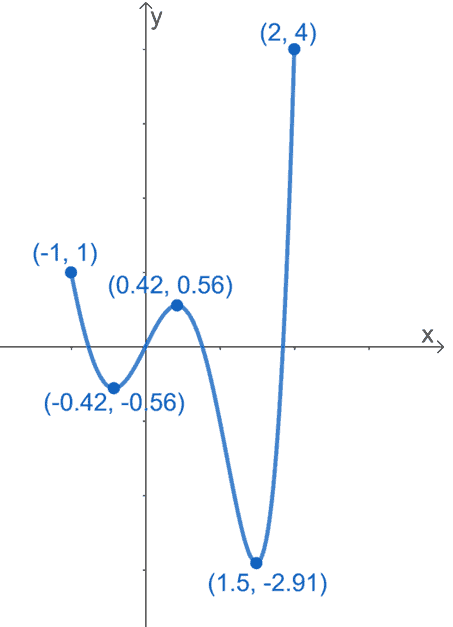
i) What is the interval covered by the graph shown above?
ii) What is the global maximum of the function?
iii) If $x = c$ is a critical point of $g’(x)$ and is within the interval of the curve, what can you say about $g(c)$ and $g(2)$?
2. Determine the absolute maximum of the function $h(x) = 4x + \dfrac{6}{x}$ over the interval, $[2, 6]$, if it exists.
3. Determine the absolute maximum of the function $f(x) = \dfrac{-250x}{x^2 + 25}$ over the interval, $[1, 6]$, if it exists.
Answer Key
1.
i) $[-1, 2]$
ii) $4$
iii)$g(c) \leq g(2)$
2. $25$
3. $-\dfrac{125}{13}$
Images/mathematical drawings are created with GeoGebra.
