Absolute minimum – Definition, Conditions, and Examples

The absolute minimum is an important component of a function, so it helps if you know how to find a function’s absolute minimum given its expression or graph. Absolute minimum is also useful in optimization problems: minimizing loss, finding the lowest point, and minimum population.

The function’s absolute minimum represents the function’s lowest value within a given interval or throughout its domain. There is only one absolute or global minimum for each function.

The absolute maximum and minimum are closely related to each other, so we’ll use the same concepts to find the function’s absolute minimum. In this article, we’ll show you the process of locating the function’s absolute minimum given its graph and function. We’ll also work on some word problems that involve a function’s minimum value.

What is an absolute minimum?

The absolute minimum, or also known as the global minimum, represents the lowest value possible for the function. Whether it’s throughout its domain or a given interval, a function will always have one unique absolute minimum.

The function $f(x)$ is said to have an absolute minimum at $x= c$ if it satisfies the inequality shown below.

\begin{aligned}f(c) \leq f(x)\\ x \in \text{ Domain}\end{aligned}

When a value satisfies this condition, $\boldsymbol{(c, f(x))}$ is the absolute minimum and the lowest possible values for $f(x)$ is $\boldsymbol{f(c)}$.

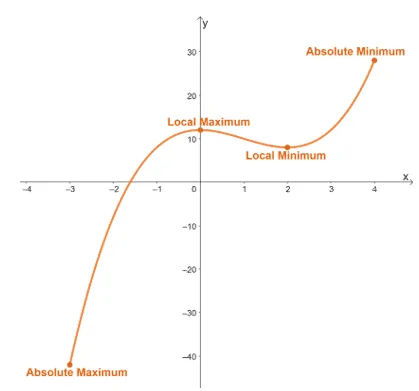
Here’s the graph of $y = x^3-3x^2 +12$ from $x = -3$ to $x = 4$. This shows that a function can have four extrema: local maximum, local minimum, absolute minimum, and absolute maximum. From this, we can see that the lowest possible value for the function is $-40$. This means that $y= x^3 – 3x^2 + 12$ has a global or absolute minimum of $-40$.

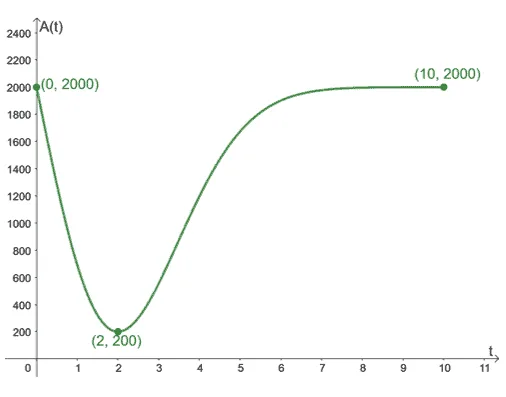
The graph above represents the amount, $A(t)$ in dollars, in the account throughout $t \in [0, 10]$ years. Since the lowest point of $A(t)$ is found at $(2, 200)$, this represents its global minimum for the interval, $[0, 10]$.

This means that the lowest amount in the account is $200$ dollars after having the account for $2$ years.

This is just one of the many applications of absolute minimum, so it’s important to know how to determine the function’s absolute minimum given its expression or graph.

How to find the absolute minimum?             

When given the graph of the function, it’s easy to spot its global minimum. We simply look out for the graph’s lowest point. These are three of the most common examples that you’ll encounter in your Calculus classes:

i) Finding the absolute minimum throughout the domain of the function, $(-\infty, \infty)$.
ii) Finding one absolute minimum within a closed interval.
iii) Working with periodic functions such as $y= \sin x$ and finding its global minimum.

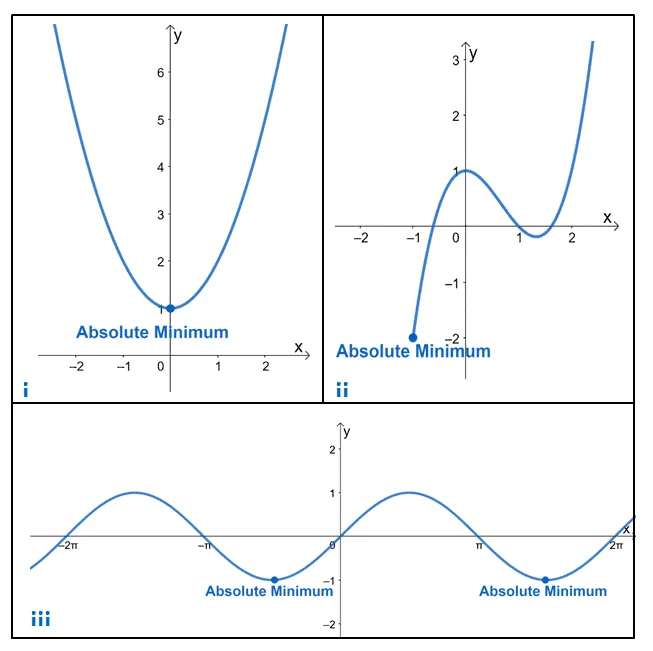
i) Finding the absolute minimum throughout the domain of the function, $(-\infty, \infty)$.
ii) Finding one absolute minimum within a closed interval.
iii) Working with periodic functions such as $y= \sin x$ and finding its global minimum.

Now, let’s move on to learning how to find the function’s absolute minimum given its expression. When $f(x)$ is a continuous function within the interval, $[a, b]$, it will contain an absolute minimum and maximum.

Keep these steps in mind when finding the function’s absolute minimum:

• Check that the function is continuous within the given interval.
• Find the critical numbers of the function that are within the given interval. Find the critical numbers of $f(x)$ by equating $\boldsymbol{f^{\prime}(x)}$ to zero.
• Evaluate $f(x)$ at the critical numbers and the endpoints. The lowest value returned will represent the function’s absolute minimum.

Use these guide steps to find the absolute minimum of $f(x) = x^2 + 4x + 4$ within the interval, $[-4, 4]$. Since $f(x)$ is a quadratic function, the function is continuous throughout its domain.

Differentiate $f(x)$ then equate the expression to zero.

\begin{aligned}f(x) &= x^2 + 4x + 4\\f^{\prime}(x)&=\dfrac{d}{dx}(x^2 + 4x + 4)\\&=\dfrac{d}{dx}x^2 + \dfrac{d}{dx}4x + \dfrac{d}{dx}4,\phantom{x}{\color{DarkOrange}\text{Sum Rule}}\\&=\dfrac{d}{dx}x^2 + {\color{DarkOrange}4\dfrac{d}{dx}x} + {\color{DarkOrange}0},\phantom{x}{\color{DarkOrange}\text{Constant Multiple & Constant Rules}} \\&={\color{DarkOrange}2x}+ 4({\color{DarkOrange}1}),\phantom{x}{\color{DarkOrange}\text{Power Rule}}\\&= 2x + 4 \end{aligned}

Find the values of $x$ that satisfy the quadratic equation.

\begin{aligned}f^{\prime}(x)&=0\\2x + 4 &= 0\\2x &= -4\\x&= -2\end{aligned}

The critical number, $x = -2$, is within the given interval. Let’s find the values of $f(x)$ at $x= -4$, $x= -2$, and $x= 4$.

Since $f(x)$ is at its lowest when $x = -2$ for the interval, $[-4, 4]$, $\boldsymbol{f(x)}$ has an absolute minimum of $0$.

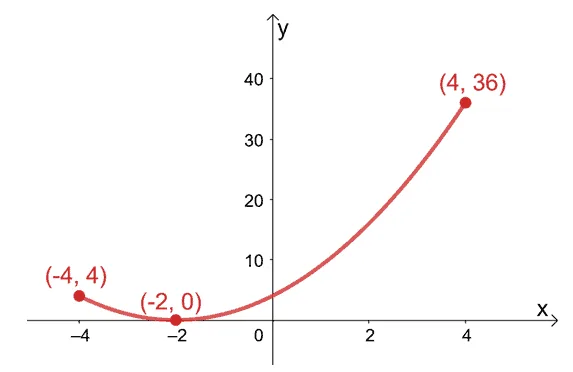
Here’s the graph of $f(x) = x^2 + 4x + 4$ within the interval, $[-4, 4]$. This graph confirms that it has a minimum point at $(-2, 0)$ and consequently, an absolute minimum of $0$.

We’ll try out more examples to master our knowledge on the absolute minimum. Apply a similar approach when solving the problems shown below!

Example 1

Graph $f(x) = x^2 – 6x + 9$’s curve throughout the interval, $[-4, 10]$. Using its graph, what is $f(x)$’s absolute minimum?

Solution

Find four points of $f(x)$ within the interval, $[-4, 10]$.

Connect these points to graph $f(x)$. Find the lowest point of the graph using its curve.

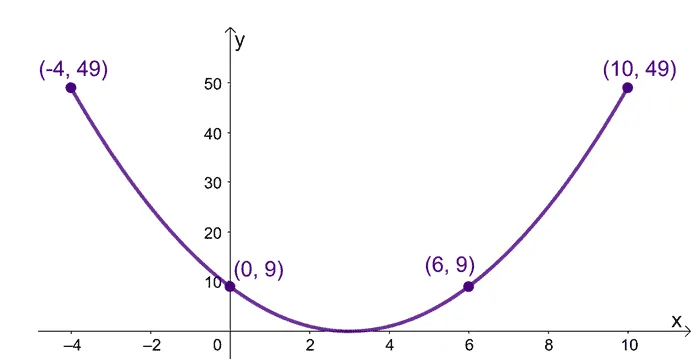
We can see that $f(x)$’s lowest point is $(-3, 0)$, so $f(x)$ has an absolute minimum of $\boldsymbol{0}$. This example confirms the fact that we can find the function’s absolute minimum by inspecting its graph’s lowest point.

Example 2

Determine the absolute maximum of the function $g(x) = 6x + \dfrac{6}{x}$ over the interval, $[0.5, 2.5]$, if it exists.

Solution

The function $g(x)$ is continuous within the interval, $[0.5, 2.5]$, so we can proceed by differentiating $g(x)$ first.

\begin{aligned}g(x) &= 6x + \dfrac{6}{x}\\&=6\left(x + \dfrac{1}{x} \right )\\\\g^{\prime}(x)&=\dfrac{d}{dx} \left[6\left(x + \dfrac{1}{x} \right )\right]\\&= 6\dfrac{d}{dx} \left(x + \dfrac{1}{x} \right ), \phantom{x}\color{DarkOrange}\text{Constant Multiple Rule}\\&= 6{\color{DarkOrange}\left(\dfrac{d}{dx} x + \dfrac{d}{dx} \dfrac{1}{x} \right )}, \phantom{x}\color{DarkOrange}\text{Sum Rule}\\&= 6\left(\dfrac{d}{dx} x + \dfrac{d}{dx} x^{-1}\right)\\&= 6({\color{DarkOrange}1 -1x^{-2} }),\phantom{x}\color{DarkOrange}\text{Power Rule}\\&=6 -\dfrac{6}{x^2}\end{aligned}

Find the critical numbers of $g(x)$ by solving the equation, $g^{\prime}(x) =0$.

\begin{aligned}g^{\prime}(x)&=0\\6 -\dfrac{6}{x^2}&=0\\6x^2 -6&= 0\\x^2&= 1\\x &= \pm1\end{aligned}

Only account for critical numbers within the given interval, so we only have $x =1$ for $g(x)$. Now, let’s observe the values of $g(x)$ at $x = 0.5$, $x= 1$, and $x =2.5$.

From the table of values, we can see that the lowest value of $g(x)$ is $12$, so $g(x)$ has an absolute minimum of $12$ within the interval, $[0.5, 2.5]$.

Example 3

James is planning to construct a rectangular enclosure with an area of $800$ $\text{ft}^2$.  He is planning to use wood for the three sides and the material would cost $\$8$ per foot.  James plans to construct the fourth side using cement and that costs $\$16$ per foot.  What should the dimensions be to minimize the cost?  What is the minimum cost?

Solution

Since the rectangular enclosure has an area of $800\text{ ft}^2$. Let’s say the rectangular enclosure is $x$ feet wide, then it is $\dfrac{800}{x}$ feet long.

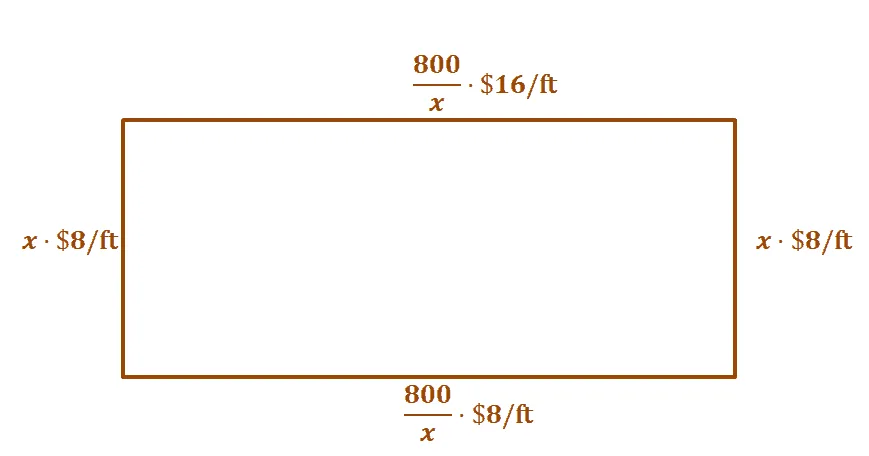
The total cost, $C(x)$, can be expressed by adding the total cost of materials for all four sides.

\begin{aligned}C(x) &= 8\left[2 (8x) + \dfrac{800}{x}(16 + 8)\right]\\&= 8\left(16x + \dfrac{19200}{x}\right)\end{aligned}

To find the global minimum of $C(x)$, let’s find $C^{\prime}(x)$.

\begin{aligned}C(x)&= 8\left(16x + \dfrac{19200}{x}\right)\\&= 108x + \dfrac{153600}{x}\\C^{\prime}(x) &=  \dfrac{d}{dx}\left(108x + \dfrac{153600}{x} \right )\\&= \dfrac{d}{dx}108x + \dfrac{d}{dx}\dfrac{153600}{x},\phantom{x}{\color{DarkOrange}\text{Sum Rule}} \\&={\color{DarkOrange}108} \dfrac{d}{dx}x + {\color{DarkOrange}153600}\dfrac{d}{dx}\dfrac{1}{x},\phantom{x}{\color{DarkOrange}\text{Constant Multiple Rule}}\\&=108 ({\color{DarkOrange}1}) + 153600({\color{DarkOrange}-x^2}),\phantom{x}{\color{DarkOrange}\text{Power Rule}}\\&= 108 – \dfrac{153600}{x^2}\end{aligned}

Equate $C^{\prime}(x)$ to zero then find the values of $x$ that satisfy the equation.

\begin{aligned}C^{\prime}(x) &=0 \\108 – \dfrac{153600}{x^2}&= 0\\108x^2 – 153600 &=0 \\x^2 &= \dfrac{153600}{108}\\x&= \pm \dfrac{80\sqrt{2}}{3}\\&\approx 37.71\end{aligned}

We’ll only choose $x = 37.71\text{ ft} $ since $x$ represents the enclosure’s width. Since the enclosure’s area is $800\text{ ft}^2$, $x$ must be within $[1, 800]$. Let’s observe the values of $x$ given the endpoints of the interval and critical number of $C(x)$.

This means that $C(x)$ has a global minimum of $8900.12$ dollars when $x \approx 37.12\text{ ft}$. This value makes sense since the endpoints will be higher as $C(x)$ is increasing throughout the interval.

This means that the dimensions of the rectangular enclosure are $\boldsymbol{37.12\text{ ft}}$ and $\dfrac{800}{37.12} \approx \boldsymbol{21.55\text{ ft}}$. The minimum cost would be $\boldsymbol{\$ 8900.12}$.

Practice Questions

1. Graph $f(x) = x^2 – 8x + 16$’s curve throughout the interval, $[-4, 12]$. Using its graph, what is $f(x)$’s absolute minimum?

2. Determine the absolute minimum of the function $g(x) = 12x + \dfrac{12}{x}$ over the interval, $[-4, 4]$, if it exists.

3. Determine the absolute minimum of the function $h(x) = xe^{3x}$ over throughout its domain.

4. Jennifer realized that the amount she saved in a particular bank account after $x$ years is given by, $A(x) = 5000 – 10xe^{6 – \dfrac{x^2}{6}}$. Using this model, determine the minimum amount that was in Jennifer’s account during the first $10$ years?

Answer Key

1. Global minimum at $0$

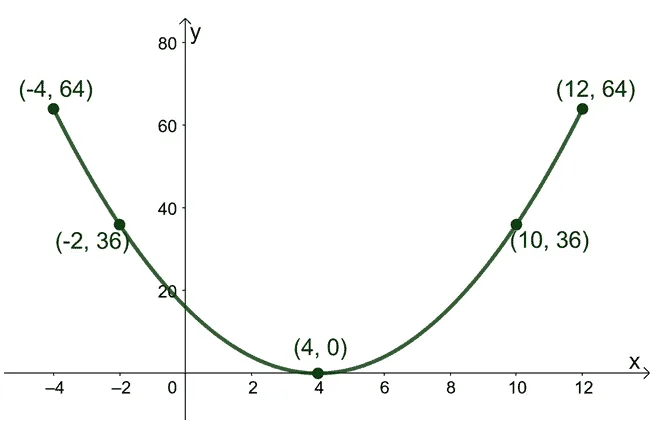
2. $24$
3. $-\dfrac{1}{3e} \approx -0.123$
4. $A = 5000 – 10 \sqrt{3}e^{\frac{11}{2}} \approx 761.81$ dollars

Images/mathematical drawings are created with GeoGebra.