Absolute Value – Properties & Examples

What is an Absolute Value?

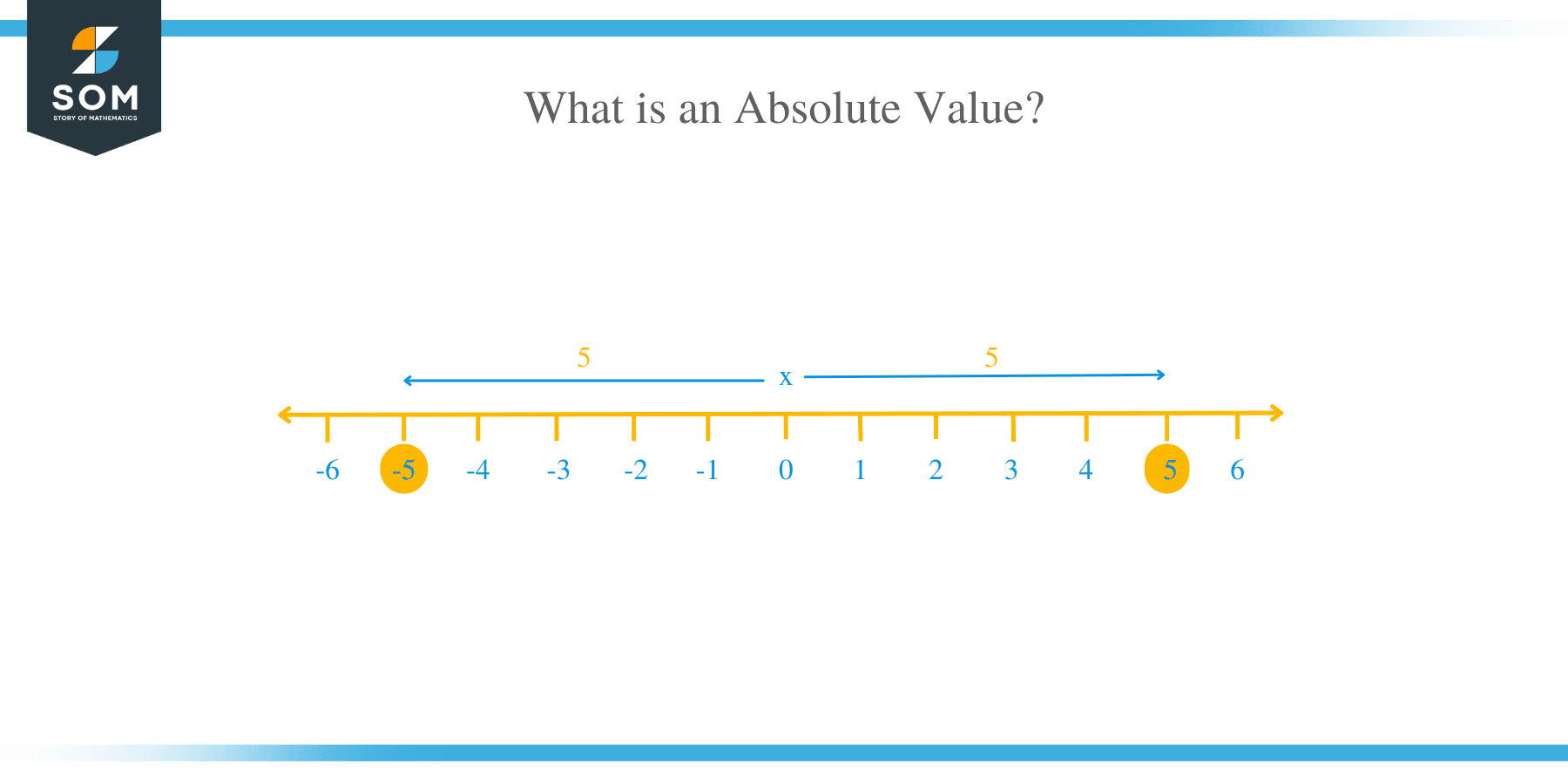
Absolute value refers to a point’s distance from zero or origin on the number line, regardless of the direction. The absolute value of a number is always positive.

The absolute value of a number is denoted by two vertical lines enclosing the number or expression. For example, the absolute value of the number 5 is written as, |5| = 5. This means that distance from 0 is 5 units:

Similarly, the absolute value of a negative 5 is denoted as, |-5| = 5. This means that distance from 0 is 5 units:

Not only does a number show the distance from the origin, but it also is important for graphing the absolute value.

Consider an expression |x| > 5. To represent this, on a number line, you need all numbers whose absolute value is greater than 5. This is done graphically by placing an open dot on the number line.

Consider another case where |x| = 5. This includes all absolute values that are less than or equal to 5. This expression is graphed by placing a closed dot on the number line. The equal sign indicates that all values being compared are included in the graph.

An easy way of representing expression with inequalities is by following the following rules.

• For |x| < 5, -5 < x < 5
• For |x| = 5, -5 = x = 5
• For |x + 6| < 5, -5 < x + 6 < 5

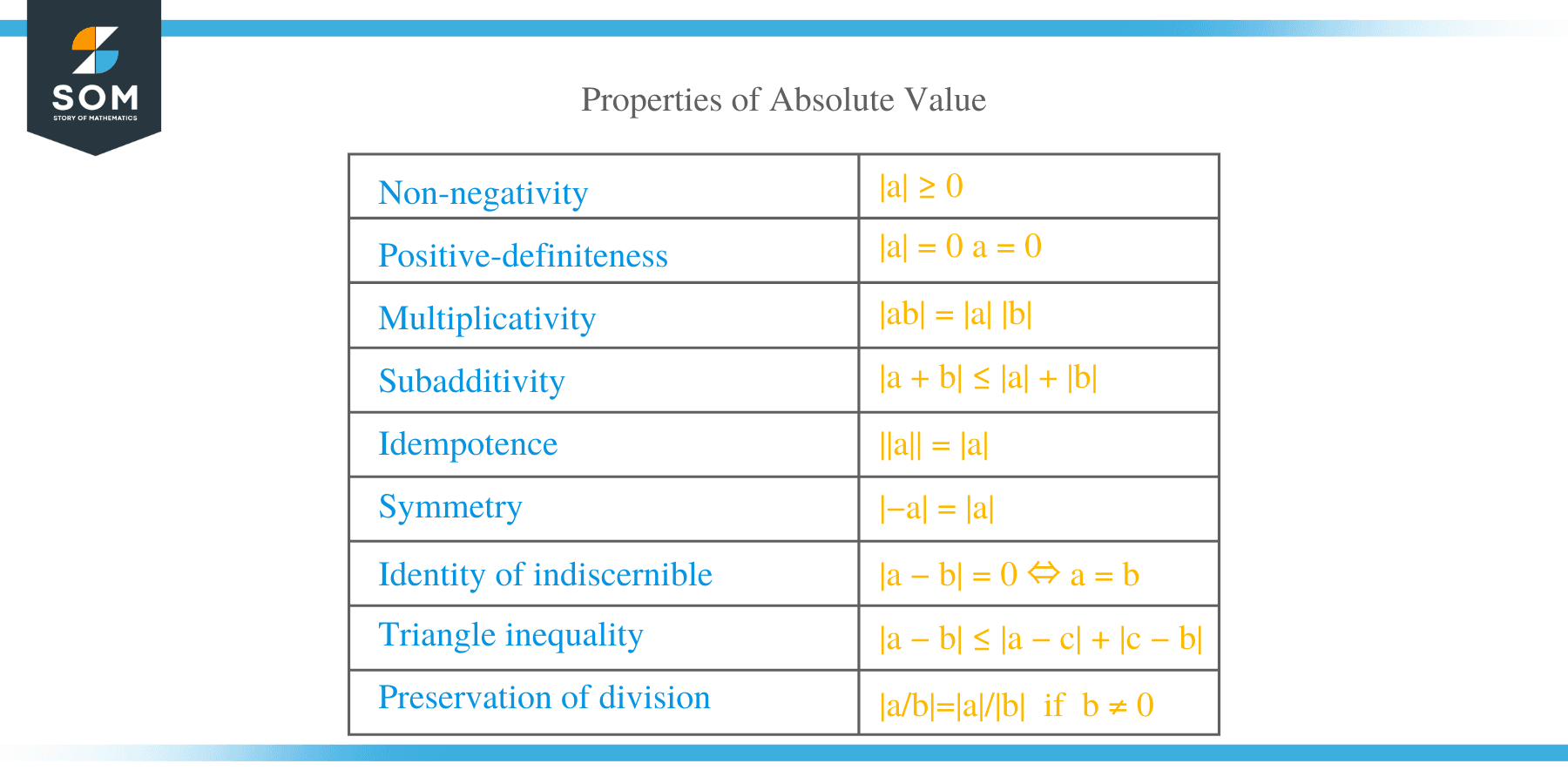
Properties of Absolute Value

Absolute value has the following fundamental properties:

1. Non-negativity |a| ≥ 0
2. Positive-definiteness |a| = 0a = 0
3. Multiplicativity         |ab| = |a| |b|
4. Subadditivity |a + b| ≤ |a| + |b|
5. Idempotence ||a|| = |a|
6. Symmetry |−a| = |a|
7. Identity of indiscernible |a − b| = 0 ⇔ a = b
8. Triangle inequality |a − b| ≤ |a − c| + |c − b|
9. Preservation of division |a/b|=|a|/|b|  if  b ≠ 0

Example 1

Simplify -|-6|

Solution

• Convert the absolute value symbols to parentheses

–| –6 | = – (6)

• Now I can take the negative through the parentheses:

– (6) = – 6

Example 2

Find the possible values of x.

|4x| = 16

Solution

In this equation, 4x can be either positive or negative. So, we can write it as:

4x = 16                        or                     -4x = 16

Divide both sides by 4.

x = 4                or                     x = -4

Hence, the two possible values of x are -4 and 4.

Example 3

Solve the following problems:

a)        Solve | –9|

Answer

| –9| = 9

b)        Simplify | 0 – 8 |.

Answer

| 0 – 8 | = | –8 | = 8

c)        Solve | 9 – 3 |.

Answer

| 9 – 3 | = | 6| = 6

d)        Simplify | 3 – 7 |.

Answer

| 3 – 7 | = | –4 | = 4

e)        Workout | 0 (–12) |.

Answer

| 0(–12) | = | 0 | = 0

f)         Simplify | 6 + 2(–2) |.

Answer

| 6 + 2(–2) | = | 6 – 4 | = | 2| = 2

g)        Solve –| –6 |.

Answer

–| –6| = – (6) = –6

h)        Simplify –| (–7)² |.

Answer

–| (–7)² | = –| 49 | = –49

i)         Calculate –| –9 |²

Answer

–| –9 |² = – (9) ² = –(4) = –81

j)         Simplify (–| –3|) ².

Answer

(–| –3|)² = (–(3)) ² = (–3) ² = 9

Example 4

Evaluate: -|-7 + 4|

Solution

• First of all, start by working out the expressions within the absolute value symbols:
  -|-7 + 4| = -|-3|
• Introduce parentheses
  -|-3| = -(3) = -3
• So, the answer is -3.

Example 5

A sea diver is -20 feet below the surface of the water. How far does he need to swim to get to the surface?

Solution

He needs to swim |-20| = 20 feet.

Example 6

Calculate the absolute value of 19 – 36(3) + 2(4 – 87)?

Solution

19 – 36 (3) + 2 (4 – 87)

= 19 – 108 + 2 (-83)

= 19 – 108 – 166

= -255

Example 7

Solve the equation by determining absolute values,

2 |-2 × – 2| – 3 = 13

Solution

Rewrite the expression with the absolute value sign on one side.

• Add 3 to both sides of the expression

2 | – 2 × – 2| – 3 + 3 = 13 + 3

2 | – 2 × – 2| = 16

• Divide both sides by 2.

|- 2 × – 2| = 8

• The remaining equation is same as to writing the expression as:

– 2 × – 2 = 8 or – 8

1. a) -2 x – 2 = 8

Now solve for x
x = – 5

1. b) – 2 x – 2 = – 8

x = 3

• The correct answer is (-5, 3).

Example 8

Calculate the real values to the expression with absolute value.

|x – 1| = 2x + 1

Solution

One method of solving this equation is to consider two cases:
a) Assume x – 1 ≥ 0 and rewrite the expression as:

x – 1 = 2x + 1

Calculate the value of x
x = -2
b) Assume x – 1 ≤ 0 and rewrite this expression as
-(x – 1) = 2x + 1
– x + 1 = 2x + 1
find x as
x = 0

It is important to check if the solutions are correct for the equation because all the values of x were assumed.
Substituting x by – 2 in both sides of the expression gives.

| (-2) – 1| = |-2 + 1| = 1 to the left-hand side and 2(-2) + 1 = – 3 to the right side

Since the two equations are not equal, therefore x = -2 is not an answer to this equation.
Check for x = 0

Substituting x by 0 in both sides of the equation results in:

|(0) – 1| = 1 to the left side and 2(0) + 1 = 1 to the right.

The two expressions are equal and therefore, x = 0 is the solution to this equation.