Adding and Subtracting Integers – Methods & Examples

Integers are whole numbers used in counting, inclusive of negative, positive and zero numbers. The concept of integers was first started in the ancient Babylon and Egypt.

Integers can be represented on a numbers line, with the positive integers occupying the right side of zero and negative integers occupying the left side of zero. In Mathematics, integers are usually represented by ‘Zahlen’ symbol i.e. Z = {…, -4, -3, -2, -1,0,1,2,3, 4…}.

Arithmetic operations such as addition, subtraction, multiplication and division are applicable to integers. Addition and subtraction of integers helps to determine the sum or total and difference of the integers. Similarly, multiplication and division are used to compare and divide integers into equal parts. In this article, our focus is how to perform addition and subtraction with integers.

Integers are a special group of numbers that are positive, negative and zero, which are not fractions. Rules for addition and subtraction are the same for all, whether it is a natural number or an integer because natural numbers are itself integers

How to Add Integers?

There are three possibilities when adding integers. They are:

• Addition between two positive integers
• Addition of two negative integers
• Addition between a positive and a negative integer.

The addition of two positive integers result in a positive answer. For example, +4 + (+3) = +7. Positive integers are never written with a positive sign and for this case, the answer is just 7.

When a positive and a negative integer are added, the numbers are subtracted without signs and the answer is assigned the sign of the larger integer. For example, to add 10 + (-15) = -5, the larger number in this case is 15 without the sign.  Therefore subtract 15 and 10 to get 5 and assign the answer the sign of 15 which is -5.

When adding negative integers, the numbers are added and the sum assumes the sign of the original integers. For example, – 5 + (-1) = – 6.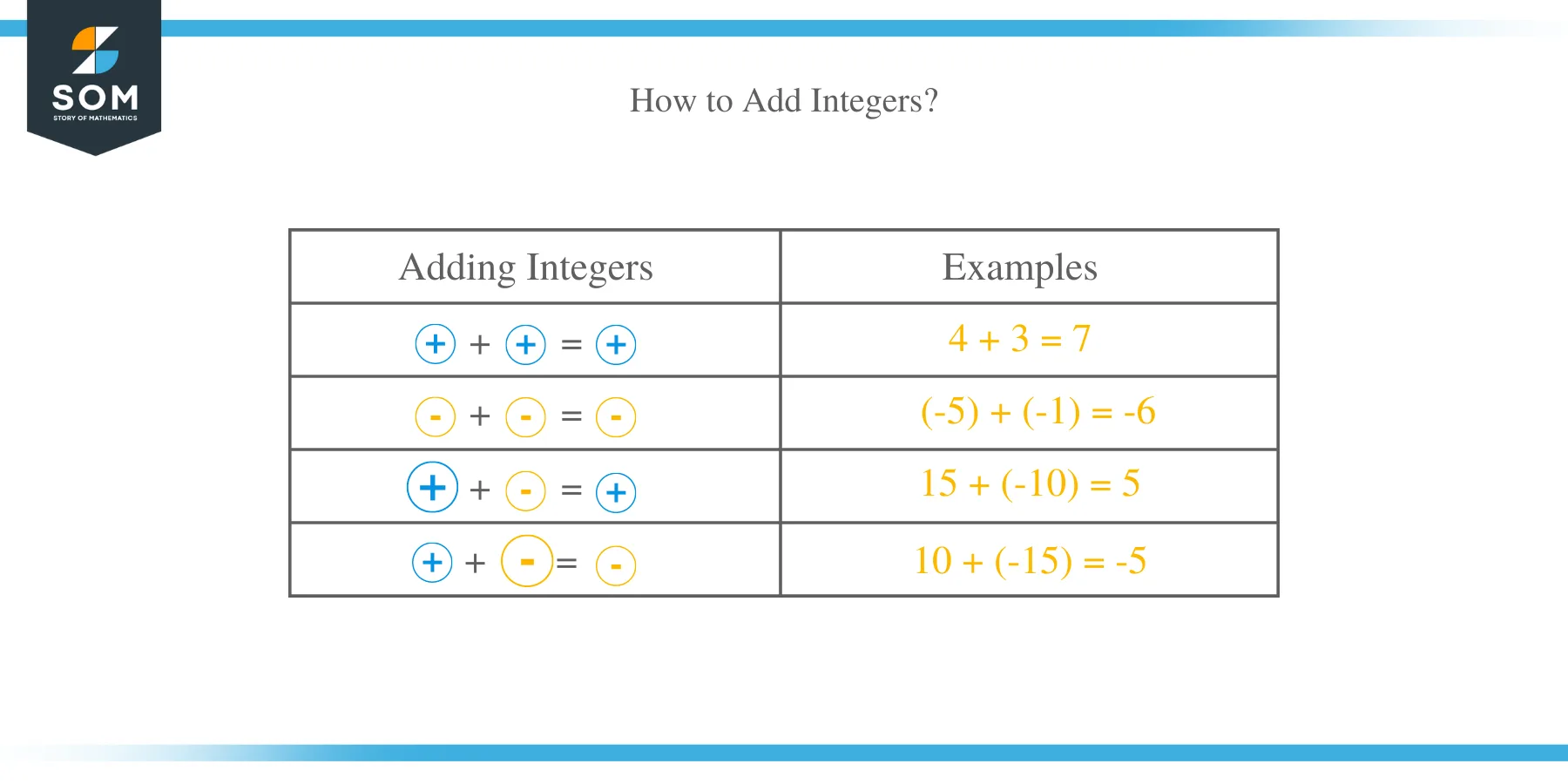

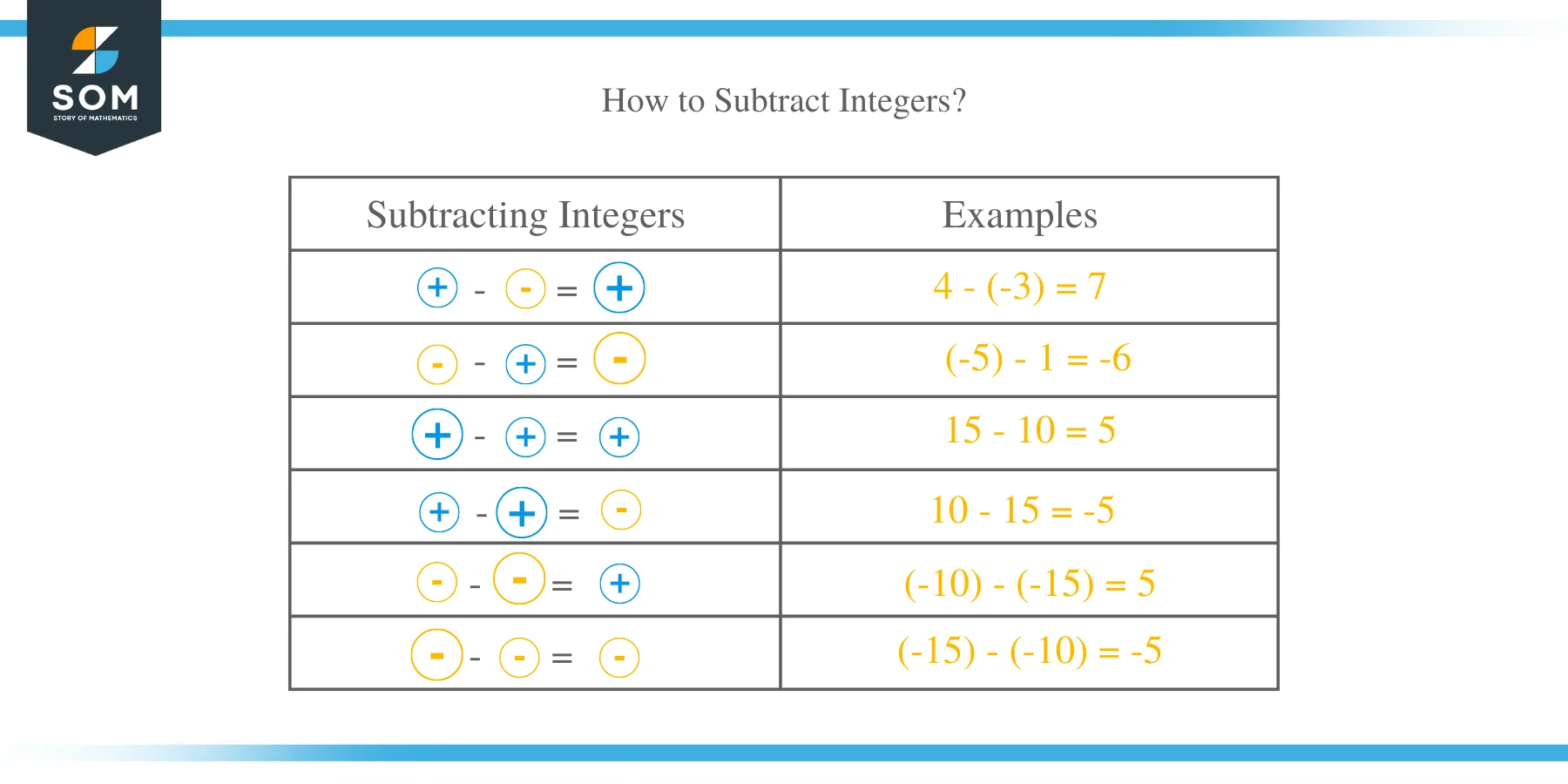
How to Subtract Integers?

Like addition, there are also three possibilities of subtraction of integers:

• Subtraction of two positive integers
• Subtraction of two negative integers
• Subtraction of a positive and a negative integer.

For the ease of subtraction, problems involving subtraction of integers can be modeled into the following transformation:

• The subtraction sign is converted into addition sign
• Take the inverse of the integer that comes after addition the sign.

For example, to subtract (-6) – (8) using the above transformation:

Step 1:

Covert the subtraction sign to an addition sign

⇒ (- 6) + (8)

Step 2:

Take the inverse of the integer that comes after the addition sign. The inverse of 8 is -8.

⇒ –6 + (- 8)

Add the integers and assign the sign of the larger integer

⇒ –6 + (-8) = -14

Example 1

Evaluate:

(-1) – ( -2)

Solution

(-1) – ( -2)

Convert the subtraction sign to addition sign

⇒ (-1) + (-2)

Subtract and put the sign of larger integer

⇒ (-1) + (2)

Hence,

(-1) – ( -2) = 1

Example 2

Add -10 and -19.

Solution

-10 and -19

Since both integers are negative;

Add the integers together and put the sign of the original integers to the result.

(-10) +(-19) = -10-19

= -19

Example 3

Subtract -10 – (-19).

Solution

(-10) – (-19)

In this case the two negative signs will become positives, so;

-10 + 19 = 19 -10

= 9

Example 4

Evaluate 9 – 10 +(-5) + 6

Solution

Begin by opening the brackets.

= 9 – 10 -5 + 6

Separately, add the positive and negative integers.

= (9 + 6) – 10 -5

= 15 – 15

= 0