Adding Exponents – Techniques & Examples

Algebra is one of the core courses in mathematics. To understand algebra, it is fundamental to know how to use exponents and radicals.  Addition of exponents forms part of the algebra syllabus, and for this reason, it essential for students to have a stronger foundation in mathematics.

Many students often confuse addition of exponents with addition of numbers, and hence they end up making mistakes. These confusions usually entail the difference in meaning of terms such as exponentiation and exponents.

Before diving into tips on how to add exponents, lets start by defining terms on exponents.  To start with, an exponent, is simply the repeated multiplication of a number by itself. In mathematics, this operation is referred as exponentiation. Exponentiation is therefore an operation involving numbers in the form of b ⁿ, where b is referred to as the base and the number n is the exponent or index or power.  For example, x⁴ contain 4 as an exponent, and x called the base.

Exponents are sometimes called powers of a numbers. An exponent represents the number of times a number is to be multiplied by itself.  For instance, x⁴ = x × x × x × x.

How to Add Exponents?

To add exponents, both the exponents and variables should be alike. You add the coefficients of the variables leaving the exponents unchanged. Only terms that have same variables and powers are added. This rule agrees with the multiplication and division of exponents as well.

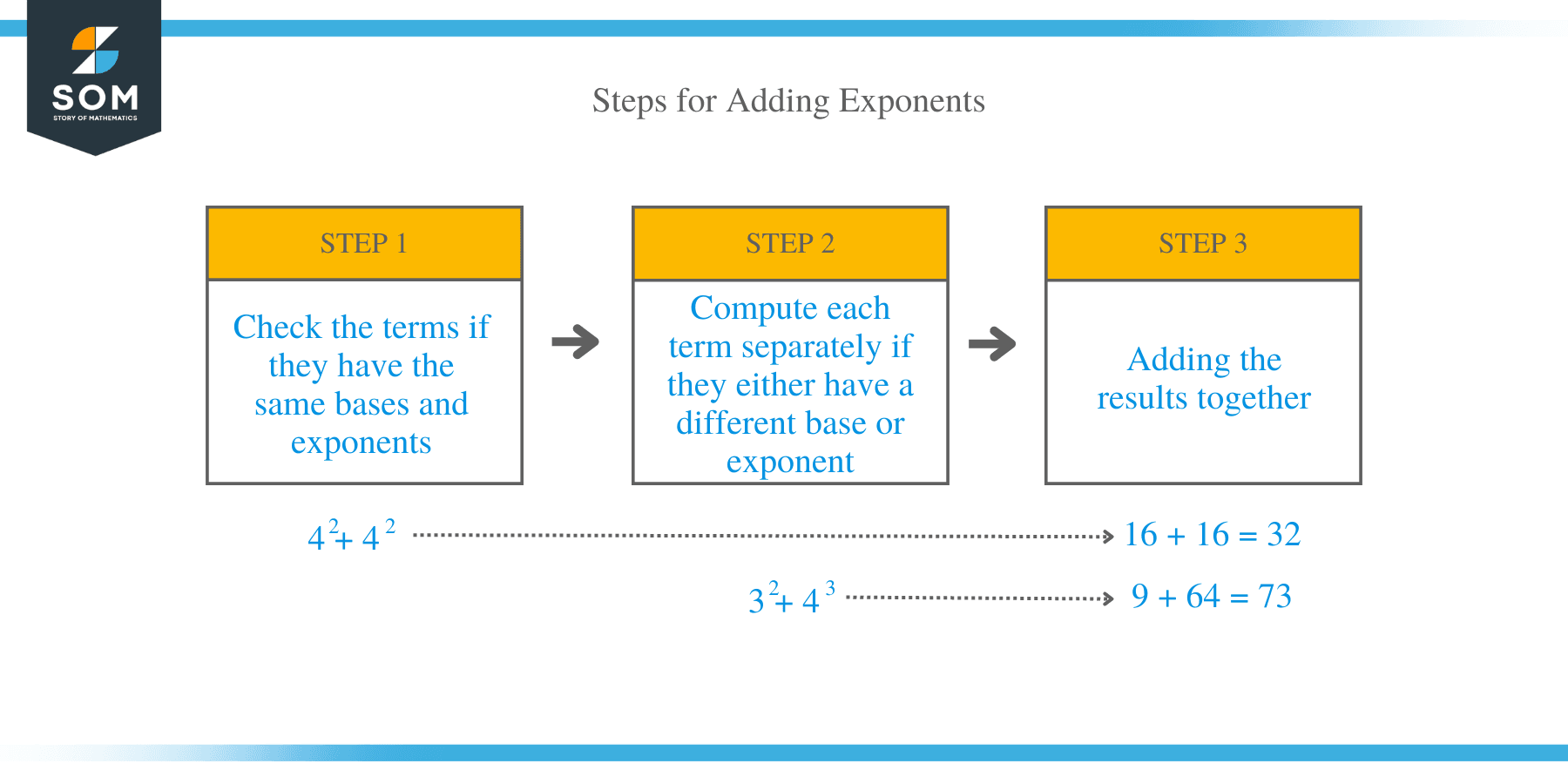
Below are the steps for adding exponents:

• Check the terms if they have the same bases and exponents

For example, 4²+4², these terms have both the same base 4 and exponent 2.

• Compute each term separately if they either have a different base or exponent

For example, 3² + 4³, these terms have both different exponents and bases.

• Add the results together.

Adding exponents with different exponents and bases

Adding exponents is done by calculating each exponent first and then adding: The general form such exponents is: a ⁿ + b ^m.

Example 1

1. 4²+ 2⁵= 4⋅4+2⋅2⋅2⋅2⋅2 = 16+32 = 48
2. 8³+ 9²= (8)(8)(8) + (9)(9) = 512 + 81 = 593
3. 3²+ 5³= (3)(3) + (5)(5)(5) = 9 + 125 = 134
4. 6²+ 6³= 252.
5. 3⁴+ 3⁶= 81 + 729 = 810.

Adding exponents with same bases and exponents

The general formula is given by:

bⁿ + b ⁿ = 2b ⁿ

Example 2

1. 4²+ 4²= 2⋅4² = 2⋅4⋅4 = 32
2. 8³+ 8³+ 8³ = 3(8³) = 3 * 512 = 1536
3. 3²+ 3²= 2(3²) = 2 * 9 = 18
4. 5²+ 5²= 2(5²) = 2 * 25 = 50.

How to add negative exponents with different bases?

Adding negative exponents is done by computing each exponent separately and then adding:

a^-n + b^-m = 1/aⁿ + 1/b ^m

Example 3

4^-2 + 2^-5 = 1/4² + 1/2⁵ = 1/(4⋅4)+1/(2⋅2⋅2⋅2⋅2) = 1/16+1/32 = 0.09375

How to add fractional with different bases and exponents?

Adding fractional exponents is done by calculating each exponent separately and then adding:

a^n/m + b ^k/j.

Example 4

3^3/2 + 2^5/2 = √ (3³) + √ (2⁵) = √ (27) + √ (32) = 5.196 + 5.657 = 10.853

How to add fractional exponents with same bases and same fractional exponents?

b^n/m + b ^n/m = 2b^n/m

Example 5

4^2/3 + 4^2/3 = 2⋅4^2/3 = 2 ⋅ ³√ (4²) = 5.04

How to add variables with different exponents?

Adding exponents is done by computing each exponent separately and then adding:

xⁿ + x ^m

How to add variables with same exponents?

xⁿ + x ⁿ = 2xⁿ

Example 6

x² + x² = 2x²

Example 7

(4^-1 + 8^-1) ÷ (2/3)^-1

= (1/4 + 1/8) ÷ (3/2)

= (2 + 1)/8 ÷ 3/2

= (3/8 ÷ 3/2)

= (3/8 ÷ 2/3)

= ¼

Example 8

Simplify: (1/2)^-2 + (1/3)^-2 + (1/4)^-2
Solution:
(1/2)^-2 + (1/3)^-2 + (1/4)^-2
= (2/1)² + (3/1)² + (4/1)²
= (2² + 3² + 4²)
= (4 + 9 + 16)
= 29