- Home
- >
- Adding Fractions – Methods & Examples
JUMP TO TOPIC
Adding Fractions – Methods & Examples
 How to Add Fractions?
How to Add Fractions?
To add the two fractions, the denominators of both fractions must be the same. Let’s take help of the following example to solve a simple fraction problem.
Example 1
1/2 + 1/2
We start by getting the L.C.M of the denominator which will be easy since the L.C.M of two numbers that are the same is that number.
Therefore our L.C.M. is 2
1/2+1/2 = /2
We divide the L.C.M. by the first denominator and then multiply the answer with the first numerator (This will become important when we get to addition of numbers with different denominators).
2 ÷ 2 = 1
1 × 1 = 1
We divide the L.C.M. by the second denominator and then multiply the answer with the second numerator.
2 ÷ 2 = 1
1 × 1 = 1
We then add the two results we have gotten above the L.C.M
1/2 + 1/2 = (1 + 1)/2
= 2/2
To get the answer in simplest form we will divide both the numerator and denominator by
2 to get:
1/1 = 1
Example 2
1/3+1/3
We start by getting the L.C.M of the denominator which will be easy since the L.C.M of two numbers that are the same is that number.
Therefore our L.C.M. is 3
1/3+1/3= /3
We divide the L.C.M. by the first denominator and then multiply the answer with the first numerator.
3÷3=1
1×1=1
We divide the L.C.M. by the second denominator and then multiply the answer with the second numerator.
3÷3=1
1×1=1
We then add the two results we have gotten above the L.C.M
= (1+1)/3
=2/3
Addition of fractions having different numerators and same denominator
To understand this case, let’s see step by step solutions of the examples below.
Example 3
2/6+3/6
The L.C.M is 6 since the two denominators are the same
2/6+3/6= /6
The L.C.M which is 6 divided by the first denominator is 1, multiply 1 by the first numerator is =2
6 divided by the second denominator is 1, multiply by the second numerator is
=3
=2/6+3/6= (2+3) /6
We add the numerators above the L.C.M.
=5/6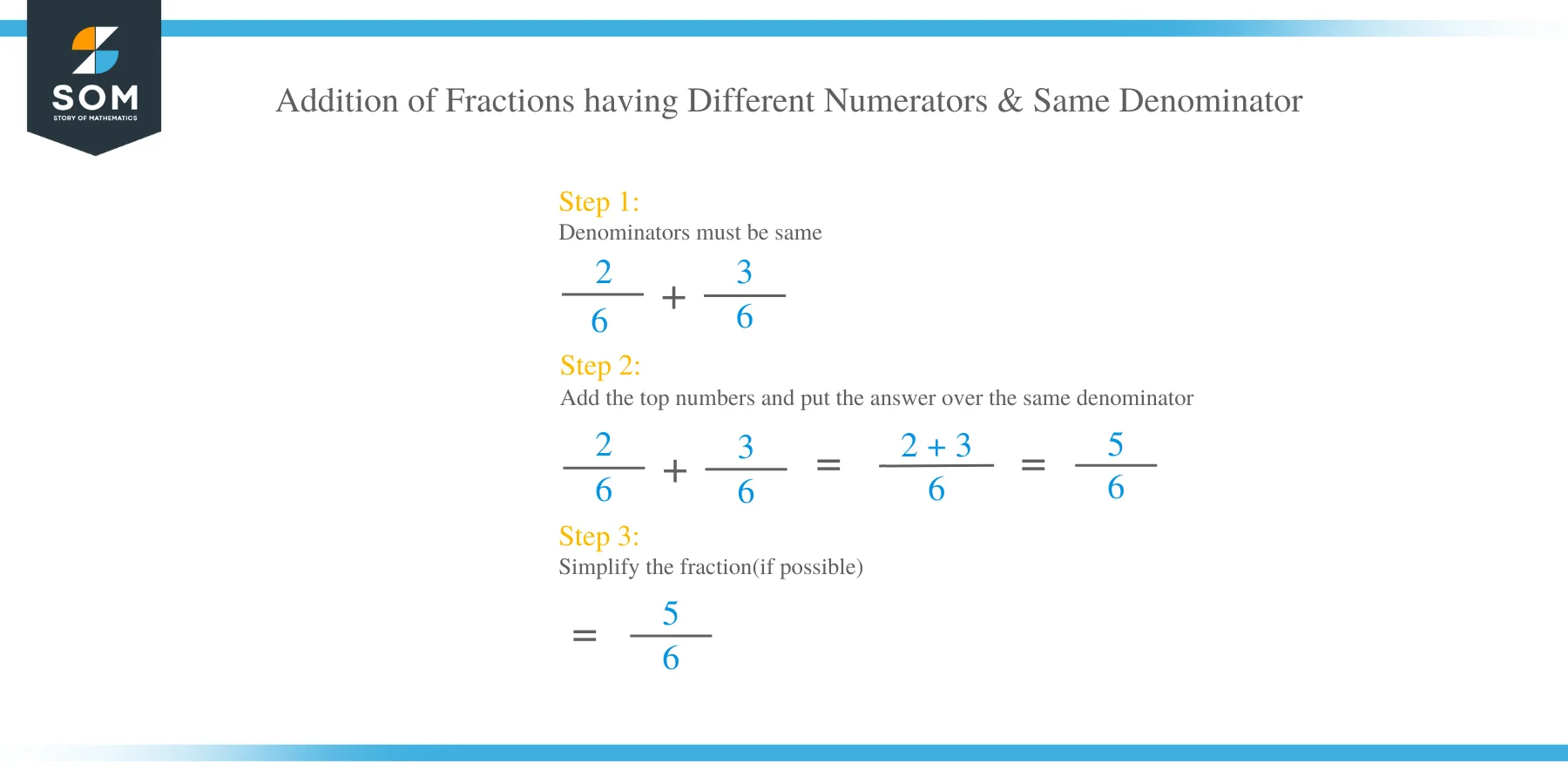
Example 4
The L.C.M is 4 since the two denominators are the same
1/4+2/4= /4
The L.C.M which is 4 divided by the first denominator which is 4 is 1, multiply 1 by the first numerator which is 1 to get =1
4 divided by the second denominator which is 4 is 1, multiply 1 by the second numerator which is 2 to get 2
We add the numerators above the L.C.M. as follows
1/4+2/4
= (1+2)/4
=3/4
Addition of fractions having different numerators and different denominator
To understand this case, let’s see step by step solutions of the examples below.
Example 5
We find the L.C.M. of 4 and 6
| 2 | 4 | 6 |
| 2 | 2 | 3 |
| 3 | 1 | 3 |
| 1 | 1 |
The L.C.M. is 2×2×3=12
=3/4+1/6= /12
Divide the L.C.M. which is 12 by the first denominator 4=3
Multiply 3 by the first numerator 3=9
Divide the L.C.M. which is 12 by the second denominator 6=2
Multiply 2 by the second numerator 1 =2
Then add the 9+2 above the L.C.M.
=3/4+1/6= (2+9) /12
=11/12
Example 6
5/7+1/3
We start by getting the L.C.M. of the two denominators 7 and 3
| 3 | 7 | 3 |
| 7 | 7 | 1 |
| 1 | 1 |
The L.C.M. is 21
Divide the L.C.M. which is 21 by the first denominator which is 7 to get =3
Multiply 3 by the first numerator which is 3 to get=9
Divide the L.C.M. which is 21 by the second denominator which is 6 to get=2
Multiply 2 by the second numerator which is 1 to get =2
Then add the two results 9 and 2 above the L.C.M. to get the following
=5/7+1/3= (15+7)/21
=22/21
