Adding Mixed Numbers – Methods & Examples

How to Add Mixed Fractions?

In this article, we are going to learn on how to add of mixed fractions or mixed numbers. There are two methods to add the mixed fractions.

Method 1

In this method, whole numbers separately added. The fractional parts are also added separately. If the fractions have different denominators, then find their L.C.M. and change the fractions into like fractions. The sum of whole numbers and fractions is then calculated.

Example 1

Add: 2 ³/₅ + 1 ³/₁₀

Solution

2 ³/₅ + 1 ³/₁₀ = (2 + 1) + (3/5 + 3/10)

= 3 + (3/5 + 3/10)

The L.C.M. of 5 and 10 = 10

= 3 + (3 × 2/5 × 5 + 3 × 1/10 × 1,

= 3 + 6/10 + 3/10

= 3 + 9/10

= 3 ⁹/₁₀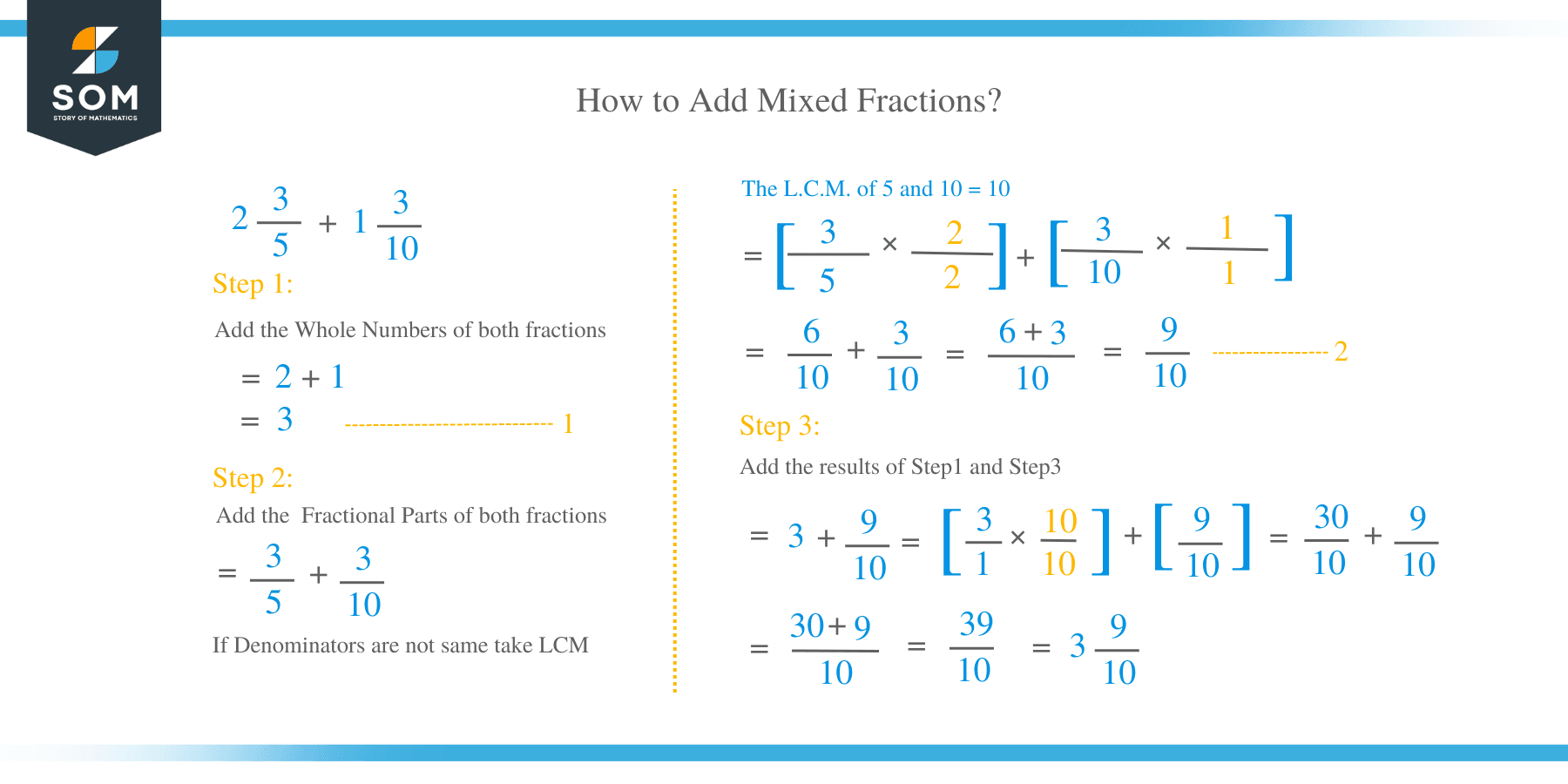

Example 2

Add the following fraction together: 1 ¹/₆, 2 ¹/₈ and 3 ¼

Solution

1 ¹/₆ + 2 ¹/₈ + 3 ¼

= (1 + 2 + 3) + (1/6 + 1/8 + ¼)

= 6 + 1/6 + 1/8 + ¼

L.C.M of 6, 8 and 4 = 24

= 6 + 1 × 4/6 × 4 + 1 × 3/8 × 3 + 1 × 6 /4 × 6

= 6 + 4/24 + 3/24 + 6/24

= 6 + (4 + 3 + 6)/24

= 6 + 13/24

= 6 ¹³/₂₄

Example 3

Add these fractions together: 5 ¹/9, 2 ¹/ ₁₂ and ¾

Solution

5 ¹/9, 2 ¹/ ₁₂ and ¾

= (5 + 2 +0) + (1/9 + 1/12 + ¾)

= 7 + 1/9 + 1/12 + ¾

L.C.M = 36

= 7 + 1 × 4/9 × 4 + 1 × 3/12 × 3 + 3 × 9/4 × 9

= 7 + 4/36 + 3/36 + 27/36

= 7 + (4 + 3 + 27)/36

= 7 + 34/36

= 7 + 17/18,

= 7 ¹⁷/₁₈.

Example 4

Solve:

5/6 + 2 ½ + 3 ¼

Solution

5/6 + 2 ½ + 3 ¼

= (0 + 2 + 3) + (5/6 + ½ + ¼)

= 5 + 5/6 + ½ + ¼

Since the L.C.M =12

= 5 + 5 × 2/6 × 2 + 1 × 6/2 × 6 + 1 × 3/4 × 3

= 5 + 10/12 + 6/12 + 3/12

= 5 + (10 + 6 +3)/12

= 5 + 19/12

The fraction 19/12 can be converted into a mixed fraction.

= 5 + 1⁷/₁₂

= (5 + 1)+ 7/12

= 6 ⁷/12

Method 2

In the second method, the following steps are followed:

• Convert the mixed number into improper fraction.
• Find the L.C.M and convert the fractions into like fractions.
• Find the sum of the fractions and express the final answer in its simplest form.

Add: 2 ³/5 + 1 ³/₁₀

Solution

2 ³/5 = {(5 × 2) + 3}/5=13/5

1 ³/₁₀ = {(1 x 10) + 3} = 13/10

= 13/5 + 13/10

L.C.M = 10

= 13 × 2/5 × 2 + 13 × 1/10 × 1

= 26/10 + 13/10

= 26 + 13/10

= 39/10

= 3 ⁹/₁₀

Example 6

Work out: 2 ³/₉ + 1 ¹/₆ + 2 ²/₃

Solution

2 ³/₉ + 1 ¹/₆ + 2 ²/₃

= {(9 × 2) + 3}/9 + {(6 × 1) + 1}/6 + {(3 × 2) + 2}/3

L.C.M of 9, 6 and 3 is 18, therefore,

= 21/9 + 7/6 + 8/3

= 21 × 2/9 × 2 + 7 × 3/6 × 3 + 8 × 6/3 × 6

= 42/18 + 21/18 + 48/18

= 42 + 21 + 48/18

= 111/18

= 37/6

= 6 ¹/₆

Example 7

Work out: 2 ½ + 3 ¹/₃ + 4 ¼

Solution

2 ½ + 3 ¹/₃ + 4 ¼

= (2 × 2) + 1}/2 + {(3 × 3) + 1}/3 + {(4 × 4) + 1}/4

L.C.M. of 2, 3 and 4 is 12

= 5/2 + 10/3 + 17/4,

= 5 × 6/2 × 6 + 10 × 4/3 × 4 + 17 × 3/4 × 3

= 30/12 + 40/12 + 51/12

= 30 + 40 + 51/12

= 121/12

= 10 ¹/₁₂

How to add mixed numbers with unlike denominators?

Let’s learn this scenario with the help of examples.

Example 8

Work out:

5 ¹/₄ +1¹/₂

Solution

• First, convert the mixed numbers as improper fractions.

5 ¹/₄ = 21/4

1 ¹/₂ = 3/2

• Determine the L.C.M of the denominators

L.C.M = 4

• Rewrite the fractions using the L.C.M

21/4 + 3/2 =21/4 +6/4

=27/4

• 27/4 can be converted into a mixed number as 6 ³/

Example 9

Work out: 2 ³/₉ + 1 ¹/₆ + 2 ²/₃

Solution

2 ³/₉ + 1 ¹/₆ + 2 ²/₃

= {(9 × 2) + 3}/9 + {(6 × 1) + 1}/6 + {(3 × 2) + 2}/3

L.C.M of 9, 6 and 3 is 18, therefore,

= 21/9 + 7/6 + 8/3

= 21 × 2/9 × 2 + 7 × 3/6 × 3 + 8 × 6/3 × 6

= 42/18 + 21/18 + 48/18

= 42 + 21 + 48/18

= 111/18

= 37/6

= 6 ¹/₆