- Home
- >
- Addition – Explanation & Examples
JUMP TO TOPIC
Addition – Explanation & Examples
 Addition is one of the oldest and the most basic arithmetic operation. It is known to mathematicians for more than 6000 years. The ‘counting’ was considered as an early form of addition.
Addition is one of the oldest and the most basic arithmetic operation. It is known to mathematicians for more than 6000 years. The ‘counting’ was considered as an early form of addition.
The first official evidence of addition is that Egyptians and Babylonians used it in 2000 B.C. The symbols of addition and subtraction were invented around the 16th century, but before that, the equations were written in words, making it really time-consuming to solve the problems.
Addition Definition
Generally, addition is defined as combining two or more groups of objects into a single group. Mathematically, addition can be defined as an arithmetic operation in which the sum or total of two or more numbers is determined.
The addition symbol is a plus (+) and is inserted between numbers being added. Performing addition is one of the simplest numerical tasks. Addition is an important skill in all aspects of life, including: at home, school and work.
Parts of Addition
There are 3 parts of addition, the addend, the equal sign, and the sum.
The Addend
In addition, the addends or the summands are numbers or terms being added together. For example, 10 + 6 = 16, 10 and 6 are the addends of this equation.
The Equal Sign
The equal sign indicates that the two halves of the equation are equivalent. For example, in the addition sentence, 10 + 6 = 16, the equal sign is denoted with two short horizontal strokes.
The Sum
The sum in addition sentence is the totals of the addends. For example, in 10 + 6 = 16, the sum is 16.
Understanding the properties of addition is important because it guides you to work with numbers more effectively.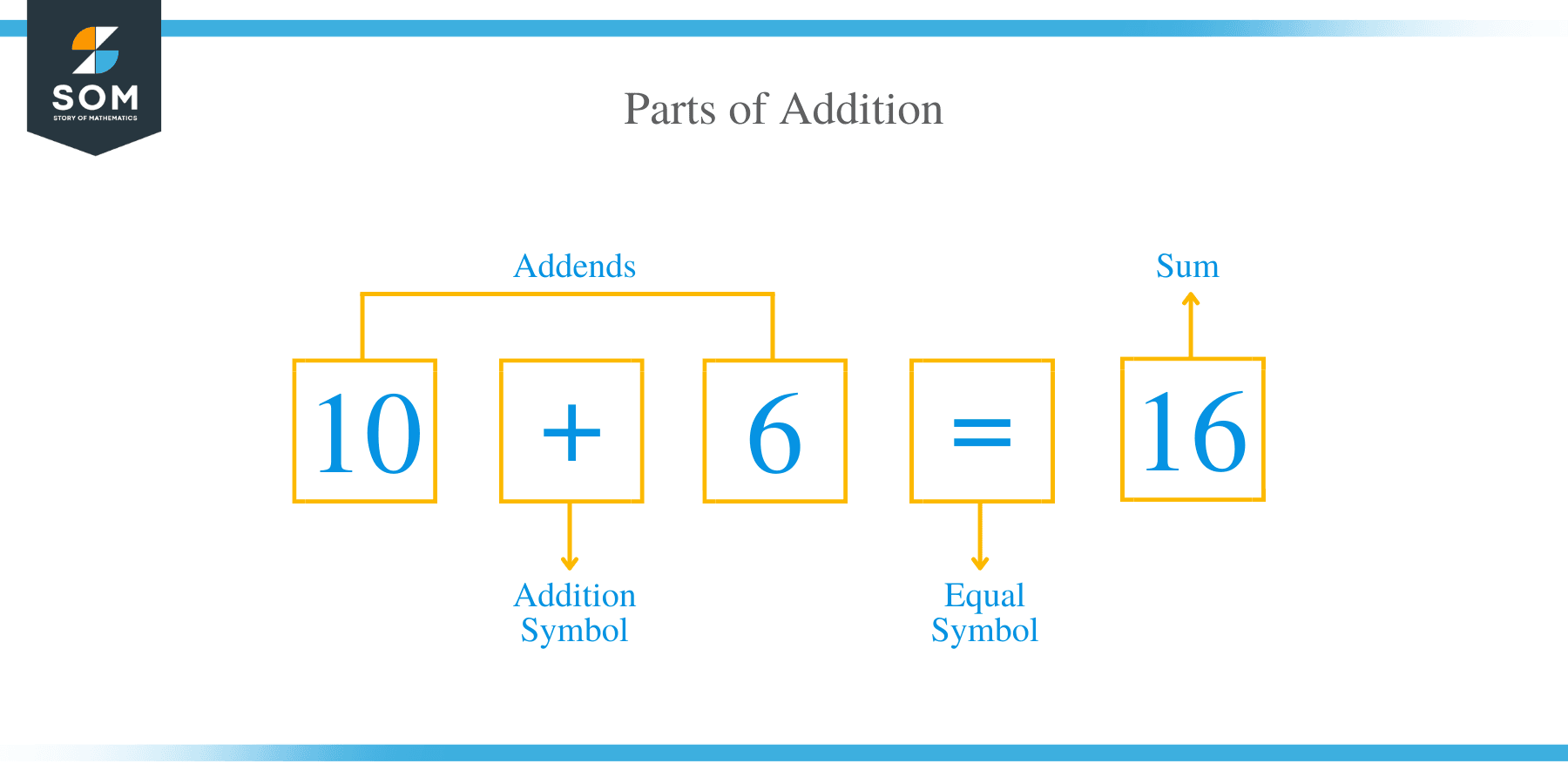
Properties of Addition
- Addition is commutative
This property states that the positions of numbers in an equation do not affect the final answer. For example, 4 + 5 is the same as 5 + 4. This property applies to the addition of numbers, no matter how large the group of numbers is.
- Associative Property
This property applies to complex equations involving brackets, braces, and parenthesis to separate groups of numbers. In addition, we can move the brackets around without affecting the ultimate answer. For example, (4 + 6) + 2 = 4 + (6 + 2).
- Identity Property
The identity property states that the sum of a number with zero is equivalent to the number itself. For example, 5+ 0 = 5. The number zero is called an identity number because it does affect other numbers during the addition.
When a student is adding large groups of numbers, remind them that zero does not affect other numbers in the equation.
- Inverse Operations
The inverse operation implies that the addition and subtraction are opposites. For instance, two plus three minus three is equal to two. Adding and subtracting the same numbers is similar to canceling out the numbers.
For this reason, you should look for numbers that cancel out when performing addition and subtraction on large groups of numbers.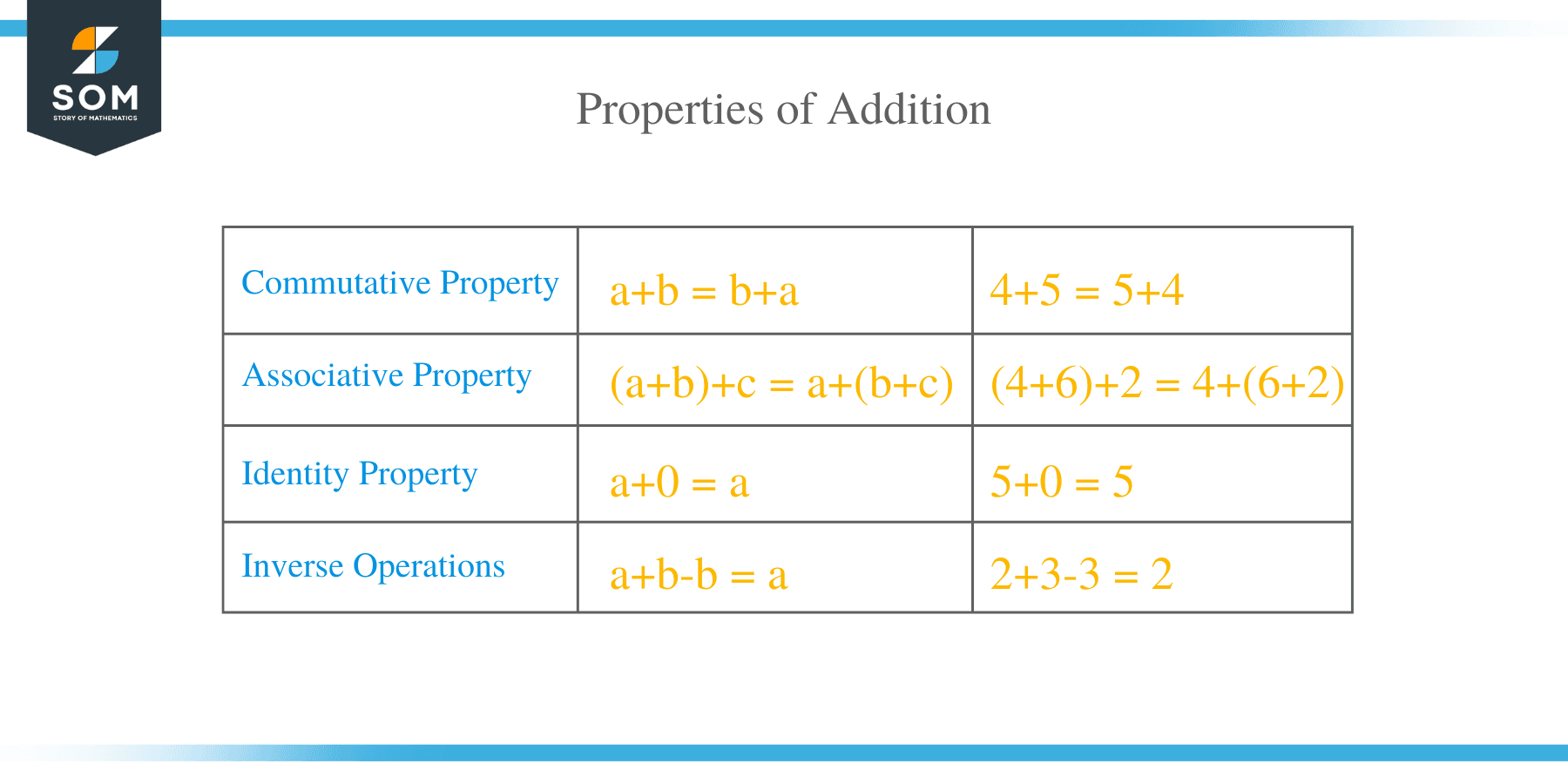
Example 1
Terry bought a designer dress for $231 and shoes for $199. How much money did she spend on the dress and shoes?
Solution
To find the total cost, we need to add 231 and 199
| 2 | 3 | 1 | |
| + | 1 | 9 | 9 |
| 4 | 3 | 0 |
The total expenditure is found by adding the two prices together. Therefore. Terry spent $430 on both items.
Example 2
There are 56 yellow seats and 97 white seats in the school auditorium. How many yellow and white seats are in the auditorium?
Solution
Total number of seats = 56 +97
=153 seats
