Alternate Exterior Angles – Explanation & Examples

In Geometry, there is a special kind of angles known as alternate angles. Alternate angles are non-adjacent and pair angles that lie on the opposite sides of the transversal.

In this article, we are going to discuss alternate exterior angles and their theorem. Before getting into this topic, it is important to recall the following terms: angles, transversal and parallel lines.

For that you need to go through the previous articles on Angles.

What are Alternate Exterior Angles?

Alternate exterior angles are the pair of angles that lie on the outer side of the two parallel lines but on either side of the transversal line.

Illustration:

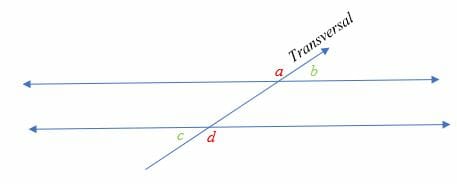
In the diagram above, ∠ a and ∠ d makes a pair of alternate exterior angles and ∠ b and ∠c makes another pair of alternate exterior angles.

Notice how the pairs of alternating exterior angles lie on opposite sides of the transversal but outside the two parallel lines.

Alternating exterior angle theorem

Alternate exterior angle states that, the resulting alternate exterior angles are congruent when two parallel lines are cut by a transversal.

With reference to the diagram above:

• ∠ a = ∠ d
• ∠ b = ∠ c

Proof of alternate exterior angles theorem

Consider the diagram above.

The two lines are parallel.

By vertical angle theorem,

∠ b = 180 – d

By Transitive property of congruence,

∠ b = ∠ c

Similarly, you can prove that,

∠ a = ∠ d

We can also prove the converse of this theorem, according to which if two lines are cut by a transversal, then the alternate exterior angles are congruent.

Let’s solve a few problems on alternate exterior angles.

Example 1

Given that L₁ and L₂ are parallel, find the value of x in the diagram below.

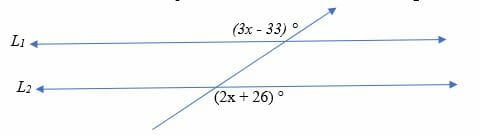
Solution

Angle (2x + 26) ° and (3x – 33) ° are alternate interior angles.  Since L₁ and L₂ are parallel, the two angles are therefore congruent. So, we have;

⇒ (2x + 26) ° = (3x – 33) °

⇒ 2x + 26 = 3x – 33

59 = x

Hence, x = 59 degrees.

Example 2

Two alternating exterior angles are given as (2x + 10) ° and (x + 5) °. Check whether the angles are congruent.

Solution

Alternating exterior angles are equal when the transversal crosses two parallel lines. Therefore, equate the two angles.

⇒ (3x + 10) ° = (x + 50) °

⇒2 x = 40

Divide both sides by 2.

x = 20

Now substitute x in each expression.

⇒ (2x + 10) ° = 50°

(x + 5) = 25°

Hence, (3x + 10) ° ≠ (x + 50) °

The two angles are not congruent. This implies that the two lines intersected by the transversal are not parallel.

Example 3

Prove that alternate exterior angles (2x + 26) ° and (3x – 33) °are congruent.

Solutions

Alternate interior angles are equal, So, we have

⇒ (2x + 26) ° = (3x – 33) °

⇒ 2x + 26 = 3x – 33

x = 59

Substitute x in the original expressions.

⇒ (2x + 26) ° = 144°.

⇒ (3x – 33) ° = 144°

Hence proved, (2x + 26) ° = (3x – 33) °.

Example 4

Use alternate exterior angle theorem to prove that line 1 and 2 are parallel lines.

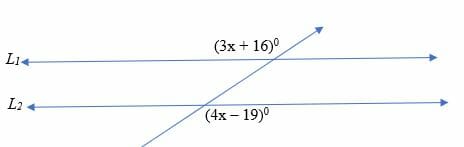
Solution

Line 1 and 2 are parallel if the alternating exterior angles (4x – 19) and (3x + 16) are congruent. Therefore;

⇒ 4x – 19 = 3x + 16

⇒ 4x – 3x = 19+16

x = 35

Hence, x = 35⁰

Substitute x in the expressions.

(4x – 19)⁰ ⇒ 4(35) – 19 = 121⁰

(3x + 16) = 121⁰

Therefore, line 1 and 2 are parallel

Interesting Facts about Alternate Exterior Angles

• Alternate exterior angles are congruent if the lines crossed by the transversal are parallel.
• If alternate exterior angles are congruent, then the lines are parallel.
• At each intersection, the corresponding angles lie at the same place.
• The alternate exterior angles that lie outside the lines are intercepted by the transversal.
• These angles are supplementary to the adjacent angles.

Applications of Alternate Exterior Angles

Alternate Exterior Angles are very important in our daily life.

For example:

• In engineering and architecture, alternate exterior angles are used to design buildings, bridges, roads etc.
• Another use of alternate exterior angles is in fitting items such as sofas, chairs, tables etc. into your home.
• In trigonometry, alternate exterior angles can be used to calculate the height of tall structures such as buildings.
• Alternate exterior angles are used to design regular polygons such as hexagons and many more shapes.

Other settings where alternate exterior angles are applied include; set squares, scissors, partly opened-doors, arrowhead, pyramids, different alphabetical letters, cycle spokes etc.

We even make different angles in different postures while doing yoga and exercises.