Alternate Interior Angles – Explanation & Examples

In this article, we are going to learn another special type of angle formed when parallel or non-parallel lines are intersected by a transversal line.

As you know, parallel lines are two or more lines which never meet, whereas, a transversal line is a straight line which intersects two or more parallel lines.

To know the other related definitions of angles and different types of angles, you can consult the previous articles.

What are the Alternate Interior Angles?

Alternate interior angles are angles formed when two parallel or non-parallel lines are intersected by a transversal. The angles are positioned at the inner corners of the intersections and lie on opposite sides of the transversal.

Alternate interior angles are equal if the lines intersected by the transversal are parallel. Alternate interior angles formed when a transversal crosses two non-parallel lines have no geometrical relation. Therefore, there is need to discuss angles here.

Illustration of alternate interior angles:

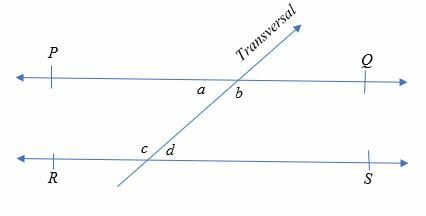
Consider the figure give above.

PQ and RS are the two parallel lines intersected by the transversal line. Therefore, the pairs of alternating interior angles are:

• ∠a & ∠ d
• ∠b & ∠

Hence, ∠a = ∠ d and ∠b = ∠c.

We can make the following observations about alternate interior angles:

• Alternate interior angles are congruent.
• Consecutive interior angles are supplementary. Consecutive interior angles are interior angles which are on the same side of the transversal line.
• Alternate interior angles don’t have any specific properties in the case of non – parallel lines.

Alternate Interior Angles Theorem

The alternate interior angles theorem states that, the alternate interior angles are congruent when the transversal intersects two parallel lines.

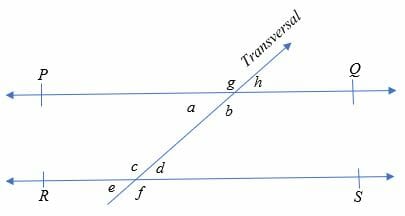
Proof of alternate interior angles theorem

Given: Line PQ//RS

To prove:∠ a = ∠d and ∠b = ∠c

Since we know that corresponding angles and vertical angles are equal to each when

a transversal crosses any two parallel lines. Therefore,

∠g = ∠c ………. (i) [Corresponding angles]

∠g = ∠b ………. (ii) [Vertically opposite angles]

From eq.(i) and (ii), we get;

∠b = ∠c [Alternate interior angles]

Similarly,

∠a = ∠d

Hence, it is proved.

How to find alternate interior angles

Alternate interior angles can be calculated by using properties of the parallel lines.

Example 1

Given two angles (4x – 19)⁰ and (3x + 16)⁰ are congruent alternate interior angles. Find the value of x and also determine the value of the other pair of alternate interior angles,

Solution

⇒ 4x – 19 = 3x + 16

⇒ 4x – 3x = 19+16

x = 35

Therefore, x = 35⁰

(4x – 19)⁰ ⇒ 4(35) – 19 = 121⁰

Since, angles formed on the same side of the transversal are supplementary angles. Then, the value of the other pair of alternate interior angles is;

⇒ 180⁰ – 121⁰= 59⁰

Example 2

Two consecutive interior angles are (2x + 10) ° and (x + 5) °. Find measure of the angles.

Solution

Consecutive interior angles are supplementary.

⇒ (2x + 10) ° + (x + 5) ° = 180°

⇒ 2x + 10 + x + 5 = 180

⇒ 3x + 15 = 180

Subtract 15 from both sides.

⇒ 3x = 165

Divide both sides by 3.

x = 55

Therefore, the consecutive interior angles are:

⇒ (2x + 10) ° = [2(55) + 10] ° = 120°

⇒ (x + 5) ° = 55 + 5° = 60°

Example 3

If (2x + 26) ° and (3x – 33) ° are alternate interior angles which are congruent, find the measurement of the two angles.

Solutions

Alternative interior angles are equal, So, we have

⇒ (2x + 26) ° = (3x – 33) °

⇒ 2x + 26 = 3x – 33

x = 59

The measurement of the angles is 144°.

Example 4

Find the value of x given that (3x + 20) ° and 2x° are consecutive interior angles.

Solution

Consecutive interior angles are supplementary, therefore;

⇒ (3x + 20) ° + 2x° = 180°

⇒3x + 20 + 2x = 180

⇒5x + 20 = 180

Subtract 20 from both sides

⇒5x = 160

Divide each side by 8.

x = 32

Hence, the value of x is 32 degrees.

The consecutive interior angles are therefore, 60° and 120°.

Applications of Alternate Interior Angles

• The most famous application of alternate interior angles is a famous Greek scientific writer, Eratosthenes, use alternate interior angles to prove that the Earth is round.
• The windows, with panes divided by mun-tins, have the alternate interior angles.
• In a letter Z, the top and bottom horizontal lines are parallel and diagonal line is transversal. So, there are two alternate interior angles in a letter Z.