Alternate Segment Theorem – Explanation & Examples
There exist several geometric properties and theorems about circles. Circle theorems are very useful because they are used in geometric proofs and to calculate angles.
You have studied the Inscribed Angle Theorem and Thales’ Theorem so far. In this article, you will learn about an interesting theorem known as the Alternate Segment Theorem. Like the other two theorems, this is also based on the angles.
What is the Alternate Segment Theorem?
The alternate segment theorem also referred to as the tangent-chord theorem, states that:
The angle measure between a chord of a circle and a tangent through any of the chord’s endpoints is equal to the measure of an angle in the alternate segment.
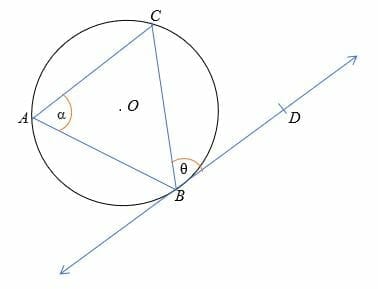
According to the alternate segment theorem, ∠CBD = ∠CAB
α = θ
Where α and θ are alternate angles.
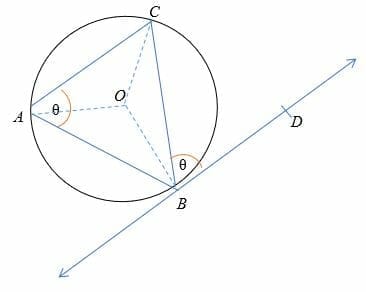
Proof of alternate segment theorem:
Let’s get a clear understanding of the theorem by making a few proofs.
- Join the ends of all the cords to the center of the circle. These will be the radii of the circle.
- Since, OB = OA = OC, then △OBCis isosceles, so we have
∠OCB =∠OBC
∠COB = 180°− ∠OCB − ∠OBC
= 180° − 2∠OBC ………………………(i)
- Since OB (radius) joins the tangent BD at point B, then ∠OBD = 90°
Therefore, θ = 90°− ∠OBC…………………. (ii)
By solving equation (i) and (ii), we get
∠COB =2θ
But, recall the inscribed angle theorem.
∠COB = 2∠BAC
2θ = 2∠BAC
Divide both sides by 2 to get,
∠BAC = θ
For a better understanding of the theorem, let’s work through some examples:
Example 1
Find the value of ∠QPS in the diagram shown below.
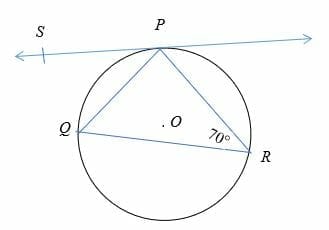
Solution
By alternate segment theorem,
∠QPS = ∠QRP
So, ∠QPS = 70°
Example 2
In the diagram below, ∠CBD = 56° and ∠ABC = 65°. What is the measure of ∠ACB?
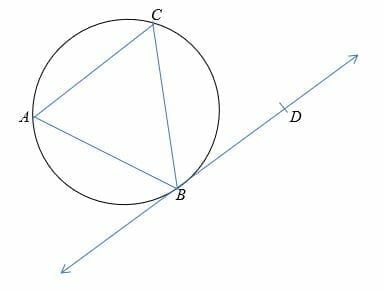
Solution
Alternate segment theorem tells us that,
∠CBD =∠BAC = 56°
And according to triangle sum theorem,
∠ABC + ∠ACB + ∠BAC = 180°
65° + ∠ACB + 56° = 180°
Simplify.
121° + ∠ACB = 180°
Subtract 121° on both sides.
∠ACB = 59°
Therefore, the measure of ∠ACB is 59°.
Example 3
In the diagram shown below, point C is the center of the circle with a radius of 8 cm and ∠QRS = 80°. Find the length of arc QTR.
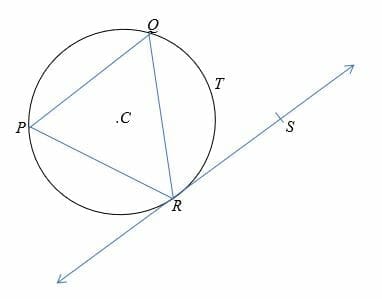
Solution
First, join the vertices of the triangle to the center.
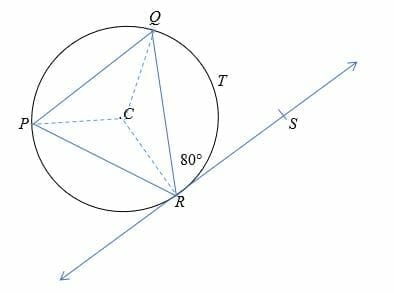
By alternate segment theorem, ∠QRS=∠QPR = 80°.
Recall the inscribed angle theorem, 2∠QPR = ∠QCR.
So, ∠QCR = 2 x 80°.
= 160°.
Arc length = 2πr(θ/360)
= 2 x 3.14 x 8 x (160/360)
= 22.33 cm.
Example 4
In the diagram below, point C is the center of the circle. If ∠AEG = 160° and ∠DEF =60°, find the measure of ∠EAB and ∠ BDE
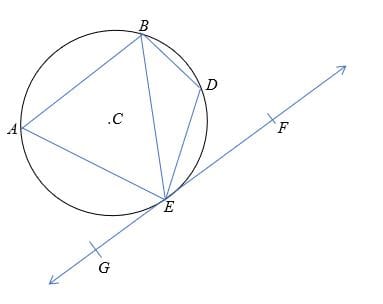
Solution
According to the tangent-chord theorem,
∠EAB = ∠DEF =60°
Similarly,
∠AEG = ∠ BDE = 160°
Example 5
Find the measure of angle x and y in the diagram below.
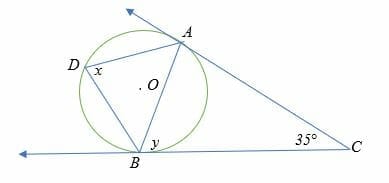
Solution
Length AB = BC (property of tangents)
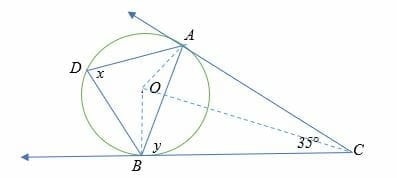
∠COA = 180° – (90 + 35°/2)
= 160° – 107.5°
= 72.5°
Therefore, ∠ AOB = 2 x 72.5°
= 145°
Recalling the inscribed angle theorem,
2x = ∠ AOB = 145°
x = 72.5°.
And by alternate segment theorem,
x = y = 72.5°
Example 6
In the diagram below, AB is the diameter of the circle. Find the measure of angles x, y, and z.
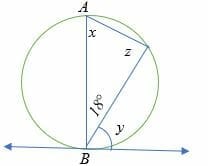
Solution
According to the inscribed angle theorem, z = 90°
And,
sum of interior angles of a triangle =180°
So, x = 180° – (90° + 18°)
x = 72°
Also, according to alternate segment theorem,
x = y = 72°
Therefore, the measure of angle x = y =72° and z = 90°
Example 7
Find the measure of ∠x and ∠y in the diagram below.
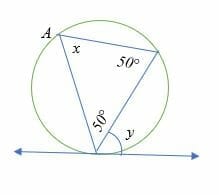
Solution
Sum of interior angles of a triangle = 180°.
50° + 50° + x = 180°
x = 180° – 100°
x = 80°
And according to alternate segment theorem,
x = y = 80°.
Therefore, the measure of ∠x and ∠y is 80°.
Example 8
Given ABC is 70 degrees and angle BCD is 66 degrees. What is the measure of angle x?
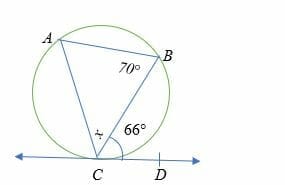
Solution
Angle BCD = angle CAB = 66° (Alternate segment theorem).
And sum of interior angles = 180°
70° + 66° + x = 180°
Simplify.
136° + x = 180°
Subtract 136° on both sides.
x = 44°.
Thus, the measure of angle x is 44°.
