JUMP TO TOPIC
Angles in a Circle – Explanation & Examples
The concept of angles is essential in the study of geometry, especially in circles. You have seen a few theorems related to circles previously that all involve angles in it.
Now, this article is purely related to the angles of a circle.
You will also learn how to find the measure of an angle in a circle. For the definition of angles and parts of circles, you can consult previous articles. You will also learn what the interior angle and exterior angle of a circle entail.
What is the Angle of a Circle?
What is the angle of a circle? Or, to be more precise, how can we form an angle inside a shape which does not have any edges?
The answer is that angles are formed inside a circle with radii, chords, and tangents. Let’s see it below. An angle of a circle is an angle that is formed between the radii, chords, or tangents of a circle.
We saw different types of angles in the “Angles” section, but in the case of a circle, there, basically, are four types of angles. These are central, inscribed, interior, and exterior angles. Let’s see each of them individually below.
The central angle is formed between two radii, and its vertex lies at the center of the circle.
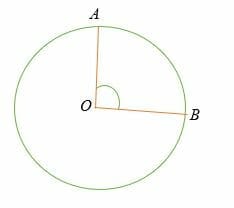
In the above diagram, ∠AOB = central angle
where arc AB is the intercepted arc.
In a circle, the sum of the minor and major segment’s central angle is equal to 360 degrees.
On the other hand, an inscribed angle is formed between two chords whose vertex lies in a circle’s circumference.
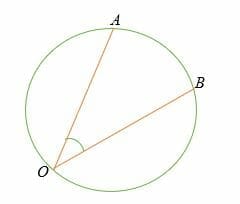
In the above illustration, ∠AOB is the inscribed angle.
How to Find the Measure of an Angle?
How to find the central angle:
The formula to find the central angle is given by;
Central angle = (Arc length x 360)/2πr
where r is the radius of a circle.
How to find the inscribed angle:
The formula for an inscribed angle is given by;
Inscribed angle = ½ x intercepted arc
We studied interior angles and exterior angles of triangles and polygons before. It is time to study them for circles as well.
Interior angle of a circle
An interior angle of a circle is formed at the intersection of two lines that intersect inside a circle.
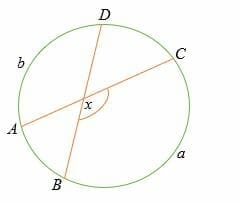
In the diagram above, if b and a are the intercepted arcs, then the measure of the interior angle x is equal to half the sum of intercepted arcs.
x = ½ (b + a)
Exterior angle of a circle
An exterior angle of a circle is an angle whose vertex is outside a circle, and the sides of the angle are secants or tangents of the circle.
The measure of an exterior angle is equal to half the difference of the measure of intercepted arcs.
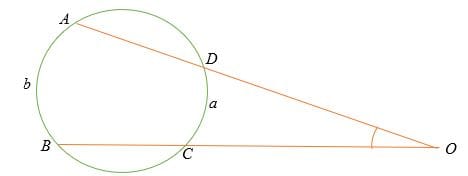
The formula for the exterior angle is given by
Exterior angle, ∠BOA = ½ (b – a)
Let work on a few examples:
Example 1
Find the central angle of a segment whose arc length is 15.7 cm and radius is 6 cm.
Solution
Central angle = (Arc length x 360)/2πr
Central angle = (15.7 x 360)/2 x 3.14 x 6
= 5652/37.68
= 150
Therefore, the central angle is 150 degrees.
Example 2
In the diagram below, the intercepted arcs are 60 degrees and 120 degrees, respectively. Find the measure of the exterior angle, x?
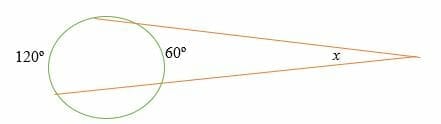
Solution
The exterior angle, x = ½ (b – a)
x = ½ (120º – 60º)
x = 30 º
So, the measure of the exterior angle is 30 degrees.
Example 3
Find the measure of the missing central angle in the following circle.
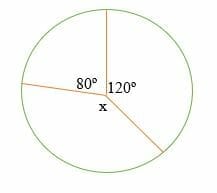
Solution
Sum of central angles in a circle = 360 º
80º + 120º + x = 360º
Simplify.
200º + x = 360º
Subtract by 200 º on both sides.
x = 160 º
Hence, the measure of the missing central angle is 160 degrees.
Example 4
What is the measure of ∠BOA and ∠AOE in the circle shown below?
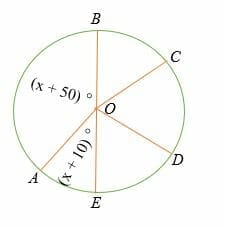
Solution
Since BE is a straight line (diameter of the circle) then,
∠BOA + AOE = 180°
(x + 50) ° + (x + 10) ° = 180°
2x + 60°= 180°
Subtract 60° on both sides.
2x = 120°
By dividing both side by 2, we get
x = 60°
Now substitute.
(x + 50) ° = 60° + 50°
= 110°
(x + 10) ° = 60° + 10°
= 70°
Hence, the measure of ∠BOA and ∠AOE is 110° and 70°, respectively.
Example 5
Find the interior angle of the following circle.
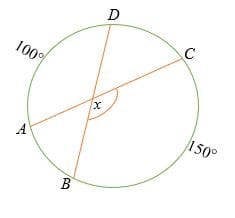
Solution
Given the measure of intercepted arcs as 150° and 100°.
Interior angle, x = ½ (150° + 100°)
= ½ x 250°
=125°
Thus, the interior angle is 125°.
