Angles in Polygons – Explanation & Examples

The polygon is not about the sides only. There may be scenarios when you have more than one shape with the same number of sides.

How to differentiate them then?
ANGLES!

The simplest example is that both rectangle and a parallelogram have 4 sides each, with opposite sides are parallel and equal in length. The difference lies in angles, where a rectangle has 90-degree angles on its all 4 sides while a parallelogram has opposite angles of equal measure.

In this article, you will learn:

• How to find the angle of a polygon?
• Interior angles of a polygon.
• Exterior angles of a polygon.
• How to calculate the size of each interior and exterior angle of a regular polygon.
   

How to Find the Angles of a Polygon?

We know that a polygon is a two-dimensional multi-sided figure made up of straight-line segments. The sum of angles of a polygon is the total measure of all interior angles of a polygon.

Since all the angles inside the polygons are the same. Therefore, the formula for finding the angles of a regular polygon is given by;

Sum of interior angles = 180° * (n – 2)

Where n = the number of sides of a polygon.

Examples

• Angles of a Triangle:

a triangle has 3 sides, therefore,

n = 3

Substitute n = 3 into the formula of finding the angles of a polygon.

Sum of interior angles = 180° * (n – 2)

= 180° * (3 – 2)

= 180° * 1

= 180°

• Angles of a Quadrilateral:

A quadrilateral is a 4-sided polygon, therefore,

n = 4.

By substitution,

sum of angles = 180° * (n – 2)

= 180° * (4 – 2)

= 180° * 2

= 360°

• Angles of a Pentagon

A pentagon is a 5 – sided polygon.

n = 5

Substitute.

Sum of interior angles = 180° * (n – 2)

=180° * (5 – 2)

= 180° * 3

= 540°

• Angles of an octagon.

An Octagon is an 8 – sided polygon

n = 8

By substitution,

Sum of interior angles = 180° * (n – 2)

= 180° * (8 – 2)

= 180° * 6

= 1080°

Angles of a Hectagon:

a Hectagon is a 100-sided polygon.

n = 100.

Substitute.

Sum of interior angles = 180° * (n – 2)

= 180° * (100 – 2)

= 180° * 98

= 17640°

Interior angle of polygons

The interior angle is an angle formed inside a polygon, and it is between two sides of a polygon.

The number of sides in a polygon is equal to the number of angles formed in a particular polygon. The size of each interior angle of a polygon is given by;

Measure of each interior angle = 180° * (n – 2)/n

where n = number of sides.

Examples

• Size of the interior angle of a decagon.

A decagon is a 10 -sided polygon.

n = 10

Measure of each interior angle = 180° * (n – 2)/n

Substitution.

= 180° * (10 – 2)/10

= 180° * 8/10

= 18° * 8

= 144°

• Interior angle of a Hexagon.

A hexagon has 6 sides. Therefore, n = 6

Substitute.

Measure of each interior angle =180° * (n – 2)/n

= 180° * (6 – 2)/6

= 180° * 4/6

= 60° * 2

= 120°

• Interior angle of a rectangle

A rectangle is an example of a quadrilateral (4 sides)

n = 4

Measure of each interior angle =180° * (n – 2)/n

=180° * (4 – 2)/4

=180° * 1/2

=90°

• Interior angle of a pentagon.

A pentagon is composed of 5 sides.

n = 5

The measure of each interior angle =180° * (5 – 2)/5

=180° * 3/5

= 108°

Exterior angle of polygons

The exterior angle is the angle formed outside a polygon between one side and an extended side. The measure of each exterior angle of a regular polygon is given by;

The measure of each exterior angle =360°/n, where n = number of sides of a polygon.

One important property about a regular polygon’s exterior angles is that the sum of the measures of the exterior angles of a polygon is always 360°.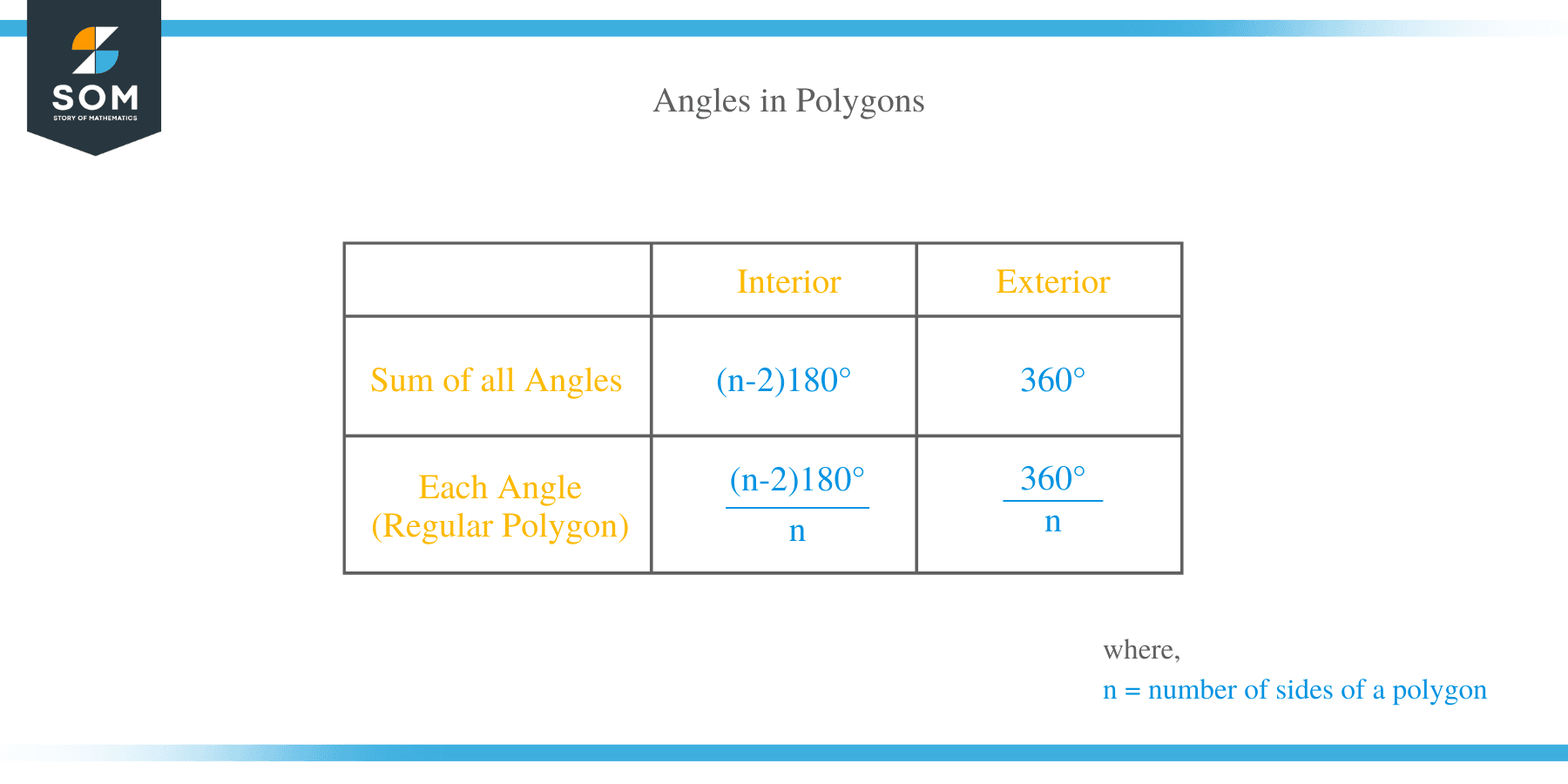

Examples

• Exterior angle of a triangle:

For a triangle, n = 3

Substitute.

Measure of each exterior angle = 360°/n

= 360°/3

= 120°

• Exterior angle of a Pentagon:

n = 5

Measure of each exterior angle = 360°/n

= 360°/5

= 72°

NOTE: The interior angle and exterior angle formulas only work for regular polygons. Irregular polygons have different interior and exterior measures of angles.

Let’s look at more example problems about interior and exterior angles of polygons.

Example 1

The interior angles of an irregular 6-sided polygon are; 80°, 130°, 102°, 36°, x°, and 146°.

Calculate the size of angle x in the polygon.

Solution

For a polygon with 6 sides, n = 6

the sum of interior angles =180° * (n – 2)

= 180° * (6 – 2)

= 180° * 4

= 720°

Therefore, 80° + 130° + 102° +36°+ x° + 146° = 720°

Simplify.

494° + x = 720°

Subtract 494° from both sides.

494° – 494° + x = 720° – 494°

x = 226°

Example 2

Find the exterior angle of a regular polygon with 11 sides.

Solution

n =11

The measure of each exterior angle= 360°/n

= 360°/11

≈ 32.73°

Example 3:

The exterior angles of a polygon are; 7x°, 5x°, x°, 4x° and x°. Determine the value of x.

Solution

Sum of exterior =360°

7x° + 5x° + x° + 4x° + x° =360°

Simplify.

18x = 360°

Divide both sides by 18.

x = 360°/18

x = 20°

Therefore, the value of x is 20°.

Example 4

What is the name of a polygon whose interior angles are each 140°?

Solution

Size of each interior angle = 180° * (n – 2)/n

Therefore, 140° = 180° * (n – 2)/n

Multiply both sides by n

140°n =180° (n – 2)

140°n = 180°n – 360°

Subtract both sides by 180°n.

140°n – 180°n = 180°n – 180°n – 360°

-40°n = -360°

Divide both sides by -40°

n = -360°/-40°

= 9.

Therefore, the number of sides is 9 (nonagon).