Angles of a Triangle – Explanation & Examples

We know that every shape in the universe is based on angles. The square is basically four lines connected so that each line makes an angle of 90 degrees with the other line. In this way, a square has four 90 degrees angles on its four sides.

Similarly, a straight line stretched on both sides at 180 degrees. If it turns at any point, it becomes two lines separated by a certain angle. In the same manner, a triangle is basically three lines connected at certain values of angles.

These measures of angles define the type of triangle. Therefore, angles are essential in studying any geometric shape.

In this article, you’ll learn the angles of a triangle and how to find the unknown angles of a triangle when you only know some of the angles. To know the important concepts of triangles, you can consult the previous articles.

What are the Angles of a Triangle?

The angle of a triangle is the space formed between two side lengths of a triangle. A triangle contains interior angles and exterior angles. Interior angles are three angles found inside a triangle. Exterior angles are formed when the sides of a triangle are extended to infinity.

Therefore, exterior angles are formed outside a triangle between one side of a triangle and the extended side. Each exterior angle is adjacent to an interior angle. Adjacent angles are angles with a common vertex and side.

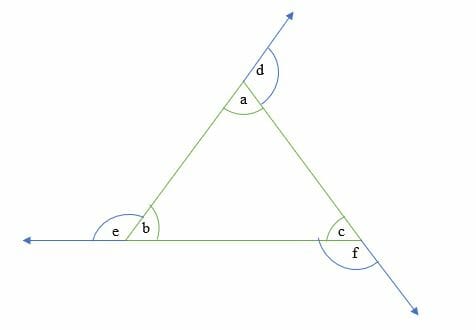
The figure below shows the angle of a triangle. The interior angles are a, b and c, while exterior angles are d, e, and f.

How to Find the Angles of a Triangle?

To find the angles of a triangle, you need to recall the following three properties about triangles:

• Triangle angle sum theorem: This states that the sum of all the three interior angles of a triangle is equal to 180 degrees.

a + b + c = 180º

• Triangle exterior angle theorem: This states that the exterior angle is equal to the sum of two opposite and non-adjacent interior angles.

f = b + a

e = c + b

d = b + c

• Straight line angles. The measure of angles on a straight line is equal to 180º

c + f = 180º

a + d = 180º

e + b = 180º

Let’s work out a few example problems.

Example 1

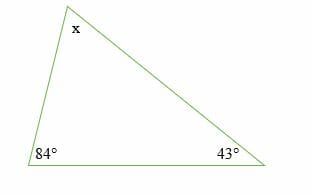
Calculate the size of the missing angle x in the triangle below.

Solution

By triangle angle sum, theorem, we have,

x + 84º + 43º = 180º

Simplify.

x + 127º = 180º

Subtract 127º on both sides.

x + 127º – 127º = 180º – 127º

x = 53 º

Hence, the size of the missing angle is 53º.

Example 2

Find the size of the interior angles of a triangle that form consecutive positive integers.

Solution

Since, a triangle has three interior angles, then, let the consecutive angles be:

⇒1^ST angle = x

⇒ 2^ND angle = x + 1

⇒3^RD angle = x + 2

But we know that, the sum of the three angles is equal to 180 degrees, therefore,

⇒ x + x + 1 + x + 2 = 180°

⇒ 3x + 3 = 180°

⇒ 3x = 177°

x = 59°

Now, substitute the value of x in the original three equations.

⇒1^ST angle = x = 59°

⇒ 2^ND angle = x + 1 =59° + 1 = 60°

⇒3^RD angle = x + 2 = 59°+ 2 = 61°

So, the triangle’s consecutive interior angles are; 59°, 60°, and 61°.

Example 3

Find the triangle’s interior angles whose angles are given as; 2y°, (3y + 15) ° and (2y + 25) °.

Solution

In triangle, um of interior angles = 180°

2y° + (3y + 15) ° + (2y + 25) ° = 180°

Simplify.

2y + 3y + 2y + 15° + 25° = 180°

7y + 40° = 180°

Subtract 40° on both sides.

7y + 40° – 40° = 180° – 40°

7y = 140°

Divide both sides by 7.

y = 140/7

y = 20°

Substitute,

2y°= 2(20) ° = 40°

(3y + 15) ° = (3 x 20 + 15) ° = 75°

(2y + 25) ° = (2 x 20 + 25) ° = 65°

So, the three interior angles of a triangle are 40°, 75°, and 65°.

 Example 4

Find the value of the missing angles in the diagram below.

Solution

By triangle exterior angle theorem, we have;

(2x + 10) ° = 63° + 87°

Simplify

2x + 10° = 150°

Subtract 10° on both sides.

2x + 10° – 10 = 150° – 10

2x = 140°

Divide both sides by 2 to get;

x = 70°

Now, by substitution;

(2x + 10) ° = 2(70°) + 10 ° = 140 ° + 10 ° = 150 °

Hence, the exterior angle is 150 °

But, straight line angles add up to 180 °. So, we have;

y + 150 ° = 180 °

Subtract 150 ° on both sides.

y + 150 ° – 150 ° = 180 ° – 150 °

y = 30 °

Therefore, the missing angles are 30 ° and 150 °.

Example 5

The interior angles of a triangle are in the ratio 4: 11: 15. Find the angles.

Solution

Let x be the common ratio of the three angles. So, the angles are,

4x, 11x and 15x.

In a triangle, sum of the three angles = 180°

4x + 11x + 15x = 180°

Simplify.

30x = 180°

Divide 30 on both sides.

x =180°/30

x = 6°

Substitute the value of x.

4x = 4(6) ° = 24°

11x = 11(6) ° = 66°

15x = 15(6) ° = 90°

So, the angles of the triangle are 24°, 66°, and 90°.

Example 6

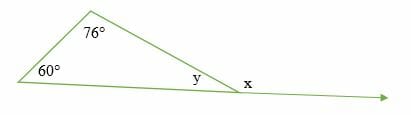
Find the size of angles x and y in the diagram below.

Solution

Exterior angle = sum of two non-adjacent interior angles.

60° + 76° = x

x = 136°

Similarly, sum of interior angles = 180°. Therefore,

60° + 76° + y = 180°

136° + y = 180°

Subtract 136° on both sides.

136° – 136° + y = 180° – 136

y = 44°

Hence, the size of angle x and y is 136° and 44°, respectively.

Example 7

The three angles of a certain triangle are such that the first angle is 20 % less than the second angle, and the third is 20% more than the second angle. Find the size of the three angles.

Solution

Let the second angle be x

First angle = x – 20x/100 = x – 0.2x

Third angle = x + 20x/100 = x + 0.2x

Sum of the three angles = 180 degrees.

x + x – 0. 2x + x + 0.2x = 180°

Simplify.

3x = 180°

x = 60°

Therefore,

2^nd second angle = 60°

1^st angle =48°

3^rd angle = 72°

So, the three angles of a triangle are 60°, 48°, and 72°.

Example 8

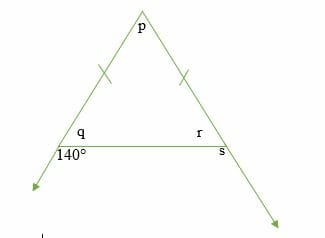
Calculate the size of angle p, q, r and s in the diagram below.

Solution

exterior angle = sum of the two non-adjacent interior angles.

140° = p + r …………. (i)

This is an isosceles triangle, so,

q = r

Angles on a straight line = 180°

140° + q = 180°

subtract 140 from both sides to get.

q = 40°

But q = r, so r is also 40°

r + s = 180° (linear angles)

40° + s =180°

s = 140°

Sum of interior angles = 180°

p + q + r = 180°

p + 40° + 40° = 180°

p = 180° – 80°

p = 100°