Angles – Explanation & Examples

What is Angle?

Angles are useful in our daily life, so it’s important to learn and understand them. For example, the minute hand of a wall clock turns angle 360 degrees to make a minute.

It takes the earth 24 hours to rotate at an angle of 360°. And that’s how the clocks are designed to synchronize with the rotation of the Earth. For many such reasons, it is, therefore, necessary to study angles.

In mathematics, an angle is defined as a geometric figure created by two rays sharing a common end point. The rays or lines that join or intersect at a common point to form an angle are referred to as sides of the angle.

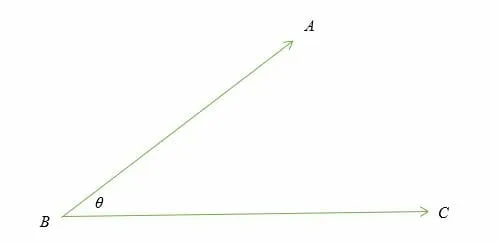
The units for measuring angles are the degree (°) and radian (rad). Angles are represented using the symbol ∠ and the Greek letters such as θ, α, etc.

For example, ∠ ABC = θ. Here, points A and C are the sides of the angle, while B is the vertex of the lines.

The concept of measurement of angles is dated back to 1500 BC in Egypt, where it took the Sun’s shadows against graduations marked on stone tablets. You can see the best evidence of this method in the Egyptian Museum found in Berlin.

A shadow was cast over a graduated stone tablet using a vertical rod known as “Gnomon.” With this method, Egyptians were able to measure time and seasons accurately.

How to Measure Angles?

The modern way of measuring an angle is by the use of a protractor. A protractor is a transparent glass or plastic tool with calibrations in either in radian or degree scale. You can read angles from a protractor either by moving clockwise or anticlockwise.

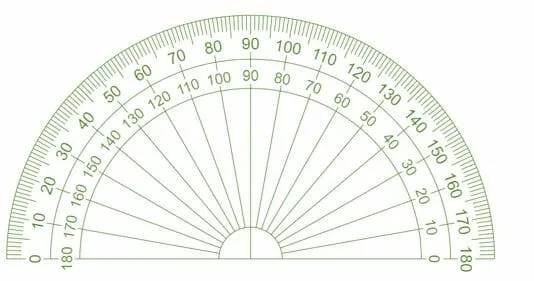
To measure an angle using a protractor, line up one line or ray along the protractor’s zero-degree line. Make sure the vertex of lines coincides with the midpoint of the protractor.

Finally, follow the second line to read to the nearest degree the size of the angle.

Example 1

To measure angle “α = 30^o” between two lines, proceed as follows:

Line up one line along the 0° mark on the protractor and follow the second line to read the angle.

∠ a = 30°

Example 2

Line up one line along the 0° mark on the protractor and follow the second line to read the angle.

∠ β = 90°

How to Draw Angles?

Angles less than 180° can be drawn using a protractor by following the steps below:

• Draw a straight line of any measurement. The straight line will act as the arm of the angle.
• Mark a dot at any position on the line. The dot will represent the vertex of the angle.
• Place the middle of the protractor at the vertex dot and ensure the mark on the line and the protractor flashes center.
• Find the given angle on the protractor scale and mark a small dot at the protractor’s edge.
• Now, remove the protractor and then use a ruler to join the dot with the vertex mark.
• Label the angle with capital letters

Example 3

Draw ∠ ABC = 50°

Explanation

• Draw a straight line of any dimension and place a dot along the line.

• Place the base of the protractor on the line such that its center coincides with the mark.

• Move anticlockwise along the protractor scale and place a dot at 50°.
• Using a ruler, join the dot with the mark on the line.
• Label your diagram such that A and C are the sides and B is the vertex of the angle.

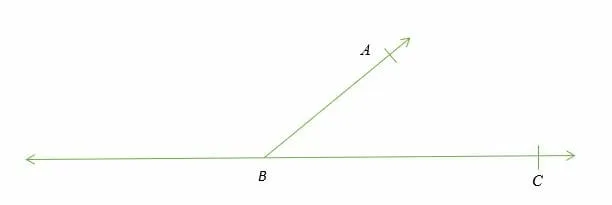
You can use the same procedure to draw any angle less than 180°.

Angles Pairs

Angle pairs are angles that appear in twos to display a certain geometrical property.

Some of the angle pairs include:

• Complementary angles
• Supplementary angles
• Vertical angles
• Alternate interior angles and alternate exterior angles
• Corresponding angles
• Adjacent angles.

Complementary angles

Two angles are said to be complementary to each other if their sum equals 90° (right angle).

Illustration of complementary angles.

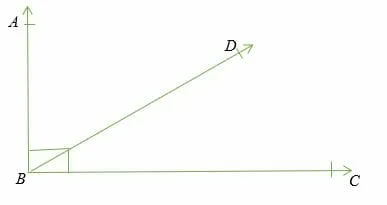
∠ ABD is a compliment of ∠ DBC because; ∠ ABD + ∠ DBC =90° (right angle).

Examples of complementary angles:

• 40° and 50°
• 60° and 30°
• 85° and 5°
• 70° and 20°
• 45° and 45° etc.

Supplementary angles

∠ ABD is a supplement of ∠ DBC because; Supplementary angles are pair angles whose sum of degree measurements equals 180° (straight line).

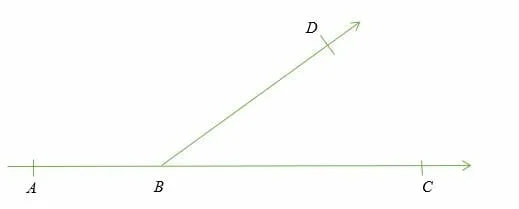
∠ ABD + ∠ DBC = 180° (straight line).

Some of the examples of supplementary angles include:

• 140° and 40°
• 120° and 60°
• 30° and 150°
• 90° and 90° etc.

Vertical angles

Vertical angles are pair angles formed by two intersecting lines such that the angles are opposite to each other.

Illustration:

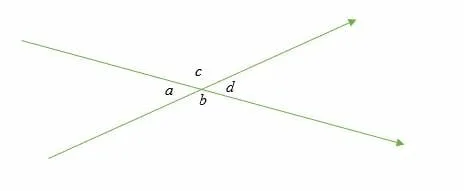
• ∠ a = ∠ d and are vertical angles
• ∠ c = ∠ b and are vertical angles

Alternate Interior Angles

Alternate interior angles are pair angles formed when a line intersects two parallel lines. Alternate interior angles are always equal to each other.

Illustration:

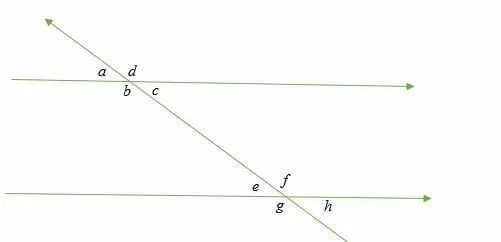
From the above diagram, alternate angles are:

• ∠ c and ∠ e
• ∠ b and ∠ f

Alternate Exterior Angles:

Alternate exterior angles are vertical angles of the alternate interior angles. Alternate exterior angles are equivalent.

Illustration:

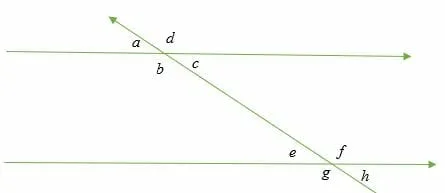
Alternate exterior angles are:

• ∠ a and ∠ h
• ∠ d and ∠ g

Corresponding Angles:

Corresponding angles are pair angles formed when a line intersects a pair of parallel lines. Corresponding angles are also equal to each other.

Illustration:

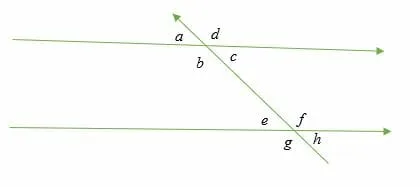
Pairs of corresponding angles from the above diagram are:

• ∠ a and e
• ∠ d and ∠ f
• ∠ c and ∠ h
• ∠ b and ∠g

Adjacent angles

Adjacent angles are pair angles that are next to one another.  They share a common vertex and side.

Illustration:

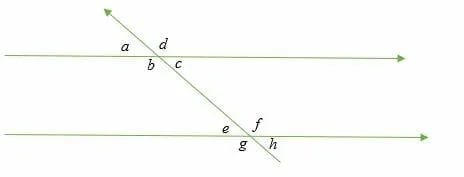
Some of the examples of adjacent angles from the above figure are:

∠ a and ∠ d

∠ d and ∠ c

∠ c and ∠ b etc.

Example 6

Given that ∠ a = 45°, find all the other angles in the diagram below.

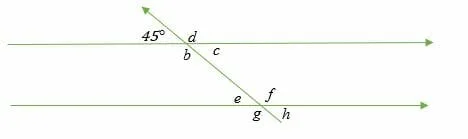
Solution

Given ∠ a = 45°

∠ a and ∠ d are supplementary angles (add up to 180°). Therefore ∠ d = 180° – 45°

∠ d = 135°

∠ a and ∠ c are vertical angles, and vertical angles are equal. Therefore ∠ c = 45°.

∠ d = 135° and ∠ b are vertical angles.

∠ b = 135°

∠ a = ∠ e = 45° (corresponding angles)

∠ d and ∠ f = 135° (corresponding angles)

∠ b =∠ g= 135° (corresponding angles.

∠ c = ∠ h = 45° (corresponding angles)