Antiderivative – Definition, Techniques, and Examples

Knowing how to find antiderivatives is one of the most important techniques that we’ll be learning in our integral calculus classes. In Physics, for example, we can find the function of the velocity given the function for the object’s acceleration. Given the rate of increase or decrease from a specimen, a researcher can find the original quantity or population. We can list more applications, but yes, these are all thanks to antiderivatives.

What if we’re given the function’s derivative, $\boldsymbol{f(x)}$, and this time, we need to find the function’s expression? We can work backwards and find an expression for the function, $\boldsymbol{F(x)}$. This is the foundation of antiderivatives: $\boldsymbol{F(x)}$ is the antiderivative of $\boldsymbol{f(x)}$.

In this article, we’ll show you how derivatives and antiderivatives are related to each other. We’ll also learn about the different antiderivatives that will come in handy when finding the antiderivative of a given function. You’ll also be able to test out your understanding of the exercises that follow!

What is an antiderivative?

The antiderivative of a function simply the result of reversing the derivative of a given function. When we have $F(x)$, it is considered the antiderivative of $f(x)$ when $\boldsymbol{F^{\prime}(x) = f(x)}$, for all values of $x$ within the allowed domain.  To better understand the definition of antiderivatives, try listing down at least three functions, $\{F_1(x), F_2(x), F_3(x)\}$, where all three functions have $x^3$ as its derivative.

A great guess would be $F(x) = x^4$, but if we try to differentiate this using the power rule, we’ll end up with  $F^{\prime}(x) = 4x^3$. To account for the coefficient, $F(x)$ must have $\dfrac{1}{4}$ as its constant factor. Hence, $F(x) = \dfrac{1}{4}x^4$. Now, how do we list down three unique functions? Recall that the derivative of constant will always be zero, so we simply add a unique constant to $F(x)$:

This shows that a function may have multiple antiderivatives since we can add any constant after the antiderivative, $F(x)$, and the derivative function, $f(x)$, will still be the same.

Here’s a helpful guide to remember how derivatives and antiderivatives are related to each other:

\begin{aligned} F^{\prime}(x) &= f(x)\end{aligned}

This means that finding the antiderivative is simply reversing the process of finding the function’s derivative.

The general form of the antiderivative

In the previous table, we’ve shown you that there can be multiple possible antiderivatives for one given function. That’s because expressions with identical terms except for their constants will have identical derivatives.

\begin{aligned}F^{\prime} (x) = f(x) = G^{\prime} (x) \end{aligned}

Let’s say we have $F(x)$ and $G(x)$, where the two functions only vary by a constant $C$. This means that they’ll be sharing a common derivative, $f(x)$. Since $F(x)$ and $G(x)$ differ by $C$, we can rewrite $G(x)$ as $F(x) +C$.

This generalizes the antiderivatives  of $f(x)$ as $F(x) + C$, where $C$ is an arbitrary constant.

\begin{aligned}F^{\prime}(x) &= f(x) \\\text{Indefinite Integral of }f(x) &= F(x) + C\end{aligned}

This is the general form of a function’s antiderivative. Keep in mind that $C$ is an arbitrary constant and $\boldsymbol{F(x) +C}$ is the antiderivative of $\boldsymbol{f(x)}$. The process of antidifferentiation is simply finding the function’s antiderivative.

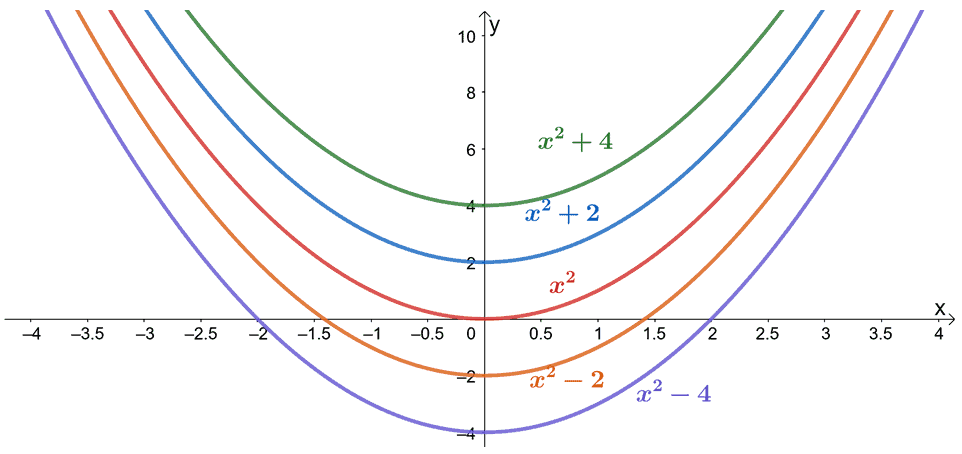
Here’s an example of a family of antiderivatives that shared the same derivative of $2x$. From this, we can see that that the functions of the form $x^2 + C$ will always have a derivative of $2x$.

Integration and indefinite integral

Integration and antidifferentitation are interchangeable processes since we’re performing the same process for both. We can also represent antiderivatives using the integration symbol, $\int$. When $f(x)$ is a function with an antiderivative of $F(x)$, we have the relationship shown below:

\begin{aligned}\int f(x) \phantom{x}dx &= F(x) + C\end{aligned}

This means that $\int f(x) \phantom{x}$ and $F(x) +C$ both represent the antiderivative or indefinite integral of $f(x)$.

Using our earlier example, since $\dfrac{d}{dx} \dfrac{1}{4}x^4 = x^3$, we have $\int x^3 \phantom{x}dx = \dfrac{1}{4}x^4 + C$.

This is a more common format for antiderivatives, so make sure to familiarize yourself with rewriting antiderivatives using the symbol, $\int$. We call this the integral symbol. The function that’s being integrated is called the integrand.

How to find the antiderivative?

One way for us to find the antiderivative of a function is by working backward and recalling a derivative rule that may have been applied. Given $f(x)$, we’ll need to think of a function, $F(x)$, that satisfies the condition, $F^{\prime}(x)=  f(x)$.

For example, if we want to find the antiderivative of $y =6$, we’re simply looking for a function that when differentiated, returns $6$. Recall that when we have $kx$, $\dfrac{d}{dx} kx = k$, where $k$ is a constant. This means that the antiderivative of $y = 6$ is $6x +C$.

\begin{aligned}\dfrac{d}{dx} 6x &= 6\\ \int 6\phantom{x}dx &= 6x + C\end{aligned}

We can apply a similar process to derive the different integral rules and antiderivative formulas. Below are a few examples of integral rules derived from known derivative rules.

\begin{matrix} \dfrac{d}{dx} \sin x = \cos x & \Rightarrow  & \int \cos x \phantom{x}dx = \sin x + C \\\dfrac{d}{dx} \cos x = -\sin x & \Rightarrow  & \int -\sin x \phantom{x}dx = \cos x + C \\ \dfrac{d}{dx} e^x = e^x & \Rightarrow  & \int e^x \phantom{x}dx = e^x + C\\\dfrac{d}{dx} \dfrac{1}{n + 1} \cdot x^{n + 1} = x^n & \Rightarrow  & \int x^n \phantom{x}dx = \dfrac{x^{n + 1}}{n + 1} + C\end{matrix}

When finding the integral of more complex functions, combine indefinite integral properties and antiderivative rules. For now, take a look at this comprehensive list of helpful antiderivative rules.

List of antiderivative formulas

Here’s a list of integral or antiderivative formulas that will be handy when finding the antiderivative of a function. We’re showing the derivative rule used to come up with each integration rule shown to highlight how closely related these two concepts are.

Here’s a list of integral or antiderivative formulas that will be handy when finding the antiderivative of a function. We’re showing the derivative rule used to come up with each integration rule shown to highlight how closely related these two concepts are.

Applying the antiderivative formulas to integrate a function

Keep the formulas handy especially when integrating complex functions. By complex functions, we mean functions that may require two or more antiderivative rules before we can integrate the complex function.

Aside from these antiderivative rules, these three integral properties will come in handy when integrating complex functions.

\begin{aligned}\int k\cdot f(x)\phantom{x}dx &= k \int f(x)\phantom{x}dx\\\int [f(x) + g(x)] \phantom{x}dx &= \int f(x)\phantom{x} dx + \int g(x)\phantom{x} dx\\\int [f(x) – g(x)] \phantom{x}dx &= \int f(x)\phantom{x} dx – \int g(x)\phantom{x} dx \end{aligned}

These three properties are similar to the constant multiple, sum, and different properties of differentiation. We’ve actually discussed further these interesting properties in this article, so check it out if you want a more in-depth discussion regarding integral properties.

Follow the guide shown below whenever you need to integrate functions that contain multiple terms.

• Factor out the constants of the integrals whenever possible.
• Distribute the $\int$ symbol using the sum and difference properties of integration.
• Apply appropriate antiderivative formulas to each group of terms.

Let’s try finding the antiderivative of $f(x) = x^4 – 3x^3 + 4x^2 – 8$. Meaning, we need to evaluate $\int x^4 – 3x^3 + 4x^2 – 8 \phantom{x} dx$. Begin by distributing the integral operation then factoring out the constants from $3x^3$ and $4x^2$.

\begin{aligned}\int x^4 – 3x^3 + 4x^2 -8 \phantom{x} dx &= \int x^4\phantom{x} dx – \int3x^3\phantom{x} dx + \int 4x^2\phantom{x} dx -\int8 \phantom{x} dx\\&= \int x^4\phantom{x} dx – 3\int x^3\phantom{x} dx + 4\int x^2\phantom{x} dx -\int 8 \phantom{x} dx\end{aligned}

At this point, we’ll have to rely on the antiderivative formulas to simplify each term.

• Apply the antiderivative formula, $\int x^n \phantom{x}dx = \dfrac{x^{n + 1}}{n + 1} + C$, to simplify the first three terms.

• Use the antiderivative formula, $\int k \phantom{x}dx = kx + C$, to simplify the fourth term.

\begin{aligned}\int 8\phantom{x} dx&= 8x + C\end{aligned}

• Since $C$ represents an arbitrary constant, we can simply use one $C$ at the end.

\begin{aligned}\int x^4 – 3x^3 + 4x^2 -8 \phantom{x} dx &= \dfrac{1}{5}x^5 – 3\cdot \dfrac{x^{3 + 1}}{3 + 1} + 4\cdot \dfrac{x^{2 + 1}}{2 + 1} – 8x + C\\&= \dfrac{1}{5}x^5 – \dfrac{3}{4}x^4 + \dfrac{4}{3}x^3 – 8x + C\end{aligned}

Hence, we’ve shown you how to integrate $f(x) = x^4 – 3x^3 + 4x^2 – 8$ using the different integral properties and formulas. We have shown that $\int x^4 – 3x^3 + 4x^2 -8 \phantom{x} dx = \dfrac{1}{5}x^5 – \dfrac{3}{4}x^4 + \dfrac{4}{3}x^3 – 8x + C$.

Apply similar processes when integrating the functions shown in the exercises below. But before that, make sure to take note of the antiderivative formulas we’ve provided as we’ll needing most of them in the examples shown.

Example 1

Find the antiderivatives of the following functions:

a. $\int x^4 \phantom{x}dx$
b. $\int \dfrac{1}{x^3} \phantom{x}dx$
c. $\int \sqrt{x} \phantom{x}dx$
d. $\int \dfrac{1}{x^e} \phantom{x}dx$

Solution

All four functions contain only one term. Each term contains a base of $x$ and an exponent, so we’ll use the power rule for integration: $\int x^n \phantom{x} dx = \dfrac{x^{n + 1}}{n + 1} + C$.

• Find the antiderivative by increasing the exponent by $1$.
• Divide the resulting expression by new exponent of $x$.
• Include a “$ + C$” after the antiderivative to cover all functions belonging in the same family.

Let’s go ahead and evaluate $\int x^4 \phantom{x}dx$ using this approach.

\begin{aligned}\int x^4 \phantom{x}dx &= \dfrac{x^{4 + 1}}{4 + 1} + C\\&= \dfrac{x^5}{5} + C \end{aligned}

Rewrite $\dfrac{1}{x^3}$ as a power of $x$: $\dfrac{1}{x^3} = x^{-3}$. With this form, we can find the antiderivative of the second function using the power rule.

\begin{aligned}\int \dfrac{1}{x^3} \phantom{x}dx &=\int x^{-3}\phantom{x}dx\\&= \dfrac{x^{-3 + 1}}{-3 + 1} + C\\&= \dfrac{x^{-2}}{-2} + C\\&= -\dfrac{1}{2x^2} + C \end{aligned}

We’ll apply a similar process for the third item. Use the fact that $\sqrt{x} = x^{\frac{1}{2}}$.
\begin{aligned}\int \sqrt{x} \phantom{x}dx &=\int x^{\frac{1}{2}}\phantom{x}dx\\&= \dfrac{x^{\frac{1}{2} + 1}}{\dfrac{1}{2} + 1} + C\\&= \dfrac{x^{\frac{3}{2}}}{\dfrac{3}{2}} + C\\&= \dfrac{2}{3}x^{\frac{3}{2}} + C \end{aligned}

For the fourth function, we’ll still be using the power rule and treat $e$ as a constant found at the exponent. Begin by rewriting $\dfrac{1}{e^x}$ as $x^{-e}$.

\begin{aligned}\int\dfrac{1}{ x^e} \phantom{x}dx &=\int x^{-e}\phantom{x}dx\\&= \dfrac{x^{-e + 1}}{-e + 1} + C\\&= \dfrac{1 – x^e}{1 – e}+ C \end{aligned}

Hence, we have the following antiderivatives:

a. $\int x^4 \phantom{x}dx = \dfrac{x^5}{5} + C$
b. $\int \dfrac{1}{x^3} \phantom{x}dx = -\dfrac{1}{2x^2} + C$
c. $\int \sqrt{x} \phantom{x}dx = \dfrac{2}{3}x^{\frac{3}{2}} + C $
d. $\int \dfrac{1}{x^e} \phantom{x}dx = \dfrac{1 – x^e}{1 – e}+ C $

Example 2

Find the antiderivatives of the following functions:

a. $\int 4x^3 \phantom{x}dx$
b. $\int \dfrac{1}{3x^2} \phantom{x}dx$
c. $\int (4x^2 – 2x + 5) \phantom{x}dx$
d. $\int (\sin x – \cos x) \phantom{x}dx$

Solution

Each of the four functions requires two or more rules of integration. We’ll break down the process for each item and include the antiderivative formulas used.

Let’s begin working on the first function – $\int 4x^3 \phantom{x}dx$.

• Factor out $4$ from the integral expression using the integral property, $\int k f(x)\phantom{x} dx = k \int f(x)\phantom{x}dx$.
• Integrate the expression, $\int x^3 \phantom{x} dx$, using the power rule: $\int x^n \phantom{x} dx = \dfrac{x^{n + 1}}{n + 1} + C$.

\begin{aligned}4x^3 \phantom{x}dx &=4\int x^3\phantom{x}dx\\&= 4 \cdot \dfrac{x^{3 + 1}}{3 + 1} + C\\&= 4 \cdot \dfrac{x^4}{4}+ C\\&= x^4 + C \end{aligned}

For the second function, rewrite $\dfrac{1}{3x^2}x$ as $\dfrac{1}{3} x^{-2}$ first. Use the same rules to find its antiderivative.

\begin{aligned}\int \dfrac{1}{3x^2}  \phantom{x}dx &=\int \dfrac{1}{3}x^{-2}\phantom{x}dx\\&=\dfrac{1}{3}\int x^{-2} \phantom{x}dx\\&= \dfrac{1}{3} \cdot \dfrac{x^{-2 + 1}}{-2 + 1} + C\\&= \dfrac{1}{3} \cdot \dfrac{x^{-1}}{-1}+ C\\&= -\dfrac{1}{3x} + C \end{aligned}

For the third function, apply the sum and difference properties first. Integrate each of the term using the constant multiple and power rules.

• Distribute the integral operation to each term.
• Factor out $4$ and $2$ out of the integrands and apply the antiderivative formula, $\int x^n \phantom{x} dx = \dfrac{x^{n + 1}}{n + 1} + C$.
• Integrate the third expression using the integration rule, $\int k \phantom{x}dx = kx +C$.

\begin{aligned}\int (4x^2 -2x + 5) \phantom{x} dx &= \int 4x^2 \phantom{x} dx – \int 2x \phantom{x} dx +\int 5\phantom{x} dx \\&= 4\int x^2 \phantom{x} dx – 2\int x \phantom{x} dx +\int 5\phantom{x} dx\\&= 4 \cdot \dfrac{x^{2 + 1}}{2 + 1} – 2 \cdot \dfrac{x^{1 + 1}}{1 + 1}+\int 5 \phantom{x}dx\\&= \dfrac{4}{3}x^3 – x^2 + 5x + C\end{aligned}

Before working on the fourth function, recall that $\int \sin x \phantom{x}dx = – \cos x$ and $\int \cos x \phantom{x}dx = \sin x$. Use these two antiderivative formulas when finding the antiderivative of the function.

\begin{aligned}\int (\cos x – \sin x) \phantom{x} dx &= \int \cos x \phantom{x} dx – \int \sin x \phantom{x} dx\\&= (-\sin x) – (\cos x) + C\\ &= -\sin x – \cos x + C\end{aligned}

Hence, we have the following antiderivatives:

a. $\int 4x^3 \phantom{x}dx = x^4 + C $
b. $\int \dfrac{1}{3x^2} \phantom{x}dx = -\dfrac{1}{3x} + C $
c. $\int (4x^2 – 2x + 5) \phantom{x}dx = \dfrac{4}{3}x^3 – x^2
+ 5x + C $
d. $\int (\sin x – \cos x) \phantom{x}dx= -\sin x – \cos x + C$

Example 3

Find the antiderivative of the function $f(x) = \dfrac{x^6 – 3x^4 + 1}{x^3}$.

Solution

We want to find $\int \dfrac{x^6 – 3x^4 + 1}{x^3} \phantom{x}          dx$. We don’t have  an equivalent quotient rule for integration, so what we can do is rewrite the integrand by dividing each term of the numerator by the denominator.

\begin{aligned}\int \dfrac{x^6 -3x^4 + 1}{x^3} \phantom{x}dx &=\int \left(\dfrac{x^6}{x^3} -\dfrac{3x^4}{x^3} + \dfrac{1}{x^3}\right )\phantom{x}dx\\&= \int \left(x^3 – 3x + \dfrac{1}{x^3}\right) \phantom{x}dx \end{aligned}

Focus on each of the integral expressions and use the different antiderivative rules we’ve just learned to evaluate each expression.

Going back to our previous expression, distribute the integral operation and use the antiderivatives shown above:

\begin{aligned}\int x^3\phantom{x}dx – \int3 x\phantom{x}dx + \int\dfrac{1}{x^3} \phantom{x}dx &= \left(\dfrac{x^4}{4}  \right ) – \left(\dfrac{3x^2}{2}\right ) + \left(-\dfrac{1}{2x^2}\right ) + C\\&= \dfrac{x^4}{4} – \dfrac{3x^2}{2}- \dfrac{1}{2x^2} + C\end{aligned}

Hence, the antiderivative of $f(x)$ is equal to $\dfrac{x^4}{4} – \dfrac{3x^2}{2}- \dfrac{1}{2x^2} + C$.

Practice Questions

1. Find the antiderivatives of the following functions:
a. $\int x^5 \phantom{x}dx$
b. $\int \dfrac{1}{x^4} \phantom{x}dx$
c. $\int \sqrt[3]{x^2} \phantom{x}dx$
d. $\int \dfrac{1}{x^{\pi}} \phantom{x}dx$

2. Find the antiderivatives of the following functions:
a. $\int -6x^5 \phantom{x}dx$
b. $\int \dfrac{1}{3x^4} \phantom{x}dx$
c. $\int (3x^4 – 6x^2 + 12) \phantom{x}dx$
d. $\int (\dfrac{1}{x} – \sec^2 x) \phantom{x}dx$

3. Find the antiderivatives of the following functions:
a. $\int 6\sqrt{x} – \sqrt[5]{x} \phantom{x}dx$
b. $\int \dfrac{4x^3 – 5}{x^2} \phantom{x}dx$
c. $\int (3e^x – 8\sec^2 x) \phantom{x}dx$
d. $\int \dfrac{6 – 5x^6 – 2x^3}{x^3} \phantom{x}dx$

Answer Key

1.
a. $\int x^5 \phantom{x}dx = \dfrac{x^6}{6} + C$
b. $\int \dfrac{1}{x^4} \phantom{x}dx = -\dfrac{1}{3x^3} + C$
c. $\int \sqrt[3]{x^2} \phantom{x}dx = \dfrac{3}{5}x^{\frac{5}{3}} + C$
d. $\int \dfrac{1}{x^{\pi}} \phantom{x}dx = \dfrac{x^{1 – \pi}}{1 – \pi} + C$

2.
a. $\int -6x^5 \phantom{x}dx = – x^6+C$
b. $\int \dfrac{1}{3x^4} \phantom{x}dx = -\dfrac{1}{9x^3}+C$
c. $\int (3x^4 – 6x^2 + 12) \phantom{x}dx=\dfrac{3x^5}{5} – 2x^3 +12x +C$
d. $\int (\dfrac{1}{x} – \sec^2 x) \phantom{x}dx= \ln |x| – \tan x + C$
3.
a. $\int 6\sqrt{x} – \sqrt[5]{x} \phantom{x}dx = \dfrac{x^4}{4} – \dfrac{3x^2}{2} -\dfrac{1}{2x^2} +C$
b. $\int \dfrac{4x^3 – 5}{x^2} \phantom{x}dx =2x^2+ \dfrac{5}{x}+ C$
c. $\int (3e^x – 8\sec^2 x) \phantom{x}dx = 3e^x- 8\tan \left(x\right) +C$
d. $\int \dfrac{6 – 5x^6 – 2x^3}{x^3} \phantom{x}dx = -\dfrac{3}{x^2}- \dfrac{5x^4}{4}-2x +C$

Images/mathematical drawings are created with GeoGebra.