Arc of a Circle – Explanation & Examples

After the radius and diameter, another important part of a circle is an arc. In this article, we will discuss what an arc is, find the length of an arc, and measure an arc length in radians. We will also study the minor arc and major arc.

What is an Arc of a Circle?

An arc of a circle is any portion of the circumference of a circle. To recall, the circumference of a circle is the perimeter or distance around a circle. Therefore, we can say that the circumference of a circle is the full arc of the circle itself.

How to Find the Length of an Arc?

The formula for calculating the arc states that:

Arc length = 2πr (θ/360)

Where r = the radius of the circle,

π = pi = 3.14

θ = the angle (in degrees) subtended by an arc at the center of the circle.

360 = the angle of one complete rotation.

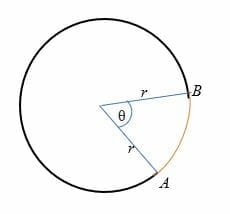
From the above illustration, the length of the arc (drawn in red) is the distance from point A to point B.

Let’s work out a few example problems about the length of an arc:

Example 1

Given that arc, AB subtends an angle of 40 degrees to the center of a circle whose radius is 7 cm. Calculate the length of arc AB.

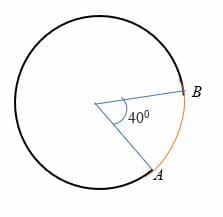
Solution

Given r = 7 cm

θ = 40 degrees.

By substitution,

The length of an arc = 2πr(θ/360)

Length = 2 x 3.14 x 7 x 40/360

= 4.884 cm.

Example 2

Find the length of an arc of a circle that subtends an angle of 120 degrees to the center of a circle with 24 cm.

Solution

The length of an arc = 2πr(θ/360)

= 2 x 3.14 x 24 x 120/360

= 50.24 cm.

Example 3

The length of an arc is 35 m. If the radius of the circle is 14 m, find the angle subtended by the arc.

Solution

The length of an arc = 2πr(θ/360)

35 m = 2 x 3.14 x 14 x (θ/360)

35 = 87.92θ/360

Multiply both sides by 360 to remove the fraction.

12600 = 87.92θ

Divide both sides by 87.92

θ = 143.3 degrees.

Example 4

Find the radius of an arc that is 156 cm in length and subtends an angle of 150 degrees to the circle’s center.

Solution

The length of an arc = 2πr(θ/360)

156 cm = 2 x 3.14 x r x 150/360

156 = 2.6167 r

Divide both sides by 2.6167

r = 59.62 cm.

So, the radius of the arc is 59.62 cm.

How to Find the Arc Length in Radians?

There is a relationship between the angle subtended by an arc in radians and the ratio of the length of the arc to the radius of the circle. In this case,

θ = (the length of an arc) / (the radius of the circle).

Therefore, the length of the arc in radians is given by,

S = r θ

where, θ = angle subtended by an arc in radians

S = length of the arc.

r = radius of the circle.

One radian is the central angle subtended by an arc length of one radius, i.e., s = r

The radian is just another way of measuring the size of an angle. For instance, to convert angles from degrees to radians, multiply the angle (in degrees) by π/180.

Similarly, to convert radians to degrees, multiply the angle (in radians) by 180/π.

Example 5

Find the length of an arc whose radius is 10 cm and the angle subtended is 0.349 radians.

Solution

Arc length = r θ

= 0.349 x 10

= 3.49 cm.

Example 6

Find the length of an arc in radians with a radius of 10 m and an angle of 2.356 radians.

Solution

Arc length = r θ

= 10 m x 2.356

= 23.56 m.

Example 7

Find the angle subtended by an arc with a length of 10.05 mm and a radius of 8 mm.

Solution

Arc length = r θ

10.05 = 8 θ

Divide both sides by 8.

1.2567 = θ

There, the angle subtended by the arc is 1.2567 radians.

Example 8

Calculate the radius of a circle whose arc length is 144 yards and arc angle is 3.665 radians.

Solution

Arc length = r θ

144 = 3.665r

Divide both sides by 3.665.

144/3.665 = r

r = 39.29 yards.

Example 9

Calculate the length of an arc which subtends an angle of 6.283 radians to the center of a circle which has a radius of 28 cm.

Solution

Arc length = r θ

= 28 x 6.283

= 175.93 cm

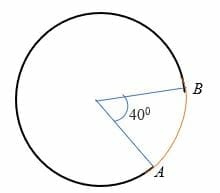
Minor arc (h3)

The minor arc is an arc that subtends an angle of less than 180 degrees to the circle’s center. In other words, the minor arc measures less than a semicircle and is represented on the circle by two points. For example, arc AB in the circle below is the minor arc.

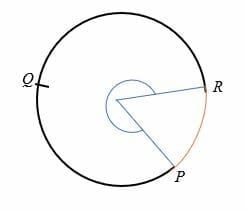
Major arc (h3)

The major arc of a circle is an arc that subtends an angle of more than 180 degrees to the circle’s center. The major arc is greater than the semi-circle and is represented by three points on a circle.

For example, PQR is the major arc of the circle shown below.