- Home
- >
- Area Between Two Curves – Definition, Process, and Examples
JUMP TO TOPIC
Area Between Two Curves – Definition, Process, and Examples
Through integral calculus, we can now calculate the area found between two curves. When given two functions, it’s now possible for us to calculate the area formed by their curves at a given interval. Learning how to find the area between two curves is a fundamental process that has numerous applications in mathematics, finance, and other STEM fields.
Finding the area between two curves is a direct application of definite integrals. When given two functions, the area between two curves can be calculated by subtracting the lower curve from the upper curve (or the leftmost curve from the rightmost) then evaluating the definite integral of the function.
In this article, we’ll focus on highlighting the process of finding the areas between curves using our knowledge of integral calculus. We’ve learned about finding the area under a curve in the past, so make sure you are familiar with this process and this will guarantee you to master our current topic much faster.
What is the area between two curves?
The area between two curves is geometrically the area bounded by their graphs within the given interval. When given two functions, $f(x)$ and $g(x)$, that are continuous through the interval, $[a, b]$, we can use this definition to find the area between them.
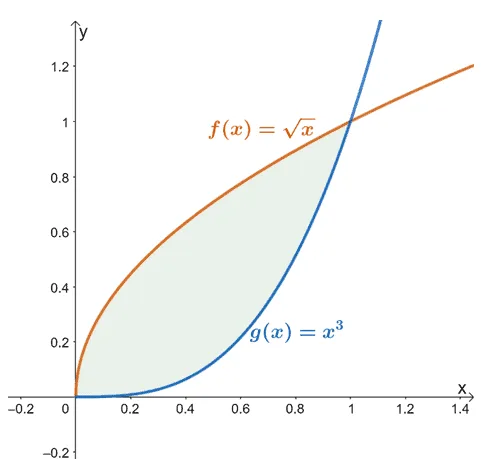
For example, when we have $f(x) = \sqrt{x}$ and $g(x) = x^3$, the area found between the two functions from $x =0$ to $x =1$ is represented by the shaded region (in green) shown above.
Area between two curves definition
Finding the area between two curves is an extension of finding the area under the function’s curve. The image below shows how the value of the area between the two curves is equivalent to the difference between the areas under each curve.
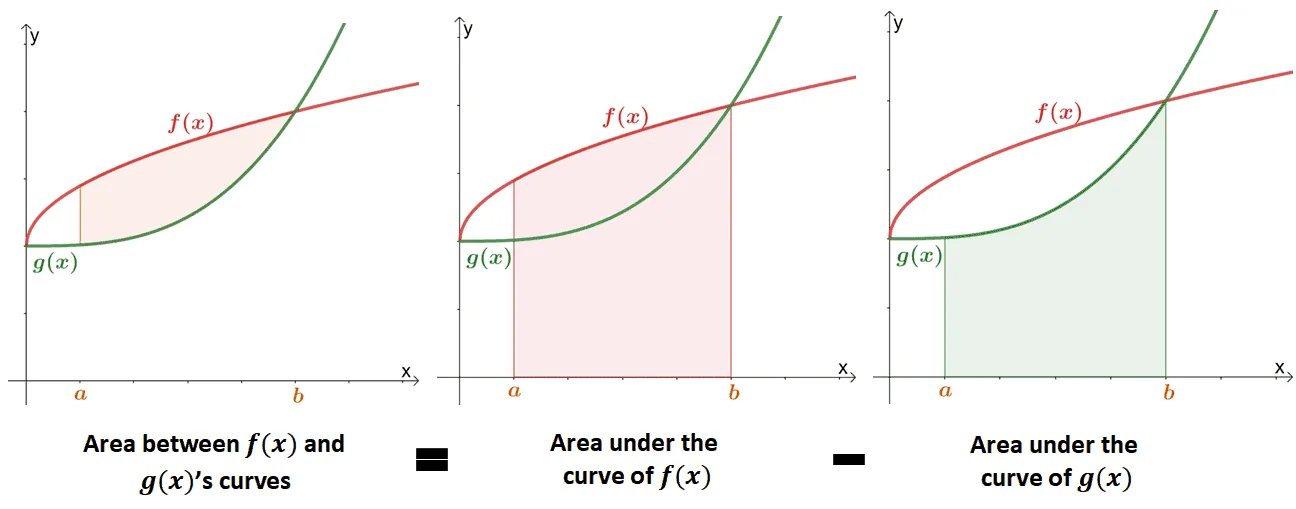
In the past, we’ve learned that the area under the curve can be approximated using definite integrals or the Riemann sum. We can use the formal definition of an area under the curve to mathematically define the area between two curves.
Let’s say we have two continuous functions, $f(x)$ and $g(x)$, over the interval, $[a, b]$. The area between two curves can be defined through the Riemann sum and definite integral expressions shown below where $A$ represents the area between two curves.
Riemann Sum | Definite Integral |
\begin{aligned}A&= \lim_{n \rightarrow \infty} \sum_{i = 1}^{n} [f(x_i) – g(x_i)]\Delta x_i\\&= \lim_{n \rightarrow \infty}\left[\sum_{i = 1}^{n} f(x_i)\Delta x_i – \sum_{i = 1}^{n} g(x_i)\Delta x_i \right ] \end{aligned} | \begin{aligned}A &= \int_{a}^{b} f(x)\phantom{x}dx – \int_{a}^{b}g(x) \phantom{x}dx\\ &= \int_{a}^{b} [f(x) – g(x)]\phantom{x}dx\end{aligned} |
These two formulas confirm that the areas between two curves are related to areas under the curve. For example, the functions $f(x)$ and $g(x)$ are continuous over the interval, $[a, b]$. When $g(x) \leq f(x)$ for all $x$ within the given interval, we have the area between the curves of $f(x)$ and $g(x)$:
\begin{aligned}A &= \int_{a}^{b} [f(x) – g(x)] \phantom{x}dx\end{aligned}
This means that the area between the curves bounded by the graph of $\boldsymbol{f(x)}$ and $\boldsymbol{g(x)}$ and the vertical lines formed by $\boldsymbol{x = a}$ and $\boldsymbol{x = b}$ is equivalent to the difference between the areas under the curves.
There are instances, however, that it’s difficult to determine which of the two given functions is positioned directly above the other. There are also times when we’re given the boundaries and curve’s expressions with respect to $y$.
When any of this case happens, we can instead observe the positions of the curve with respect to the $\boldsymbol{y}$-axis.
\begin{aligned}A&= \int_{a}^{b} f(y) – g(y) \phantom{x}dy\end{aligned}
For this equation, $\boldsymbol{f(y)}$ is the right-most curve and $\boldsymbol{[a, b]}$ are the horizontal bounds. This means that we can also define areas between two curves based on their positioning from left to right.
In the past, we’ve learned that the area under the curve can be approximated using definite integrals or the Riemann sum. We can use the formal definition of an area under the curve to mathematically define the area between two curves.
Let’s say we have two continuous functions, $f(x)$ and $g(x)$, over the interval, $[a, b]$. The area between two curves can be defined through the Riemann sum and definite integral expressions shown below where $A$ represents the area between two curves.
Riemann Sum | Definite Integral |
\begin{aligned}A&= \lim_{n \rightarrow \infty} \sum_{i = 1}^{n} [f(x_i) – g(x_i)]\Delta x_i\\&= \lim_{n \rightarrow \infty}\left[\sum_{i = 1}^{n} f(x_i)\Delta x_i – \sum_{i = 1}^{n} g(x_i)\Delta x_i \right ] \end{aligned} | \begin{aligned}A &= \int_{a}^{b} f(x)\phantom{x}dx – \int_{a}^{b}g(x) \phantom{x}dx\\ &= \int_{a}^{b} [f(x) – g(x)]\phantom{x}dx\end{aligned} |
These two formulas confirm that the areas between two curves are related to areas under the curve. For example, the functions $f(x)$ and $g(x)$ are continuous over the interval, $[a, b]$. When $g(x) \leq f(x)$ for all $x$ within the given interval, we have the area between the curves of $f(x)$ and $g(x)$:
\begin{aligned}A &= \int_{a}^{b} [f(x) – g(x)] \phantom{x}dx\end{aligned}
This means that the area between the curves bounded by the graph of $\boldsymbol{f(x)}$ and $\boldsymbol{g(x)}$ and the vertical lines formed by $\boldsymbol{x = a}$ and $\boldsymbol{x = b}$ is equivalent to the difference between the areas under the curves.
There are instances, however, that it’s difficult to determine which of the two given functions is positioned directly above the other. There are also times when we’re given the boundaries and curve’s expressions with respect to $y$.
When any of this case happens, we can instead observe the positions of the curve with respect to the $\boldsymbol{y}$-axis.
\begin{aligned}A&= \int_{a}^{b} f(y) – g(y) \phantom{x}dy\end{aligned}
For this equation, $\boldsymbol{f(y)}$ is the right-most curve and $\boldsymbol{[a, b]}$ are the horizontal bounds. This means that we can also define areas between two curves based on their positioning from left to right.
How to find the area between two curves?
As discussed in the earlier section, we can determine the area between the curves of two functions using their definite integrals. Use these steps below as a guide when calculating the area between two curves, $f(x)$ and $g(x)$:
- When it’s not given yet, find the two vertical bounds of the two functions by equating the two functions and solving for $x$.
- Identify which of the function is positioned higher than the other over the interval, $[a, b]$. Graph the functions when you have to.
- Label the higher function as $f(x)$ and the lower function as $g(x)$. This is an optional step but extremely helpful when you’re still mastering this topic.
- Simplify the expression of $f(x) – g(x)$ then evaluate the definite integral, $\int_{a}^{b} [f(x) – g(x)]\phantom{x} dx$.
The best way to familiarize yourself with the steps is by practice. Of course, as with areas under the curve, when the returned value is negative, finalize the area by taking its absolute value.
Let’s begin by calculating the area of the region bounded by the curves of $y = x^2$ and $y = -x^2 + 4x$. Since the interval is still not given, let’s equate the two equations to find the intervals enclosing the region.
\begin{aligned}x^2 &= -x^2 + 4x\\ 2x^2 – 4x&= 0\\2x(x -2)&= 0\\\\x&=0, 2\end{aligned}
This means that the we’re calculating the area of the region from the interval, $[0, 2]$. Substitute $x =0$ and $x=2$ into the values of either $y = x^2$ or $y = -x^2 + 4x$ to find the curves’ points of intersection.
\begin{aligned}\boldsymbol{x}\end{aligned} | \begin{aligned}\boldsymbol{y}\end{aligned} | \begin{aligned}\boldsymbol{(x, y)}\end{aligned} |
\begin{aligned}x &= 0\end{aligned} | \begin{aligned}y &= 0^2\\&= 0\end{aligned} | \begin{aligned}(0, 0)\end{aligned} |
\begin{aligned}x &= 2\end{aligned} | \begin{aligned}y &= 2^2\\&= 4\end{aligned} | \begin{aligned}(2, 4)\end{aligned} |
Let us show you the graph of the curves on one $xy$-coordinate system then highlight the area of the region enclosed by the two functions.
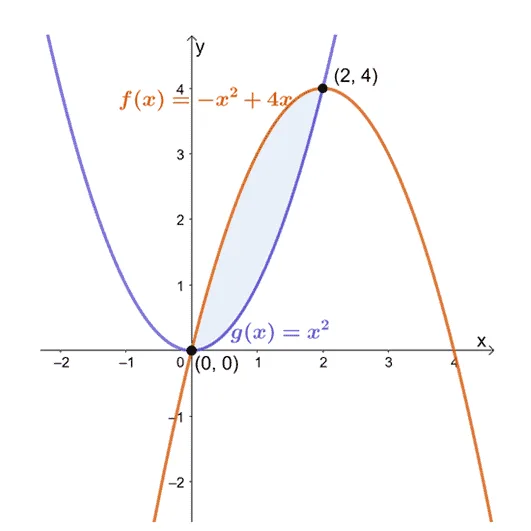
The image shows us that the function $y = -x^2 + 4x$ lies above the curve of $y = x^2$ from $x=0$ to $x =2$. Hence, we’ll use $f(x) = -x^2 + 4x$ and $g(x) = x^2$ when calculating for the area between these two curves.
\begin{aligned}A &= \int_{0}^{2} [f(x) – g(x)] \phantom{x}dx\\&= \int_{0}^{2} (-x^2 + 4x – x^2) \phantom{x}dx\\ &= \int_{0}^{2} (-2x^2 + 4x) \phantom{x}dx\\ &=\int_{0}^{2} -2(x^2 – 2x) \phantom{x}dx \end{aligned}
Now that we have a definite integral expression representing the areas between the two curves. Apply integral properties and antiderivative formulas to evaluate the definite integral. Here are some tips to follow if you want to try evaluating the definite integral first:
- Factor out $-2$ from the integral expression using the constant multiple property, $\int_{a}^{b} k f(x) \phantom{x}dx = k\int_{a}^{b} f(x) \phantom{x}dx$.
- Distribute the integral operation using the difference property of definite integrals, $\int_{a}^{b} [f(x) –g(x)]\phantom{x}dx = \int_{a}^{b} f(x)\phantom{x}dx – \int_{a}^{b} g(x)\phantom{x}dx$.
- Apply the power rule,$\int x^n \phantom{x}dx = \dfrac{x^{n +1}}{n + 1} + C$, to integrate each term.
\begin{aligned}\int_{0}^{2} -2(x^2 – 2x) \phantom{x}dx &= -2\int_{0}^{2} (x^2 – 2x) \phantom{x}dx \\&= -2 \left[\int_{0}^{2}x^2\phantom{x}dx – \int_{0}^{2}2x \phantom{x}dx \right ]\\&= -2\left[\int_{0}^{2}x^2\phantom{x}dx – 2\int_{0}^{2}x \phantom{x}dx \right ]\\&= -2\left[\left(\dfrac{x^{2 + 1}}{2 + 1} \right )- 2\left(\dfrac{x^{1 + 1}}{1 + 1} \right )\right ]_{0}^{2}\\&=-2\left[\dfrac{x^3}{3} – \dfrac{x^2}{2}\right ]_{0}^{2} \\&= -2 \left[\left(\dfrac{2^3}{3} – \dfrac{2^2}{2} \right ) – 2\left(\dfrac{0^3}{3} – \dfrac{0^2}{2} \right ) \right ]\\&= -2 \cdot \dfrac{2}{3}\\&= -\dfrac{4}{3} \end{aligned}
Since $A$ is negative, simply take the absolute value of the resulting expression. This means that the area of the region between the two functions, $y = x^2$ and $y = -x^2 + 4x$, is equal to $\dfrac{4}{3}$ squared units from $x = 0$ to $x =2$.
Let’s now try finding the area between the curves with respect to the vertical axis: $g(y) = 1 – y^2$ and $f(y) = y^2 -1$ enclosed from $y =-1$ to $ y=1$.
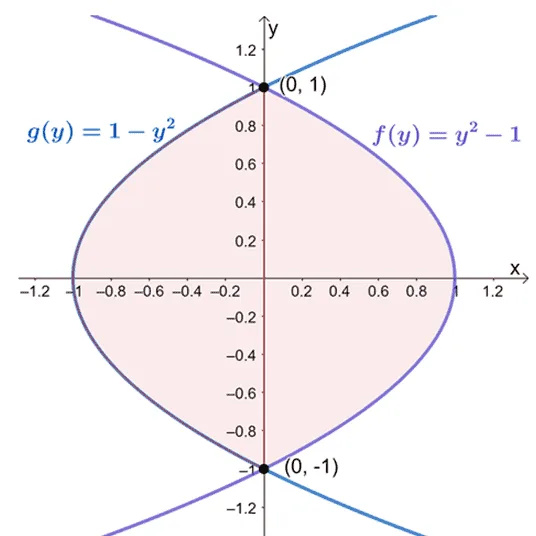
When this happens, we simply subtract the left-most function from the right-most function then evaluate the definite integral from $y= -1$ to $y =1$.
\begin{aligned}\int_{-1}^{1} [f(y) -g(y)]\phantom{x}dy &= \int_{-1}^{1} [(y^2 -1) -(1- y^2)]\phantom{x}dy\\ &= \int_{-1}^{1} (y^2 -1 -1 + y^2) \phantom{x}dy\\&= \int_{-1}^{1}2y^2 -2 \phantom{x}dy\end{aligned}
Evaluate the definite integral using antiderivative formulas and properties we’ve learned in the past. The only difference is that we’re using the variable, $y$.
\begin{aligned}\int_{-1}^{1}2y^2 -2 \phantom{x}dy &= 2\int_{-1}^{1} (y^2 – 1)\phantom{x}dy\\&= 2\left[\int_{-1}^{1} y^2\phantom{x}dy – \int_{-1}^{1}1\phantom{x}dy \right ]\\&= 2\left[\dfrac{y^{2 + 1}}{2 + 1} – y\right ]_{-1}^{1}\\&= 2\left[\dfrac{y^3}{3} -y \right ]_{-1}^{1}\\&= 2\left[\left(\dfrac{1^3}{3} – 1 \right ) -\left(\dfrac{(-1)^3}{3} – (-1) \right ) \right ]\\&= 2\left(-\dfrac{4}{3} \right )\\&= -\dfrac{8}{3}\end{aligned}
Take the absolute value of the result to return the area between the two curves. Hence, we’ve shown that the area between $g(y) = 1 – y^2$ and $f(y) = y^2 -1$ is equal to $\dfrac{8}{3}$ squared units.
In the next section, we’ll show you more examples with different cases and functions to help you master this topic. These examples will also be a great avenue for you to refresh your skills in evaluating integrals, in general.
Example 1
Find the area bounded by the following curves: $y = 2x + 1$, $y = 4 – x$, $x = 1$, and $x =4$.
Solution
Graph the two curves by finding the corresponding ordered pairs when we substitute $x= 0$ and $x =4$ into each expression.
\begin{aligned}\boldsymbol{x}\end{aligned} | \begin{aligned}\boldsymbol{y}\end{aligned} | \begin{aligned}\boldsymbol{(x, y)}\end{aligned} | |
\begin{aligned}y &= 2x +1\end{aligned} | \begin{aligned}x &= 1\end{aligned} | \begin{aligned}y &= 2(1) +1\\&= 3\end{aligned} | \begin{aligned}(1, 3)\end{aligned} |
\begin{aligned}x &= 4\end{aligned} | \begin{aligned}y &= 2(4) + 1\\&= 9\end{aligned} | \begin{aligned}(4, 9)\end{aligned} | |
\begin{aligned}y &= 4 -x\end{aligned} | \begin{aligned}x &= 1\end{aligned} | \begin{aligned}y &= 4 – 1\\&= 3\end{aligned} | \begin{aligned}(1, 3)\end{aligned} |
\begin{aligned}x &= 4\end{aligned} | \begin{aligned}y &= 4 – 4\\&= 0\end{aligned} | \begin{aligned}(4, 0)\end{aligned} |
Use these ordered pairs as a guide when graphing the graph. Use the curve of the functions to help you identify which curve is lying on top of the other over the interval, $[1, 4]$.
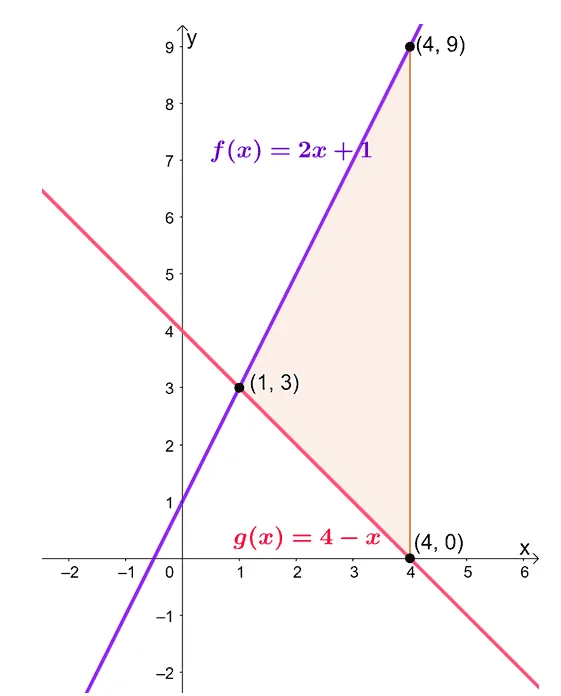
This means that we can calculate the area between the two curves by evaluating the definite integral, $\int_{1}^{4} [f(x) – g(x)]\phantom{x}dx$.
\begin{aligned}\int_{1}^{4} [f(x) – g(x)]\phantom{x}dx &= \int_{1}^{4} [(2x + 1) – (4 -x)]\phantom{x}dx \\&= \int_{1}^{4} (2x + 1 – 4 +x)\phantom{x}dx\\&= \int_{1}^{4} (3x – 3)\phantom{x}dx\\&= \int_{1}^{4} 3(x – 1)\phantom{x}dx\end{aligned}
Apply antiderivative formulas and properties to evaluate $\int_{1}^{4} (3x – 3)\phantom{x}dx$.
- Factor out $3$ from the definite integral.
- Distribute the integral operation to each term.
- Apply the power rule, $\int x^n \phantom{x}dx = \dfrac{x^{n + 1}}{n + 1} + C$, and the constant rule, $\int k \phantom{x} dx = kx + C$, to integrate the resulting expression.
\begin{aligned}\int_{1}^{4} 3(x – 1)\phantom{x}dx &= 3\int_{1}^{4} (x – 1)\phantom{x}dx\\ &= 3\left[\int_{1}^{4} x \phantom{x}dx – \int_{1}^{4} 1\phantom{x}dx \right ]\\&= 3\left[ \dfrac{x^2}{2} – x \right ]_{1}^{4}\\&= 3\left[\left(\dfrac{4^2}{2} – 4 \right )- \left(\dfrac{1^2}{2} – 1 \right ) \right ]\\&= 3\left(4 + \dfrac{1}{2} \right )\\ &= \dfrac{27}{2}\end{aligned}
Hence, the area enclosed by the curves of $y =2x + 1$ and $y = 4 -x$ from $x= 1$ to $x =4$ is equal to $13.5$ squared units.
Example 2
What is the area of the region enclosed between the graphs of $y = 16 – \left(\dfrac{x}{2}\right)^2$ and $y = 8 – x$?
Solution
Let’s first determine the points of intersections shared between the two curves. Equate the two expressions then solve for $x$. The values of $x$ will define our bounds for the area of the region.
\begin{aligned}16 – \left(\dfrac{x}{2}\right)^2 &= 8 – x\\16 – \dfrac{x^2}{4} &= 8 -x\\64 – x^2 &= 32 – 4x\\x^2 -4x – 32&= 0\\(x + 4)(x -8) &= 0\\x&= -4, 8\end{aligned}
Graph the two curves to determine the positions of the two curves within the interval, $[-4, 8]$.
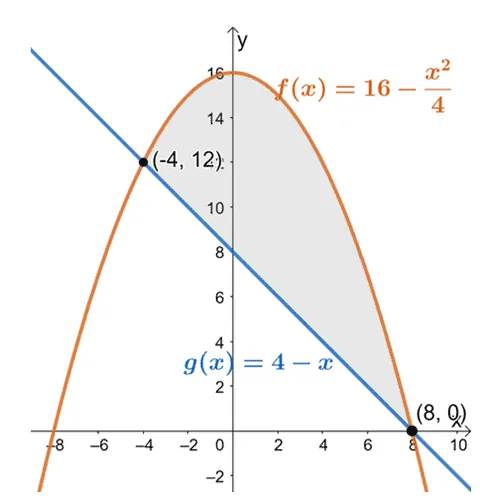
From this, we can see that the graph of $f(x) = 16 – \dfrac{x^2}{4}$ is lying above the linear function, $g(x) = 4 –x$, for the interval, $[-4, 8]$. To find the area of the enclosed region, we simply evaluate the definite integral of their difference and over the given interval:$[-4, 8]$.
\begin{aligned} A &= \int_{-4}^{8} [f(x) – g(x)]\phantom{x} dx\\&= \int_{-4}^{8}\left[\left(16 – \dfrac{x^2}{4}\right) – (4 -x) \right ] \phantom{x}dx\\&= \int_{-4}^{8} \left(12 – \dfrac{x^2}{4} + x \right ) \phantom{x}dx\\&= \int_{-4}^{8} \left(- \dfrac{x^2}{4} + x +12\right ) \phantom{x}dx\end{aligned}
Distribute the definite integral operation to each of the term. Apply the power rule as well as the constant property to evaluate the definite integral completely.
\begin{aligned} \int_{-4}^{8} \left(- \dfrac{x^2}{4} + x +12\right ) \phantom{x}dx &=\int_{-4}^{8} -\dfrac{x^2}{4} \phantom{x}dx + \int_{-4}^{8} x \phantom{x}dx + \int_{-4}^{8} 12\phantom{x}dx\\ &= -\dfrac{1}{4}\int_{-4}^{8} x^2 \phantom{x}dx + \int_{-4}^{8} x \phantom{x}dx + \int_{-4}^{8} 12\phantom{x}dx\\&= -\dfrac{1}{4}\left[\dfrac{x^3}{3} \right ]_{-4}^{8} + \left[\dfrac{x^2}{2} \right ]_{-4}^{8} + \left[12x\right ]_{-4}^{8} \\&= -\dfrac{1}{4}\left[\dfrac{(8)^3}{3} -\dfrac{(-4)^3}{3} \right ] + \left[\dfrac{(8)^2}{2} -\dfrac{(-4)^2}{2} \right ] + [12(8) -12(-4)]\\ &= -48 + 24 + 144\\&= 120\end{aligned}
This means that the area enclosed by the two curves, $y = 16 – \left(\dfrac{x}{2}\right)^2$ and $y = 8 – x$, is equal to $120$ squared units.
Example 3
What is the area of the region enclosed between the graphs of $y = \cos x$ and $y = \sin x$ over the interval of $\left[0, \dfrac{\pi}{2}\right]$?
Solution
First, graph the curves of $y = \sin x $ and $y = \cos x$ from $x = 0$ and $x = \pi$. Take note that $\sin x$ will only be equal to $\cos x$ when $x = \dfrac{\pi}{4}$, so the two curves are expected to intersect at $x = \dfrac{\pi}{4}$.
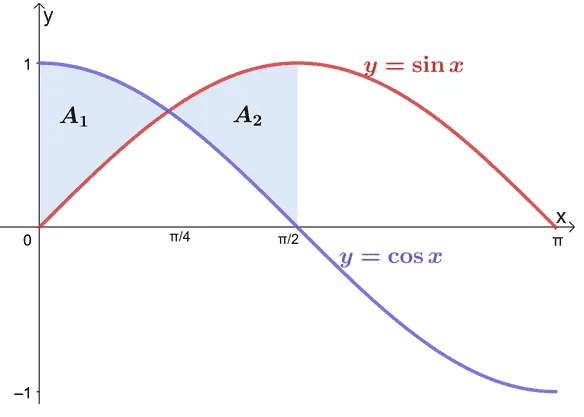
From the graph, we can see that the curve of $y = \cos x$ is lying above the curve of $y = \sin x$ from $x =0$ to $x = \dfrac{\pi}{4}$. On the other hand, $y = \sin x$’s curve lies above the $y = \cos x$’s curve from $x = \dfrac{\pi}{4}$ to $x = \dfrac{\pi}{2}$. This means that the expression between those two sets of intervals will not be the same, so let’s break down the region’s area into two smaller regions: $A_1$ and $A_2$.
\begin{aligned} A&= A_1 + A_2\\A_1 &= \int_{0}^{\pi/4} (\cos x – \sin x) \phantom{x}dx\\ A_2 &= \int_{\pi/4}^{\pi/2} (\sin x – \cos x) \phantom{x}dx\end{aligned}
Evaluate the two definite integrals separately first using the two antiderivative formulas shown below:
- $\int \sin x \phantom{x}dx = – \cos x + C$
- $\int \cos x \phantom{x}dx = \sin x + C$
\begin{aligned}\boldsymbol{A_1}\end{aligned} | \begin{aligned}\int_{0}^{\pi/4} (\cos x – \sin x) \phantom{x}dx &= \int_{0}^{\pi/4} \cos x\phantom{x}dx – \int_{0}^{\pi/4} \sin x \phantom{x}dx\\&= [\sin x]_{0}^{\pi/4} – [-\cos x]_{0}^{\pi/4}\\&=\left(\sin \dfrac{\pi}{4} – \sin 0 \right ) – \left(-\cos \dfrac{\pi}{4} – -\cos0 \right )\\&= \left(\dfrac{\sqrt{2}}{2} – 0 \right ) -\left(-\dfrac{\sqrt{2}}{2}+ 1\right )\\&= \sqrt{2} -1 \end{aligned} |
\begin{aligned}\boldsymbol{A_2}\end{aligned} | \begin{aligned}\int_{\pi/4}^{\pi/2} (\sin x – \cos x) \phantom{x}dx &= \int_{\pi/4}^{\pi/2} \sin x\phantom{x}dx – \int_{\pi/4}^{\pi/2} \cos x \phantom{x}dx\\&= [-\cos x]_{\pi/4}^{\pi/2} – [\sin x]_{\pi/4}^{\pi/2}\\&=\left(-\cos \dfrac{\pi}{2} – -\cos \dfrac{\pi}{4} \right ) – \left(\sin \dfrac{\pi}{2} – \sin \dfrac{\pi}{4} \right )\\&= \left(0 + \dfrac{\sqrt{2}}{2}\right) – \left(1 – \dfrac{\sqrt{2}}{2}\right)\\&= \sqrt{2} -1 \end{aligned} |
Find the total area of the enclosed region by adding the absolute values of $A_1$ and $A_2$.
\begin{aligned}A &= A_1 + A_2\\&= (\sqrt{2} -1) + (\sqrt{2} -1)\\&= 2\sqrt{2} -2\end{aligned}
This means that the area of the enclosed region formed by $y = \cos x$ and $y = \sin x$ over the interval, $\left[0, \dfrac{\pi}{2}\right], is $2\sqrt{2} -1 \approx 0.828$ squared units.
Example 4
What is the area of the region enclosed between the curves of $x = y^2 -4y$ and $x = -y^2 + 2y$?
Solution
Notice how the function is now in terms of $y$? This time, we’ll find the area of the enclosed region with respect to the upper and lower boundaries. Find the points of intersection by equating the two curves’ expressions in terms of $y$.
\begin{aligned}y^2 – 4y&= -y^2 + 2y\\ 2y^2 – 6y&= 0\\ 2y(y – 3) &= 0\\y &= 0, 3\end{aligned}
This means that we want to evaluate the definite integral, $\int_{a}^{b}[f(y)-g(y)]\phantom{x} dy$, when $a = 0$ and $b = 3$.
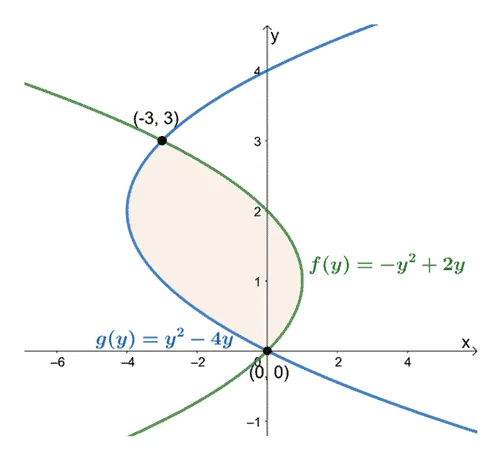
Observing their positions from $y =0$ to $y =3$, subtract the leftmost curve’s expression from the rightmost curve’s expression. The area of the enclosed region is equal to the definite integral of the resulting expression and evaluated over the interval, $[0, 3]$.
\begin{aligned}A &= \int_{0}^{3} [f(y) – g(y)] \phantom{x} dy\\&= \int_{0}^{3} [(-y^2 + 2y) – (y^2 – 4y)]\phantom{x} dy\\&= \int_{0}^{3}(-2y^2 + 6y) \phantom{x}dy\\ &=\int_{0}^{3} -2(y^2 -3y)\phantom{x}dy\end{aligned}
Evaluate the definite integral of the resulting expression. Use the pointers below as a guide in integrating the expression.
- Factor out $-2$ from the definite integral.
- Distribute the definite integral operation.
- Apply the power rule to integrate the expression completely.
\begin{aligned}\int_{0}^{3} -2(y^2 -3y)\phantom{x}dy &= -2\int_{0}^{3} (y^2 -3y)\phantom{x}dy \\&= -2\left[\int_{0}^{3}y^2 \phantom{x}dy – \int_{0}^{3}3y \phantom{x}dy \right ]\\&=-2\left[\int_{0}^{3}y^2 \phantom{x}dy – 3\int_{0}^{3}y \phantom{x}dy \right ]\\&= -2\left\{\left[\dfrac{y^3}{3} \right ]_{0}^{3} -3\left[\dfrac{y^2}{2} \right ]_{0}^{3} \right\} \\&= -2\left[\left(\dfrac{3^3}{3} – 0 \right ) – 3\left(\dfrac{3^2}{2} – 0 \right )\right]\\&= -9\end{aligned}
Since areas will always be positive, take the absolute value of the evaluated definite integral to return the area of the enclosed region. This means that the area of the region between the curves of $x = y^2 -4y$ and $x = -y^2 + 2y$ is equal to $9$ squared units.
Practice Questions
1. Find the area bounded by the following curves: $y = -3x + 4$, $y = 6 – x$, $x = 2$, and $x =10$.
2. What is the area enclosed between the graphs of $y = 25 – \left(\dfrac{x}{2}\right)^2$ and $y = 10 – x$?
3. What is the area of the region enclosed between the graphs of $y = \cos x$ and $y = \sin x$ over the interval of $\left[0, \pi\right]$?
4. What is the area of the region enclosed between the graphs of $y = \sin 2x$ and $y = \cos x$ over the interval of $\left[-\dfrac{\pi}{3}, \dfrac{\pi}{3}\right]$?
5. Find the area bounded by the following curves of $x = 6 – 3y^2$ and $x = -3 – y^2$.
Answer Key
1. The area of the enclosed region is $112$ squared units.
2. The area of the enclosed is $\dfrac{512}{3}$ squared units.
3. The area of the enclosed is $2\sqrt{2} \approx 2.828$ squared units.
4. The area of the enclosed is $2$ squared units.
5. The area of the enclosed is $81$ squared units.
Images/mathematical drawings are created with GeoGebra.
