Area of Rhombus – Explanation & Examples

We saw in the Polygon article that the rhombus is a quadrilateral with four parallel sides of equal lengths. The opposite angles of a rhombus are also equal.

Similarly, the diagonals of a rhombus intersect at right angles, and their lengths are always equal. A square is a type of rhombus whose 4 angles are all right angles. Sometimes, a rhombus is referred to as a rhomb, diamond, or lozenge.

In this article, you will learn how to calculate a rhombus area using the three areas of rhombus formulas.

How to Calculate the Area of a Rhombus?

The area of a rhombus is the region enclosed by the 4 sides of a rhombus.

There are three ways to find the area of a rhombus.

One way is by the use of the altitude and side of a rhombus. The second method entails using the side and angle, and the last method entails using the diagonals.

These formulas for calculating the area of a rhombus are collectively known as rhombus area formulas. Let’s take a look.

Rhombus Area Formula

We can find the area of the rhombus in multiple ways. We will saw each of them one by one below.

Area of Rhombus using Altitude and Base

When the altitude or height and the length of the sides of a rhombus are known, the area is given by the formula;

Area of rhombus = base × height

A = b × h

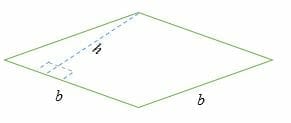
Let us see understand this through an example:

Example 1

Find the area of a rhombus whose side is 30 cm and height is 15 cm.

Solution

A = b × h

= (30 x 15) cm²

= 450 cm²

Therefore, the area of the rhombus is 450 cm².

Example 2

Calculate the area of the rhombus shown below.

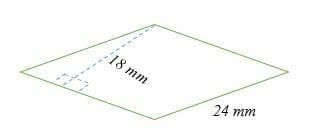
Solution

A = b × h

= (18 x 24) mm²

Example 3

If the height and area of a rhombus are 8 cm and 72 cm^2, respectively, find the rhombus’s dimensions.

Solution

A = b × h

72 cm² = 8 cm x b

Divide both sides by 8.

72 cm²/8 cm = b

b = 9 cm.

Therefore, the dimensions of the rhombus are 9 cm by 9 cm.

Example 4

The base of a rhombus is 3 times plus 1 more than the height. If the area of the rhombus is 10 m², find the base and height of the rhombus.

Solution

Let the height of rhombus = x

and base = 3x + 1

A = b × h

10 m² = x (3x + 1)

10 = 3x² + x

3x² + x – 10 = 0

Solve the quadratic equation.

⟹ 3x² + x – 10 = 3x² + 6x – 5x – 10

⟹ 3x (x + 2) – 5(x + 2)

⟹ (3x – 5) (x + 2) = 0

⟹ 3x – 5 = 0

⟹ x = 5/3

⟹ x + 2= 0

x = -2

Now substitute the value of x.

Height = x = 5/3 m

Base = 3x + 1 = 3(5/3) + 1 = 6 m

So, the base of the rhombus is 6 m, and the height is 5/3 m.

Area of Rhombus Using Diagonals

Given the lengths of the diagonals, the area of a rhombus is equal to half the diagonals’ product.

A = ½ × d₁ × d₂

Where d₁ and d₂ are the diagonals of a rhombus.

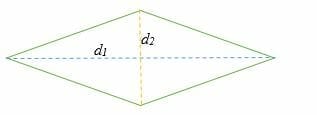
Example 5

The two diagonals of a rhombus are 12 cm and 8 cm. Calculate the rhombus area.

Solution:

Let d₁ = 12 cm and d₂ = 8 cm.

A = ½ × d₁ × d₂

= (½ × 12 × 8) cm².

= 48 cm².

Example 6

Calculate the side lengths if its area is 24 cm², diagonal is 8 cm, and height 3 cm.

Solution

Let d₁ = 8 cm.

d₂ =?

A = ½ × d₁ × d₂

24 cm² = ½ × 8 × d₂

24 cm² = 4d₂

Divide both sides by 4 to get,

6 = d₂

Therefore, the other diagonal is 6 cm.

Now, calculate the side lengths of the rhombus.

A = b × h

24 cm² = 3 cm x b

Divide both sides by 3.

8 cm = b.

Therefore, the side lengths of the rhombus are 8 cm.

Example 7

Find the diagonals of the rhombus shown below if its area is 3,458 cm².

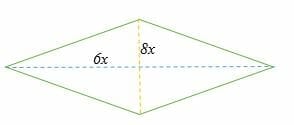
Solution

A = ½ × d₁ × d₂

3,458 cm² = ½ * 6x * 8x

3,458 cm² = 24x²

Divide both sides by 24.

3,458/24 = x²

144 = x²

Find the square root of both sides.

x = -12 or 12.

Length cannot be a negative number; therefore, substitute only x =12 in the diagonals’ equations.

6x = 6 * 12 = 72 cm

8x = 8 * 12 = 96 cm

Hence, the lengths of the diagonals are 72 cm and 96 cm.

Example 8

Suppose the rate of polishing a floor is $ 4 per square meter. Find the cost of polishing a rhombus-shaped floor, and each of its diagonals is 20 m and 12 m.

Solution

To find the cost of polishing the floor, multiply the polishing rate by the area of rhombus shaped floor.

A = ½ × 20 m × 12 m

= 120 m²

Cost of painting = 120 m² x $ 4 per m.

= $480

Area of Rhombus using the Length of the Sides and an included Angle.

The area of a rhombus is equal to the product side length squared and the sine of the angle between the two sides.

Area of rhombus = b² × Sine (A)

Where A = angle formed between two sides of a rhombus.

Example 9

Find the area of a rhombus whose sides are 8 cm, and the angle between the two sides is 60 degrees.

Solution

A = b² × Sine (A)

= 8² x sine (60)

= 55.43 cm².

Practice Questions

1. Find the length of a diagonal of a rhombus if the other diagonal is 5 units long, and the area of a rhombus is 30 square units.
2. A kite has a shorter diagonal of length 16 units, a shorter side of length 10 units, and a longer side of length 17 cm. What is the length of the other diagonal?
3. What area of a rhombus whose side lengths are 18 cm each and one diagonal is 20 cm?