Area of Sector – Explanation & Examples

To recall, a sector is a portion of a circle enclosed between its two radii and the arc adjoining them.

For example, a pizza slice is an example of a sector representing a fraction of the pizza. There are two types of sectors, minor and major sector. A minor sector is less than a semi-circle sector, whereas a major sector is a sector that is greater than a semi-circle.

In this article, you will learn:

• What the area of a sector is.
• How to find the area of a sector; and
• The formula for the area of a sector.

What is the Area of a Sector?

The area of a sector is the region enclosed by the two radii of a circle and the arc. In simple words, the area of a sector is a fraction of the area of the circle.

How to Find the Area of a Sector?

To calculate the area of a sector, you need to know the following two parameters:

• The length of the circle’s radius.
• The measure of the central angle or the length of the arc. The central angle is the angle subtended by an arc of a sector at the center of a circle. The central angle can be given in degrees or radians.

With the above two parameters, finding the area of a circle is as easy as ABCD.  It is just a matter of plugging in the values in the area of the sector formula given below.

Formula for area of a sector

There are three formulas for calculating the area of a sector. Each of these formulas is applied depending on the type of information given about the sector.

Area of a sector when the central angle is given in degrees

If the angle of the sector is given in degrees, then the formula for the area of a sector is given by,

Area of a sector = (θ/360) πr²

A = (θ/360) πr²

Where θ = the central angle in degrees

Pi (π) = 3.14 and r = the radius of a sector.

Area of a sector given the central angle in radians

If the central angle is given in radians, then the formula for calculating the area of a sector is;

Area of a sector = (θr²)/2

Where θ = the measure of the central angle given in radians.

Area of a sector given the arc length

Given the length of the arc, the area of a sector is given by,

Area of a sector = rL/2

Where r = radius of the circle.

L = arc length.

Let’s work out a couple of example problems involving the area of a sector.

Example 1

Calculate the area of the sector shown below.

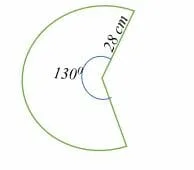
Solution

Area of a sector = (θ/360) πr²

= (130/360) x 3.14 x 28 x 28

= 888.97 cm²

Example 2

Calculate the area of a sector with a radius of 10 yards and an angle of 90 degrees.

Solution

Area of a sector = (θ/360) πr²

A = (90/360) x 3.14 x 10 x 10

= 78.5 sq. yards.

Example 3

Find the radius of a semi-circle with an area of 24 inches squared.

Solution

A semi-circle is the same as half a circle; therefore, the angle θ = 180 degrees.

A= (θ/360) πr²

24 = (180/360) x 3.14 x r²

24 = 1.57r²

Divide both sides by 1.57.

15.287 = r²

Find the square root of both sides.

r = 3.91

So, the radius of the semi-circle is 3.91 inches.

Example 4

Find the central angle of a sector whose radius is 56 cm and the area is 144 cm².

Solution

A= (θ/360) πr²

144 = (θ/360) x 3.14 x 56 x 56.

144 = 27.353 θ

Divide both sides by θ.

θ = 5.26

Thus, the central angle is 5.26 degrees.

Example 5

Find the area of a sector with a radius of 8 m and a central angle of 0.52 radians.

Solution

Here, the central angle is in radians, so we have,

Area of a sector = (θr²)/2

= (0.52 x 8²)/2

= 16.64 m²

Example 6

The area of a sector is 625mm². If the sector’s radius is 18 mm, find the central angle of the sector in radians.

Solution

Area of a sector = (θr²)/2

625 = 18 x 18 x θ/2

625 = 162 θ

Divide both sides by 162.

θ = 3.86 radians.

Example 7

Find the radius of a sector whose area is 47 meters squared and central angle is 0.63 radians.

Solution

Area of a sector = (θr²)/2

47 = 0.63r²/2

Multiply both sides by 2.

94 = 0.63 r²

Divide both sides by 0.63.

r² =149.2

r = 12.22

So, the radius of the sector is 12.22 meters.

Example 8

The length of an arc is 64 cm. Find the area of the sector formed by the arc if the circle’s radius is 13 cm.

Solution

Area of a sector = rL/2

= 64 x 13/2

= 416 cm².

Example 9

Find the area of a sector whose arc is 8 inches and radius is 5 inches.

Solution

Area of a sector = rL/2

= 5 x 8/2

= 40/2

= 20 inches squared.

Example 10

Find the angle of a sector whose arc length is 22 cm and the area is 44 cm².

Solution

Area of a sector = rL/2

44 = 22r/2

88 = 22r

r = 4

Hence, the radius of the sector is 4 cm.

Now calculate the central angle of the sector.

Area of a sector = (θr²)/2

44 = (θ x 4 x 4)/2

44 = 8 θ

θ =5.5 radians.

Therefore, the central angle of the sector is 5.5 radians.