Area of the Shaded Region – Explanation & Examples

The area of the shaded region is most often seen in typical geometry questions. Such questions always have a minimum of two shapes, for which you need to find the area and find the shaded region by subtracting the smaller area from the bigger area.

Or we can say that, to find the area of the shaded region, you have to subtract the area of the unshaded region from the total area of the entire polygon. This depends upon the type of figure given.

In this article, you will learn about:

• What the area of the shaded region is
• How to find the area of a shaded region involving polygons

What is the Area of the Shaded Region?

The area of the shaded region is the difference between the area of the entire polygon and the area of the unshaded part inside the polygon.

The area of the shaded part can occur in two ways in polygons. The shaded region can be located at the center of a polygon or the sides of the polygon.

How to Find the Area of the Shaded Region?

As stated before, the area of the shaded region is calculated by taking the difference between the area of an entire polygon and the area of the unshaded region.

Area of shaded region = area of outer shape – area of the unshaded inner shape

Let us understand this through examples:

How to find the area of a shaded region in a triangle?

Let’s see a few examples below to understand how to find the area of a shaded region in a triangle.

Example 1

Calculate the area of the shaded region in the right triangle below.

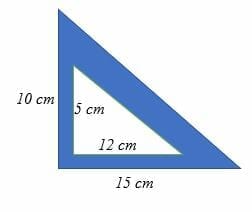
Solution

Area of shaded region = area of outer shape – area of the unshaded inner shape

Area of a triangle = ½ bh.

Area of outer shape = (½ x 15 x 10) cm².

= 75 cm².

Area of unshaded inner shape = (½ x 12 x 5) cm².

= 30 cm².

Area of shaded region = (75 – 30) cm².

= 45 cm².

Therefore, the area of the shaded region is 45 cm².

Example 2

Given AB = 6 m, BD = 8 m, and EC = 3 m, calculate the area of the shaded region in the diagram below.

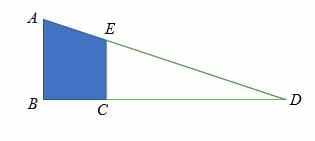
Solution

Considering similar triangles,

AB/EC = BD/CD

6/3 = 8/CD

Cross multiply.

6 CD = 3 x 8 = 24

Divide both sides by 6.

CD = 4 m.

Now calculate the area of triangle ABD and triangle ECD

Area of triangle ABD = (½ x 6 x 8) m²

= 24 m²

Area of triangle = (½ x 3 x 4) m²

= 6 m²

Area of the shaded region = (24 – 6) m²

= 18 m²

How to find the area of a shaded region in a rectangle?

Let’s see a few examples below to understand how to find the area of the shaded region in a rectangle.

Example 3

Calculate the area of the shaded region of the rectangle below if

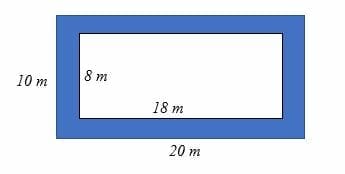
Solution

Area of shaded region = area of outer shape – area of unshaded inner shape

= (10 x 20) m² – (18 x 8) m²

= 200 m² – 144 m².

= 56 m²

Example 4

Given, AB = 120 cm, AF = CD = 40 cm and ED = 20 cm. Calculate the area of the shaded region of the diagram below.

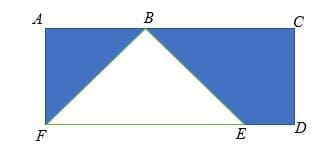
Solution

Area of the shaded region = area of the rectangle ACDF – area of triangle BFE.

Area of rectangle ACDF= (120 x 40) cm²

= 4,800 cm².

Area of triangle BFE = ½ x CD x FE

But FE = (120 – 20) cm

= 100 cm

Area = (½ x 40 x 20) cm².

= 400 cm².

Area of the shaded region = 4,800 cm² – 400 cm²

= 4,400 cm²

Example 5

Calculate the area of the shaded diagram below.

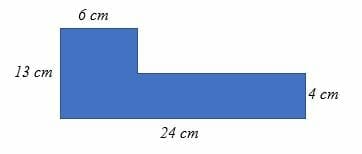
Solution

This is a composite shape; therefore, we subdivide the diagram into shapes with area formulas.

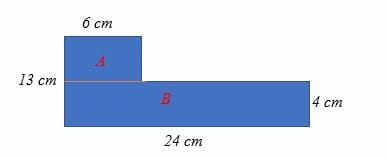
Area of the shaded region = area of part A + area of part B

= 6(13 – 4) cm² – (24 x 4) cm²

= 54 cm² + 96 cm²

= 150 cm².

So, the area of the shaded region is 150 cm²

How to find the area of a shaded region in a square?

Let’s see a few examples below to understand how to find the area of a shaded region in a square.

Example 6

Calculate the area of the shaded region in the diagram below.

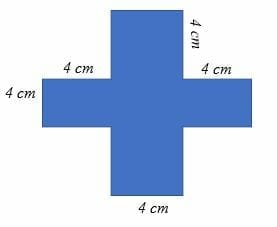
Solution

Area of the shaded region = area of the square – area of the four unshaded small squares.

The side length of the square = (4 + 4 + 4) cm

= 12 cm.

The side length of the four unshaded small squares is 4 cm each.

Area of the shaded region = (12 x 12) cm² –  4(4 x 4) cm²

= 144 cm² – 64 cm²

= 80 cm²

Example 7

Calculate the shaded area of the square below if the side length of the hexagon is 6 cm.

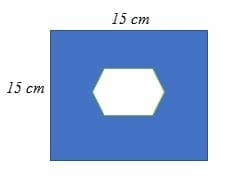
Solution

Area of the shaded region = area of the square – area of the hexagon

Area of the square = (15 x 15) cm²

= 225 cm²

Area of the hexagon

A = (L²n)/[4tan(180/n)]

A = (6² 6)/ [4tan (180/6)]

= (36 * 6)/ [4tan (180/6)]

= 216/ [4tan (180/6)]

= 216/ 2.3094

A = 93.53 cm²

Area of the shaded region = (225 – 93.53) cm².

= 131.47 cm²