Area of Squares – Explanation & Examples
As explained in the previous article about quadrilaterals, a square is a regular polygon with four equal sides and four right angles.
Now that you are already acquainted with the term area. In this article, you will learn about the area of a square and how to find the area using the area of a square formula.
How to Find the Area of a Square?
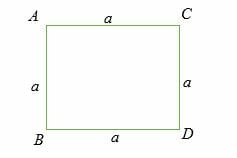
In the square ABCD shown below, the lengths AB = BD = DC = AC = a
The area of a square is, therefore, the region occupied inside the sides of a square. The measurement of the area is done in square units, with the standard unit being square meters (m2).
Area of a Square Formula
The area of a square can be calculated by drawing a square on a graph paper having 1 cm × 1 cm squares. After drawing the square, you can count the total number of complete squares and incomplete squares.
The area of the square is then approximated as;
Area = Number of complete squares + ½ (number of incomplete squares)
This method of finding an area of a square is just an approximation and cannot be used where accurate figures are required.
For this reason, let’s look at the most accurate formula for calculating the area of a square.
For a square of side length, a, the area of a square states that:
Area of a square = side × side
A = (a × a) sq. unit
Therefore,
Area of a square = a² square units
Alternatively, we can calculate the area of a square as:
Area of a square = a × a = (P/4) ² sq. units
where P = perimeter of a square.
Additionally, the area of a square can be calculated using its diagonal as;
Area of a square = 1/2 × (diagonal)² sq. units
But the diagonal of a square is calculated by Pythagorean theorem as,
Diagonal = √ (a² + a²) = √(2a2) = a√2
Where a = side length of a square.
Let’s work out a few example problems about the area of a square.
Example 1
Find the area of a square of side 20 m.
Solution
Area of a square = (a x a) Sq. unit
By substitution,
= (20 × 20) m2
= 400 m2
Example 2
Find the area of a square whose perimeter is 100 cm.
Solution
Perimeter of square = 100 cm
The perimeter of square = 4 × side
Therefore, 4 × side = 100 cm
Divide both sides by 4.
side = a = (100/4) cm = 25 cm
Now substitute a = 25 in the area of a square formula.
Area of a square = (25 x 25) cm2
A = 625 cm2
Therefore, the area of the square is 625 cm2
Example 3
Find the cost of cementing a square floor of side 13 m if the rate of cementing is $10 per m².
Solution
First, calculate the area of the square floor.
Area of a square = (a x a) Sq. unit
= (13 x 13) m2 = 169 m2
Now calculate the total cost of cementing by multiplying the area of the floor by the rate of cementing.
Cost = 169 m2 x $10 per m².
= $ 1690
Example 4
The length of a square football pitch is 150 m. Calculate the cost of grassing the pitch if the rate is $0.25/m2.
Solution
area = (150 x 150) = 22500 m2
The cost of grassing = 22500 m2 x $0.25/m2
= $5,625
Example 5
Find the area of a square lawn rounded by a path of 2 wide. Take the area of the path to be 160 m2.
Solution
Let the sides of the lawn be x, and the side of the lawn plus the path be x + 4.
Therefore,
The area of the path = (area of the lawn including the path) – (area of the lawn)
160 m2 = [(x * 4) (x + 4)] – (x * x)
160 = x² + 8x + 16 – x²
Simplify
160 = 8x + 16
Subtract 16 on both sides,
144 = 8x
Divide both sides by 8.
144/8 = x
18 = x
Therefore, the area of the lawn = (18 x 18) m2
= 324 m2
Example 6
A square courtyard’s floor, which 60 m, is to be covered by square tiles. Find the total number of tiles needed to completely cover the floor if the length of a tile is 2 m.
Solution
Calculate the area of both the square courtyard’s floor and the square tile.
Area of the courtyard’s floor = (60 x 60) m2 = 3600 m2
Area of a square tile = (2 x 2) m2 = 4 m2
To find the number of tiles needed to cover the courtyard’s floor, divide the area of the courtyard’s floor by the area of a tile.
Number of tiles = (3600 m2)/ 4 m2
= 900
Therefore, 900 tiles are needed to cover the courtyard’s floor completely.
