Area of Trapezoid – Explanation & Examples

To recall, a trapezoid, also referred to as a trapezium, is a quadrilateral with one pair of parallel sides and another pair of non-parallel sides. Like square and rectangle, a trapezoid is also flat. Therefore, it is 2D.

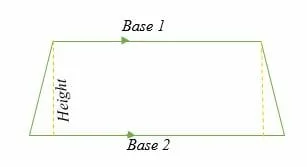
In a trapezoid, the parallel sides are known as the bases, while the pair of non-parallel sides are known as the legs. The perpendicular distance between the two parallel sides of a trapezium is known as a trapezoid height.

In simple words, the base and height of a trapezoid are perpendicular to each other.

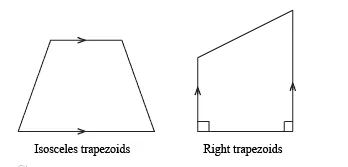
The trapezoids can be both right trapezoids (two 90-degree angles) and isosceles trapezoids (two sides of the same length). But having one right angle is not possible because it has a pair of parallel sides, which bounds it to make two right angles simultaneously.

In this article, you will learn:

• How to find the area of a trapezoid,
• How to derive the trapezoid area formula and,
• How to find the area of a trapezoid using the trapezoid area formula.

How to Find the Area of a Trapezoid?

The area of the trapezium is the region covered by a trapezium in a two-dimensional plane. It is the space enclosed in 2D geometry.

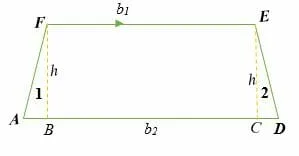
From the illustration above, a trapezoid is composed of two triangles and one rectangle. Therefore, we can calculate the area of a trapezoid by taking the sum of the areas of two triangles and one rectangle.

Derive the trapezoid area formula

Area of a trapezium ADEF = (½ x AB x FB) + (BC x FB) + (½ x CD x EC)

= (¹/₂ × AB × h) + (BC × h) + (¹/₂ × CD × h)

= ¹/₂ × h × (AB + 2BC + CD)

= ¹/₂ × h × (FE + AD)

But, FE = b₁ and AB = b₂

Hence, Area of a trapezium ADEF,

= ¹/₂ × h × (b₁ + b₂) ………………. (This is the trapezoid area formula)

Trapezoid Area Formula

According to the trapezoid area formula, the area of a trapezoid is equal to half the product of the height and the sum of the two bases.

Area = ½ x (Sum of parallel sides) x (perpendicular distance between the parallel sides).

Area = ½ h (b₁ + b₂)

Where h is the height and b_1, and b₂ are the parallel sides of the trapezoid.

How do you find the area of an irregular trapezoid?

An irregular trapezoid has nonparallel sides of unequal length. To find its area, you need to find the sum of the bases and multiply it by half of the height.

The height is sometimes missing in the question, which you can find using the Pythagorean Theorem.

How to find the perimeter of a trapezoid?

You know perimeter is a sum of all lengths of the outer edge of a shape. Therefore, the perimeter of a trapezoid is a sum of lengths of all 4 sides.

Example 1

Calculate a trapezoid area whose height is 5 cm, and the bases are 14 cm and 10 cm.

​Solution

Let b₁ = 14 cm and b₂ = 10 cm

Area of trapezoid = ½ h (b₁ + b₂) cm²

= ½ x 5 (14 + 10) cm²

= ½ x 5 x 24 cm²

= 60 cm²

Example 2

Find a trapezoid area with a height of 30 mm, and the bases are 60 mm and 40 mm.

Solution

Area of trapezoid = ½ h (b₁ + b₂) sq. units

= ½ x 30 x (60 + 40) mm²

= ½ x 30 x 100 mm²

= 1500 mm²

Example 3

The area of a trapezoid is 322 square inches. If the lengths of the two parallel sides of the trapezoid are 19 inches and 27 inches, find the trapezoid’s height.

Solution

Area of trapezoid = ½ h (b₁ + b₂) Sq. units.

⇒ 322 square inches = ½ x h x (19 + 27) Sq. inches

⇒ 322 square inches = ½ x h x 46 Sq. inches

⇒ 322 = 23h

Divide both sides by 23.

h = 14

So, the height of the trapezoid is 14 inches.

Example 4

Given that the height of a trapezoid is 16 m and one base’s length is 25 m. Calculate the dimension of the other base of the trapezoid if its area is 352 m².

Solution

Let b₁ = 25 m

Area of trapezoid = ½ h (b₁ + b₂) sq. units

⇒ 352 m² = ½ x 16 m x (25 m + b₂) sq. units

⇒ 352 = 8 x (25 + b₂)

⇒ 352 = 200 + 8b₂

Subtract 200 on both sides.

⇒ 152 = 8b₂

Divide both sides by 8 to get;

b₂ = 19

Therefore, the length of the other base of the trapezoid is 19 m.

Example 5

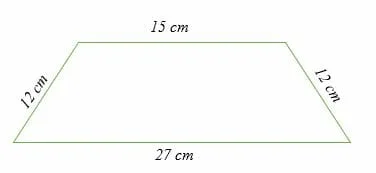
Calculate the area of the trapezoid shown below.

Solution

Since the legs (non-parallel sides) of the trapezoid are equal, then the height of the trapezoid can be calculated as follows;

To get the two triangles’ base, subtract 15 cm from 27 cm and divide by 2.

⇒ (27 – 15)/2 cm

⇒ 12/2 cm = 6 cm

12² = h² + 6²By Pythagorean theorem, the height (h) is calculated as;

144 = h² + 36.

Subtract 36 on both sides.

h² = 108.

h = 10.39 cm.

Hence, the height of the trapezoid is 10.39 cm.

Now, calculate the area of the trapezoid.

Area of trapezoid = ½ h (b₁ + b₂) Sq. units.

= ½ x 10.39 x (27 + 15) cm².

= ½ x 10.39 x 42 cm².

= 218.19 cm².

Example 6

One base of a trapezium is 10 m more than the height. If the other base is 18 m and the trapezoid area is 480 m², find the height and base of the trapezoid.

Solution

Let the height = x

Other base is 10 m than the height = x + 10.

Area of trapezoid = ½ h (b₁ + b₂) Sq. units.

By substitution,

480 = ½ * x * (x + 10 + 18)

480 = ½ *x * (x + 28)

Use the distributive property to remove the parentheses.

480 = ½x² + 14x

Multiply each term by 2.

960 = x² + 28x

x² + 28x – 960 = 0

Solve the quadratic equation to get;

x = – 48 or x = 20

Substitute the positive value of x in the equation of height and base.

Height: x = 20 m.

The other base = x + 10 = 10 + 20 = 30 m.

Therefore, the other base and height of the trapezoid are 30 and 20 m, respectively.