- Home
- >
- Arithmetic Series – Definition, Formula, and Examples
JUMP TO TOPIC
Arithmetic Series – Definition, Formula, and Examples
The arithmetic series is one of the first series you’ll encounter in math. Our understanding of the arithmetic series continuously expands throughout as well. The arithmetic series is one of the most fundamental series we’ll also learn in calculus, so understanding this topic by heart will also help us in understanding more complex series.
An arithmetic series contains the terms of an arithmetic sequence. Meaning, the difference between two consecutive terms from the series will always be constant.
We’ve established the foundation of arithmetic sequence before, so our discussion will now focus on how the arithmetic series’ definition and formula are established. We’ll also learn how to apply the arithmetic series’ formula to find different arithmetic series’ values and solve a variety of word problems.
What is an arithmetic series?
The arithmetic series represents the sum of the arithmetic sequence’s terms. The most important element of an arithmetic series (and arithmetic sequence, for that matter), is that the consecutive terms of the series will always share a common difference. We’ll explore the fundamental definition of arithmetic series and sequence then explore its summation forms as well. Let’s begin by observing the patterns below:
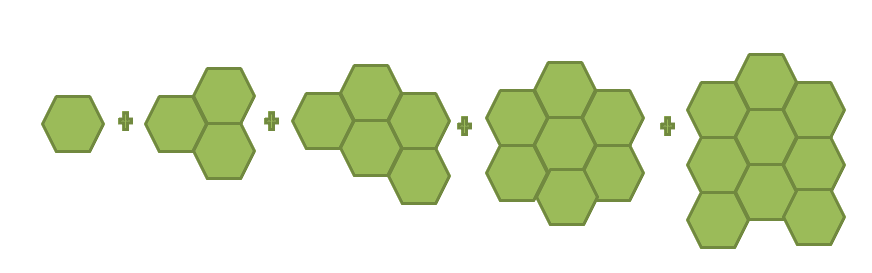
We see that for the next group of hexagons, the number of hexagons increases by $2$. To be exact, we have the following number of hexagons: $\{1, 3, 5, 7, 9\}$. Since each term increases by $2$ as we progress, we can conclude that $\{1, 3, 5, 7, 9\}$ is an arithmetic sequence. This becomes an arithmetic series when we express the sum of these terms and eventually find their sum. Here are a few more examples highlighting the difference between the arithmetic sequence and series.
| Arithmetic Sequence | Arithmetic Series | Common Difference |
| \begin{aligned}1, 3, 5, 7, 9, 11, …, 45\end{aligned} | \begin{aligned}1+ 3+ 5+ 7+ 9+ 11+…+ 45\end{aligned} | \begin{aligned}d =2\end{aligned} |
| \begin{aligned} 3, 6, 9, 12, 15, 18, …, 60\end{aligned} | \begin{aligned} 3 + 6 + 9 + 12+ 15+ 18+ …+60\end{aligned} | \begin{aligned}d =3\end{aligned} |
| \begin{aligned} -2, -4, -6, -8, -10, -12, …, -40\end{aligned} | \begin{aligned} -2 + (-4) + (-6) + (-8)+ (-10)+ (-12)+ …+(-40)\end{aligned} | \begin{aligned}d = -2\end{aligned} |
Now, let’s work with the general form of the arithmetic series and sequence: $a_1$ represents the first term of the series, $a_n$ represents the $n$th term, and $d$ represents its common difference. We have the following expressions for the arithmetic sequence and series:
| Arithmetic Sequence | \begin{aligned} a_1\underbrace{\phantom{x}} _{\color{Teal}+d}a_2\underbrace{\phantom{x}} _{\color{Teal}+d}a_3,…,a_{n-1}\underbrace{\phantom{x}} _{\color{Teal}+d}a_n\end{aligned} |
| Arithmetic Series | \begin{aligned} a_1\underbrace{+} _{\color{Teal}+d}a_2\underbrace{+} _{\color{Teal}+d}a_3+…+a_{n-1}\underbrace{+} _{\color{Teal}+d}a_n\end{aligned} |
We can also express the arithmetic series in summation notation as shown below:
\begin{aligned}S_n &= \sum_{i = 1}^{n} a_1\end{aligned}
Let’s now establish the formula to simplify $S_n$. Recall that $\boldsymbol{n}$th term can be expressed as $\boldsymbol{a_n = a_1 + (n-1)d}$. We can express all the terms of the series using this formula.
\begin{aligned}S_n &= a_1 + (a_1 + d) + (a_1 + 2d) + …+ [a_1 + (n -1)d]\end{aligned}
Why don’t we reverse the order of terms of $S_n$ and begin with $a_n$ instead? We’ll then end up subtracting $d$ from the previous term to find the next. Hence, we have the following:
\begin{aligned}S_n &= a_n + (a_n – d) + (a_n – 2d) + …+ [a_n + (n -1)d]\end{aligned}
Add the two equations to find the expression of the arithmetic series’ sum in terms of $a_1$, $a_n$, and $n$.
\begin{aligned}S_n &= a_1 + (a_1 + d) + (a_1 + 2d) + …+ [a_1 + (n -1)d]\\+\phantom{x}S_n&= \underline{a_n + (a_n – d) + (a_n – 2d) + …+ [a_n + (n -1)d]}\\2S_n &= \underbrace{(a_1 + a_n) + (a_1 + a_n) + …+ (a_1 + a_n)}_{n}\\2S_n &= n(a_1 + a_n)\\S_n&= \dfrac{1}{2}n(a_1 + a_n)\\&= \dfrac{n(a_1 + a_n)}{2}\end{aligned}
| $\boldsymbol{a_n}$ | \begin{aligned}a_n &= a_1 + (n -1)d\end{aligned} |
| $\boldsymbol{S_n}$ | \begin{aligned}S_n&= \dfrac{1}{2}n(a_1 + a_n)\\&= \dfrac{n(a_1 + a_n)}{2}\end{aligned} |
Here’s another way of proving the arithmetic series using its summation notation. Take a look at the section below and when you’re ready to learn how to apply what you’ve learned, head over to the next!
Arithmetic series formula’s proof using its summation notation
We can derive the formula for the sum of the arithmetic series by using the fact that the $n$th term of the arithmetic sequence is $a_n = a_1 + (n – 1)d$. This means that we can add $a_1, a_2, a_3,…, a_{n -1}, a_n$ and express its sum as shown below.
\begin{aligned}a_1+ a_2+ a_3+…+a_{n -1}+ a_n &=a_1 + (1 – 1)d + a_1 + (2 – 1)d +…+a_n + (n – 1)d\\&= \sum_{i = 1}^{n} [a_1 + (i – 1)d]\end{aligned}
We can separate the two summations as: $\sum_{i = 1}^{n} a_1$ and $\sum_{i = 1}^{n} (i – 1)d$. Let’s rewrite the two summations by expanding them then eventually simplify each group of terms.
| \begin{aligned}\boldsymbol{\sum_{i = 1}^{n} a_1}\end{aligned} | \begin{aligned}\boldsymbol{\sum_{i = 1}^{n} [a_1 + (i – 1)d]}\end{aligned} |
| \begin{aligned}\sum_{i = 1}^{n} a_1 &= \underbrace{a_1 + a_1 + … + a_1}_n\\&= a_1n\end{aligned} | \begin{aligned}\sum_{i = 1}^{n} (i – 1)d &= d\sum_{i = 1}^{n} (i – 1)\\&= d\left[\sum_{i = 1}^{n} i -\sum_{i = 1}^{n} 1 \right ]\\&= d\left[\dfrac{1}{2}n(n +1) – n \right ]\\&= \dfrac{1}{2}dn(n + 1) – dn\end{aligned} |
Adding these two groups of expressions, we have $\sum_{i = 1}^{n} a_1 = a_1n$ and $\ sum_{i = 1}^{n} [a_1 + (i – 1)d] = \dfrac{1}{2}dn(n + 1) – dn $.
\begin{aligned}\sum_{i = 1}^{n} [a_1 + (i – 1)d] &= \sum_{i = 1}^{n}a_1 + \sum_{i = 1}^{n} (i – 1)d\\&= a_1n + \dfrac{1}{2}dn(n + 1) – dn\\&= \dfrac{1}{2}n[2a_1 + d(n+ 1) – 2d]\\&= \dfrac{1}{2}n[2a_1 + d(n – 1)]\\&= \dfrac{1}{2}n[a_1 + {\color{Teal}a_1 + d(n – 1)}],\phantom{x}{\color{Teal}a_n=a_1 + d(n – 1)}\\&= \dfrac{1}{2}n(a_1 + a_n)\end{aligned}
This confirms that the arithmetic series’ formula is equal to $S_n = \dfrac{1}{2}n(a_1 + a_n)$. Now that we understand the arithmetic series’ definition and formula, let’s go ahead and focus on how we can apply this knowledge to solve problems.
How to solve arithmetic series?
When working with arithmetic sequences and series, always hold on to these two formulas:
| Finding the $\boldsymbol{n}$th term | \begin{aligned}a_n &= a_1 + (n -1)d\end{aligned} |
| Finding the sum of the arithmetic series | \begin{aligned}S_n&= \dfrac{1}{2}n(a_1 + a_n)\\&= \dfrac{n(a_1 + a_n)}{2}\end{aligned} |
Here are some helpful pointers when working on the arithmetic series:
- Take note of the values that are given. When the common difference, $d$, is not yet given, find the common value shared between the terms.
- If either $a_1$, $a_n$ or $n$ is missing, use the formula for $a_n$ to find the missing value.
- Once we have all three values, let’s now apply the sum formula for the arithmetic series.
Why don’t we apply what we’ve just learned by finding the sum of $3 + 8 + 13 + … +68 + 73$?
\begin{aligned}3\underbrace{ + }_{\color{Teal} + 5}8 \underbrace{+}_{\color{Teal} + 5}13 +…+68 \underbrace{+}_{\color{Teal} + 5} 73\end{aligned}
From this, we can confirm that we have an arithmetic series since each pair of consecutive terms share a common difference of $5$: $d = 5$. Use the formula for the $n$th term to find the value of $n$.
\begin{aligned}a_1 &= 3\\a_n&= 73\\d&= 5\\\\a_n &= a_1 + (n -1)d\\73 &= 3 + (n -1)5\\5(n -1)&= 70\\n -1 &= 14\\n &= 15\end{aligned}
This means that the arithmetic series, $3 + 8 + 13 + … +68 + 73$, contains $15$ terms. Evaluate the expression using the sum formula for arithmetic series, $S_n = \dfrac{1}{2}(n)(a_1 + a_n)$.
\begin{aligned} S_{15} &= \dfrac{1}{2}(15)(3 + 73)\\&= \dfrac{1}{2}(15)(76)\\&= 570\end{aligned}
This means that $3 + 8 + 13 + … +68 + 73 = 570$ and we’ve demonstrated how to use the two important formulas for the arithmetic series.
Example 1
In the arithmetic series, $-4 + -2 + 0 + 2 + 4 + …$, find the sum of the first $40$ terms.
Solution
Let’s first observe the series and determine the common difference shared between each pair of consecutive terms.
\begin{aligned}-4\underbrace{ + }_{\color{Teal} + 2}-2 \underbrace{+}_{\color{Teal} + 2}0 \underbrace{+}_{\color{Teal} + 2}2 \underbrace{+}_{\color{Teal} + 2} 4 + …\end{aligned}
From this, we can see that $d = 2$, so we can use this and $a_1 = -4$ to find the $40$th term of the series.
\begin{aligned}a_n &= a_1 + (n -1)d\\a_{40} &= -4 + (40 -1)2\\ a_{40} &= 74\end{aligned}
Now that we know the three important values, $\{a_1 = -4, a_n = 74, n =40\}$, we can now apply the sum formula for the arithmetic series.
\begin{aligned}S_n &= \dfrac{1}{2}(n)(a_1 + a_n)\\ S_{40}&= \dfrac{1}{2}(40)(-4 + 74)\\&= 1400\end{aligned}
This means that the sum of the first $40$ terms of the arithmetic series is $1400$.
Example 2
Evaluate the following expressions.
a. $\sum_{i = 1}^{50} (2i + 1)$
b. $\sum_{i = 3}^{20} (3i – 4)$
Solution
We’re now given arithmetic series in summation notation, so let’s review what the summation notation represents for the first item: $\sum_{i = 1}^{50} (2i + 1)$.
\begin{aligned}\sum_{\underbrace{i = 1}_{\text{initial value}}}^{\overbrace{50}^{\text{last value}}} \underbrace{(2i + 1)}_{\text{Equation representing the ith term}}\end{aligned}
This means that we’re working with $50$ terms and we can find the first ($a_1$) and fiftieth ($a_{50}$) terms by evaluating $2i + 1$ at $i = 1$ and $i = 50$.
| \begin{aligned}\boldsymbol{a_1}\end{aligned} | \begin{aligned}\boldsymbol{a_{50}}\end{aligned} |
| \begin{aligned}a_1 &= 2(1) + 1\\&= 3\end{aligned} | \begin{aligned}a_{50} &= 2(50) + 1\\&= 101\end{aligned} |
We can now use the sum formula for the arithmetic series,$S_n = \dfrac{1}{2}(n)(a_1 + a_n)$, to evaluate $\sum_{i = 1}^{50} (2i + 1)$.
\begin{aligned}\sum_{i = 1}^{50} (2i + 1) &= \dfrac{1}{2}(50)(3 + 101)\\&= 2600\end{aligned}
a. This means that $\sum_{i = 1}^{50} (2i + 1) = 2600$.
We’ll apply a similar process when evaluating $\sum_{i = 3}^{20} (3i – 4)$, but keep in mind that this time, we begin with $i =3$ and end with $i =20$, so this means that we’re working with $18$ terms. Let’s now work on finding the first and last terms of the arithmetic series by finding the values of $(3i -4)$ at $i =3$ and $i = 20$.
| \begin{aligned}\boldsymbol{a_1}\end{aligned} | \begin{aligned}\boldsymbol{a_{18}}\end{aligned} |
| \begin{aligned}a_1 &= 3(3) -4\\&= 5\end{aligned} | \begin{aligned}a_{18} &= 3(20) – 4\\&= 56\end{aligned} |
Apply the sum formula once more, but this time, use $n =18$, $a_1 = 5$, and $a_{18} = 50$.
\begin{aligned}\sum_{i = 3}^{20} (3i – 4)&= \dfrac{1}{2}(18)(5 + 56)\\&= 549\end{aligned}
b. Hence, we have $\sum_{i = 3}^{20} (3i – 4) = 549$.
Practice Questions
1. In the arithmetic series, $-3 + -6 + 0 + 3+ 6 + …$, find the sum of the first $30$ terms.
2. In the arithmetic series, $1+ 5 + 9 + 13 + 17 + …$, find the sum of the first $50$ terms.
3. Evaluate the following expressions.
a. $\sum_{i = 1}^{20} (i + 4)$
b. $\sum_{i = 1}^{40} (5i – 6)$
4. Evaluate the following expressions.
a. $\sum_{i = 4}^{60} (8i – 9)$
b. $\sum_{i = 5}^{40} (7i + 1)$
5. Alex observe that its clock strikes once when its hour hand is at $1$, twice at $2$, and the pattern continues. If she counts down the number of strikes, how many will she be able to count in $12$ hours?
Answer Key
1. $S_{30} =1215$
2. $S_{50} = 4950$
3.
a. $\sum_{i = 1}^{20} (i + 4) = 290$
b. $\sum_{i = 1}^{40} (5i – 6) = 3860$
4.
a. $\sum_{i = 4}^{60} (8i – 9) = 14079$
b. $\sum_{i = 5}^{40} (7i + 1) = 5706$
5. $78$ times
