Asymptote – Three Different Types, Properties, and Examples

Knowing how to determine and graph a function’s asymptote is important in sketching the function’s curve.  In this article, we will refresh your current knowledge of asymptotes. Our discussion will also show you how to use limits to find the asymptotes of a given function.

An asymptote is a straight line that a function approaches. Although asymptotes are not technically part of the function’s curve, they guide us in graphing the function accurately.

Since we will be discussing asymptotes and finding them through limits, make sure to have your notes on the following:

• Understanding what vertical, horizontal, and oblique asymptotes represent and how we can find them algebraically.
• Knowing how to evaluate limits through different limit laws and properties.
• Reviewing how asymptotes help us in sketching the curve of a function.

What is an asymptote?

Asymptotes represent the range of values that a function approaches as $x$ approaches a certain value. These asymptotes are graphed as a dashed vertical, horizontal, or slanted line.

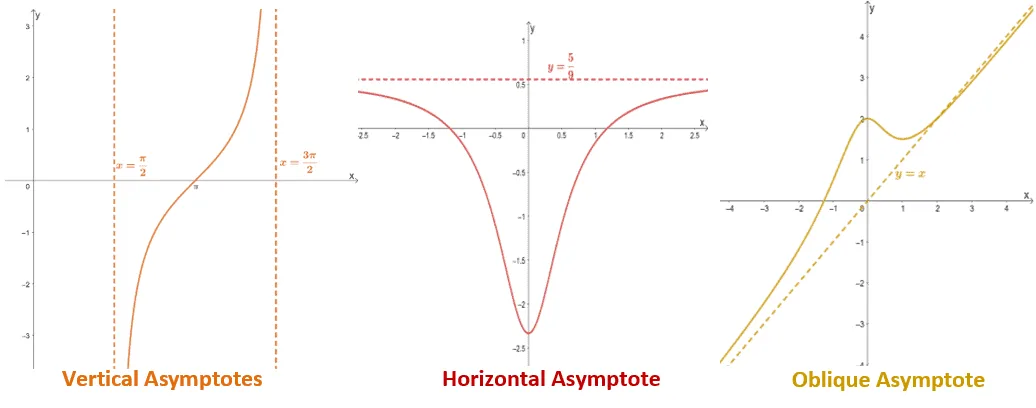
These three examples show how the function approaches each of the straight lines. Keep in mind though that there are instances where the horizontal and oblique asymptotes pass through the function’s curve. For vertical asymptotes, the function’s curve will never pass through these vertical lines.

There is a wide range of graph that contain asymptotes and that includes rational functions, hyperbolic functions, tangent curves, and more. Asymptotes are important guides when sketching the curves of functions. This is why it’s important that we know the properties, general forms, and graphs of each of these asymptotes.

Vertical asymptote

Vertical asymptotes are probably the first asymptote that you’ve encountered in your previous math classes. That’s because they represent the function’s restricted values for $\boldsymbol{x}$ throughout the function.

• For rational functions, these represent the values of $x$ that will return its simplified form’s denominator to $0$.
• For $\tan x$, these are the values of $x$ where $\cos x =0$.

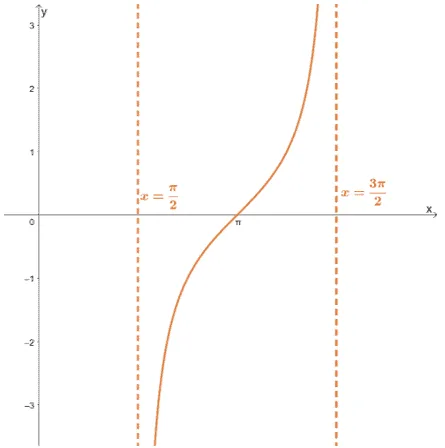
Vertical asymptotes are represented by vertical dashed lines. They have a general form of $\boldsymbol{x =a}$, and for each vertical asymptote, the line passes through $\boldsymbol{(a,0)}$.

We can extend this definition in terms of the function’s limits. If $x =a$ is an asymptote of $f(x)$, $f(x)$ satisfy either of the two or both conditions.

\begin{aligned}\lim_{x\rightarrow a^{-}} f(x) &= \pm \infty\\\lim_{x\rightarrow a^{+}} f(x) &= \pm \infty\end{aligned}

These are all the important properties of vertical asymptotes that we’ll need in order to find and graph them.

Horizontal asymptote

From its name, horizontal asymptotes are represented by horizontal dashed lines. These represent the values that the function approaches as $\boldsymbol{x}$ is significantly large or small.

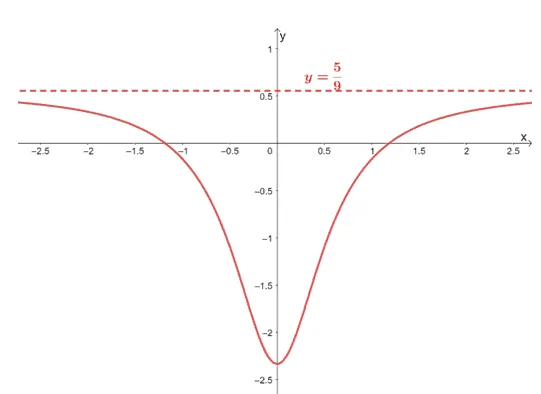
If the equation of $f(x)$’s horizontal asymptote is $y =b$, the limit of $\boldsymbol{f(x)}$ as $\boldsymbol{x}$ approaches infinity is as shown below.

\begin{aligned}\lim_{x\rightarrow \infty^{+}} f(x) &= b\\\lim_{x\rightarrow \infty^{-}} f(x) &= b\end{aligned}

When graphing $y =b$, make sure that the horizontal dashed line passes through $\boldsymbol{(0, b)}$. Horizontal asymptotes will also help us in graphing the function’s curve since we have an idea of where the function approaches as we stretch through both sides.

Oblique asymptote

The oblique asymptote is a slanted asymptote that is represented by a linear equation of the form, $\boldsymbol{y = mx +b}$. This occurs when the rational function’s numerator has a higher degree than the denominator.

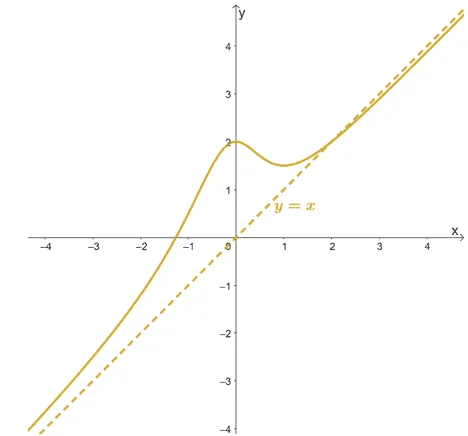
When we have $f(x) = g(x) + (mx +b)$, its oblique asymptote is $mx +b$ when the limit of $g(x)$ as $x$ approaches infinity is equal to 0. As with horizontal asymptotes, an oblique asymptote may pass through the function’s curve.

How to find asymptotes?

When given the graph of a function including its asymptotes, identifying the types of asymptotes will be straightforward.

• If you find a vertical dashed line, find the $x$-intercept that the asymptote passes through. Let’s say the asymptote’s $x$-intercept is $(a, 0)$, the function has a vertical asymptote at $x =a$.
• Similarly, when the asymptote is a horizontal line, find the $y$-intercept, $(0,b)$, that it passes through. The equation of the asymptote will be $y =b$.
• Now, when given an oblique asymptote, find two points passing through the slanted line. Use these two points to find the equation, $y =mx + b$, of the oblique asymptote.

Now, what if we only have the function’s expression? Use the three asymptotes’ definitions and conditions. We can evaluate the limits of the given function depending on the asymptote we’re looking for.

Finding the vertical asymptotes:

We can always begin by checking the function for a vertical asymptote. Check if the function has restricted values for $x$.

Let’s say we have $f(x) = \dfrac{x^2 – 16}{x^2 – 8x +16}$. Express $f(x)$ in factored form first then find the values of $x$ where the $f(x)$’s denominator is zero.

\begin{aligned}f(x) &= \dfrac{x^2 – 16}{x^2 – 8x +16}\\&= \dfrac{(x- 4)(x +4)}{(x +4)^2}\\&= \dfrac{x -4}{x +4}\end{aligned}

The denominator will be zero when $x = -4$, so $f(x)$ has a vertical asymptote at $x = -4$. When given a rational function, don’t forget to simplify it before finding its vertical asymptotes.

Finding the horizontal asymptotes:

When given a rational function, we can find the horizontal by observing the degrees of the numerator and denominator.

• If the denominator and numerator’s degrees are equal, we can divide the numerator’s leading coefficient by that of the denominator’s.
• When the denominator’s degree is greater than that of the numerator, the horizontal asymptote is equal to $y = 0$.

We can also determine a function’s horizontal asymptote by finding its limit as $\boldsymbol{x}$ approaches infinity. Use this approach to find the horizontal asymptote of $f(x) = \dfrac{x -1}{2x +3}$.

\begin{aligned} \lim_{x \rightarrow \infty}f(x)&= \lim_{x \rightarrow \infty} \dfrac{x -1}{2x + 3}\\&=\lim_{x \rightarrow \infty} \dfrac{x -1}{2x + 3} \cdot \dfrac{\dfrac{1}{x}}{\dfrac{1}{x}}\\&=\lim_{x \rightarrow \infty} \dfrac{1 -\dfrac{1}{x}}{2 + \dfrac{3}{x}}\\&= \dfrac{1 -0}{2 – 0}\\&= \dfrac{1}{2}\end{aligned}

This shows that the horizontal asymptote of $f(x)$ is $y = \dfrac{1}{2}$. We can double-check this by dividing the leading coefficients of $f(x)$’s numerator and denominator.

Finding the oblique asymptote:

When you’re working with a rational function, you can confirm that it has an oblique asymptote when the numerator’s degree is one degree greater than that of the denominator’s degree.

Rewrite $f(x)$ a sum of a linear expression and the remaining expression, $g(x)$.

\begin{aligned}f(x) &= (mx + b) + g(x)\\y_{\text{oblique}}&= mx +b + \lim_{x \rightarrow \infty} g(x) \\&= mx + b + 0\\&= mx + b\end{aligned}

When we have a rational function, we simply find the quotient of the numerator and the denominator and disregard the remainder.

Let’s say we have $f(x) = \dfrac{x^4-3x^3+2x^2-1}{x^3-4}$, we can find its oblique asymptote by rewriting $f(x)$ as $x – 3 + \dfrac{2x^2 + 4x -13}{x^3 – 4}$. We can confirm that $\lim_{x \rightarrow \infty} \dfrac{2x^2 + 4x -13}{x^3 – 4}$ is equal to zero as shown below.

\begin{aligned} \lim_{x\rightarrow \infty}\dfrac{2x^2 + 4x -13}{x^3 – 4} &= \lim_{x\rightarrow \infty}\dfrac{2x^2 + 4x -13}{x^3 – 4} \cdot \dfrac{\dfrac{1}{x^3}}{\dfrac{1}{x^3}}\\&=\lim_{x\rightarrow \infty}\dfrac{\dfrac{2}{x}+ \dfrac{4}{x^2} -\dfrac{13}{x^3}}{1 – \dfrac{4}{x^3}}\\&= \dfrac{0 + 0 – 0}{1 -0}\\&= 0\end{aligned}

A faster way is to find the quotient of $ x^4-3x^3+2x^2-1$ and$x^3 -4$. Hence, the oblique asymptote of $f(x)$ is $y= x -3$.

Keep in that when graphing horizontal and oblique asymptotes, account for the intersection between the asymptote and the function. Equate the function to the asymptote’s equation to find the intersecting point.

We’ve covered pretty much what we need to know about vertical, horizontal, and oblique asymptotes. Of course, the best way to master this topic is by finding and graphing the asymptotes of different functions.

Example 1

The graph of $f(x) = \dfrac{2x – 1}{x^2 – 9}$ is as shown below.

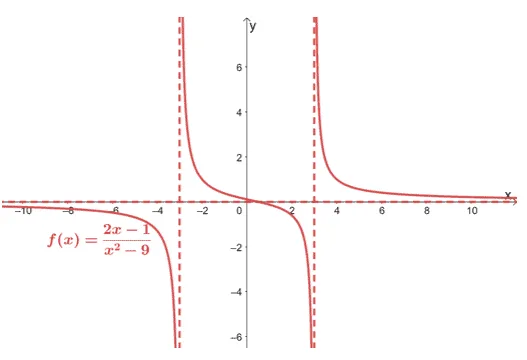
Use this graph to find the limits of the following:
a. $\lim_{x \rightarrow 3^{+}} f(x)$
b. $\lim_{x \rightarrow -3^{+}} f(x)$
c. $\lim_{x \rightarrow 3^{-}} f(x)$
d. $\lim_{x \rightarrow -3^{+}} f(x)$
e. $\lim_{x \rightarrow \infty^{+}} f(x)$
f. $\lim_{x \rightarrow -\infty^{-}} f(x)$

Solution
From the graph, we can see two dashed vertical lines and one dashed horizontal line. These three lines represent the vertical and horizontal asymptotes of $f(x)$.

• Since the vertical asymptotes pass through $(-3, 0)$ and $(3, 0)$, $f(x)$ has vertical asymptotes at $x = – 3$ and $x = 3$.
• Similarly, since the horizontal passes through $(0, 0)$, $f(x)$ has a horizontal asymptote at $y =0$.

In our discussion, recall that when the function has a vertical asymptote at $x =a$, $\lim_{x\rightarrow a^{-}} f(x)$ and $\lim_{x\rightarrow a^{+}} f(x)$ are both equal to $\infty$. The graph shown above confirms this since the vertical asymptotes go on forever at $x = 3$ and $x = -3$.

Hence, we have the following values for items a – d:

The horizontal asymptote tells us how the function behaves as it approaches both $-\infty$ and $\infty$. When we have the horizontal asymptote’s equation, $y =b$, we have $\lim_{x\rightarrow \infty^{-}} f(x) = b$ and $\lim_{x\rightarrow \infty^{+}} f(x) = b$.

We can use this property to find the limits shown in e and f.

 We can confirm this from the graph: $f(x)$’s curve approach $0$ as $x$ extends on both sides of the $xy$-coordinate system.

Example 2

Find the asymptotes of the function, $g(x) = \dfrac{4x}{x^3 + 8}$. Take a screen shot of the graph shown below then complete $g(x)$’s graph by sketching its asymptotes.

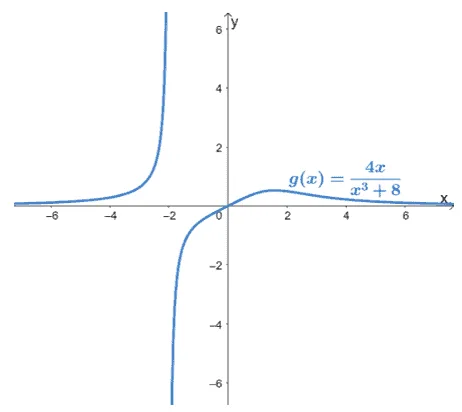
Solution
First, let’s check $g(x)$ for restricted values. Since $g(x)$ is rational function, let’s find the values of $x$ that will make the denominator equal to $0$.

\begin{aligned}x^3 + 8 &= 0\\ x^3 &= -8\\\sqrt[3]{x^3} &= \sqrt[3]{-8}\\x &= -2\end{aligned}

This means that $g(x)$ has a vertical asymptote at $x =- 2$. Since $g(x)$’s numerator has lesser degree than its denominator, $g(x)$ has a horizontal asymptote of $y =0$.

We can confirm this by evaluating $g(x)$’s limit as $x \rightarrow \infty$.

\begin{aligned}\lim_{x \rightarrow \infty} g(x) &=\lim_{x \rightarrow \infty} \dfrac{4x+8}{x^3 + 8}\\&= \lim_{x \rightarrow 2} \dfrac{\dfrac{d}{dx} (4x +8)}{\dfrac{d}{dx}(x^3 + 8)}\\&=\lim_{x \rightarrow \infty} \dfrac{4}{3x^2},\phantom{x}\color{Teal}\text{L’Hopital’s Rule}\\&=0 \end{aligned}

Since $\lim_{x \rightarrow \infty} g(x) = 0$, $y = 0$ is indeed $g(x)$’s horizontal asymptote. A function can’t have horizontal and oblique asymptotes at the same time, so we don’t need to check $g(x)$ for oblique asymptotes.

Let’s graph these two asymptotes on the given graph as shown below.

• Graph the vertical asymptote, $x= -2$, as a dashed vertical line that passes through $(-2, 0)$.
• Sketch a dashed horizontal line for $y0$. This asymptote passes through the origin, $(0, 0)$.

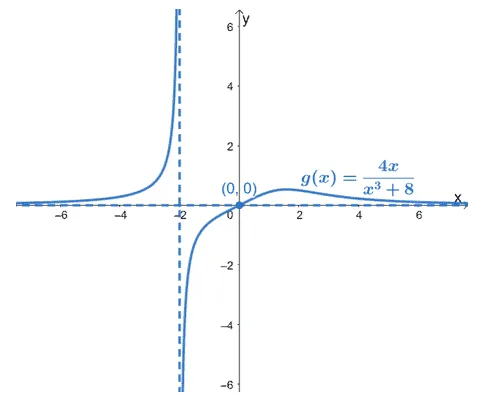
This graph shows $g(x)$’s curve plus its two asymptotes.

Example 3

Find the asymptotes of the function, $h(x) = \dfrac{2x^3 + 6x^2 – 9}{4 – x^2}$. Take a screen shot of the graph shown below then complete $h(x)$’s graph by sketching its asymptotes.

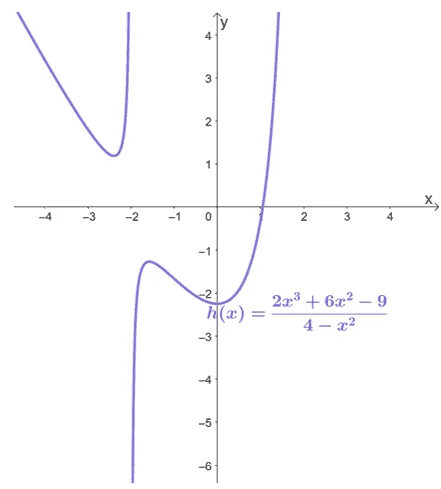
Solution
Let’s begin by finding the vertical asymptotes of $h(x)$ by equating $4 – x^2$ to zero. Values of $x$ that will make this equation true will make $h(x)$ undefined.

\begin{aligned}4- x^2 &= 0\\ x^2 &= 4\\\sqrt{x^2} &= \sqrt{4}\\ x&= \pm 2\end{aligned}

This means that $h(x)$ has two vertical asymptotes: $x= -2$ and $x = 2$.

Since $h(x)$’s numerator is one degree higher than its denominator, we’re expecting it to have an oblique asymptote. Write $h(x)$ in terms of its numerator and denominator’s quotient and remainder.

\begin{aligned}h(x) &= -2x – 6 + \dfrac{8x + 15}{4 -x^2}\end{aligned}

For oblique asymptotes, we only focus on the quotient, $-2x – 6$. This means that $h(x)$ has an oblique asymptote of $y= -2x – 6$.

As we have mentioned, we can’t have both a horizontal asymptote and an oblique asymptote, so there is no need for us to check $h(x)$ for any horizontal asymptotes.

Let’s go ahead and graph the two vertical asymptotes first: $x= -2$ and $x = 2$.Graph two dashed vertical lines. One passes through $(-2, 0)$ while the other passes through $(2, 0)$.

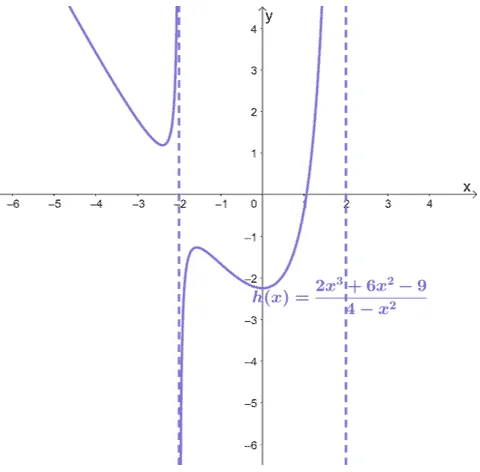
Before we graph the slanted asymptote, $y = -2x – 6$, let’s see if $h(x)$ and the oblique asymptote share a common point. Equate $-2x – 6$ to $\dfrac{2x^3 +6x^2 -9}{4- x^2}$ then find $x$.

\begin{aligned}-2x – 6 &= \dfrac{2x^3 +6x^2 -9}{4- x^2}\\(-2x – 6)(4 – x^2) &= 2x^3 + 6x^2 – 9\\2x^3 + 6x^2 – 8x -24 &= 2x^3 + 6x^2 – 9\\-8x – 24 &= -9\\-8x &= 15\\x&= -\dfrac{15}{8} \end{aligned}

This means that the oblique asymptote and $h(x)$ intersect at $\left(-\dfrac{15}{8}, h\left(-\dfrac{15}{8}\right)\right) = \left(-\dfrac{15}{8}, – \dfrac{9}{4}\right)$.This is the point we expect the curve and the oblique asymptote to intersect.

Now, to graph the oblique asymptote, let’s use $y= -2x-6$’s intercepts to graph its slanted line.

Let’s go ahead and graph the dashed slanted line now to complete the rational function’s graph.

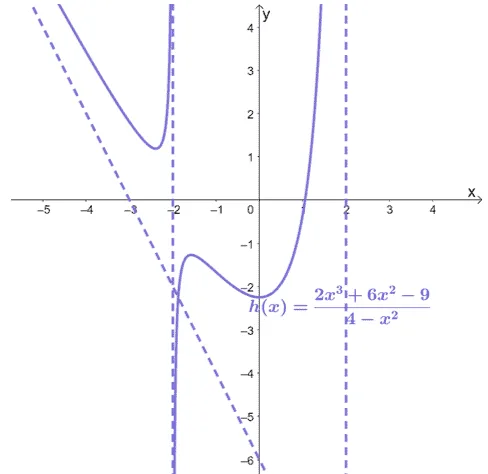
Example 4

Determine the values of $A$ and $B$ so that the graph of the function

\begin{aligned}f(x) &= \dfrac{Ax – 4}{3 – Bx}\end{aligned}

will have a vertical asymptote of $x = \dfrac{1}{2}$ and a horizontal asymptote of $y = -\dfrac{3}{2}$.

Solution

Since $f(x)$ has a vertical asymptote at $x= \dfrac{1}{2}$, $3 – Bx$ must be equal to $0$ when $x = \dfrac{1}{2}$.

\begin{aligned} 3 – B\cdot \dfrac{1}{2} &=0\\6 – B &= 0\\B &= 6\end{aligned}

Hence, for $x = \dfrac{1}{2}$ to be a vertical asymptote, $B$ must be equal to $6$. For $y = -\dfrac{3}{2}$ to be a horizontal asymptote, $\lim_{x \rightarrow \infty} f(x) = -\dfrac{3}{2}$.

\begin{aligned}\lim_{x \rightarrow \infty} f(x) &= \lim_{x \rightarrow \infty} \dfrac{Ax – 4}{3 – 6x} \\&= \lim_{x \rightarrow \infty} \dfrac{Ax – 4}{3 – 6x} \cdot \dfrac{\dfrac{1}{x}}{\dfrac{1}{x}}\\&= \dfrac{A – \dfrac{4}{x}}{\dfrac{3}{x}-6}\\&=\dfrac{A -0}{0 -6}\\&=- \dfrac{A}{6}\end{aligned}

Let’s equate $-\dfrac{A}{6}$ with $-\dfrac{3}{2}$ to find the value of $A$.

\begin{aligned}- \dfrac{A}{6}&=-\dfrac{3}{2}\\A &= 9\end{aligned}

Now that we have $A = 9$ and $B = 6$, $f(x) = \dfrac{9x – 4}{3 – 6x}$.

Practice Questions

1. The graph of $f(x) = \dfrac{4x – 1}{x^2 – 16}$ is as shown below.

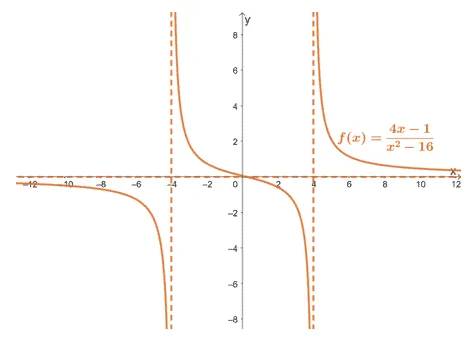
Use this graph to find the limits of the following:
a. $\lim_{x \rightarrow 4^{-}} f(x)$
b. $\lim_{x \rightarrow -4^{+}} f(x)$
c. $\lim_{x \rightarrow 4^{-}} f(x)$
d. $\lim_{x \rightarrow -4^{+}} f(x)$
e. $\lim_{x \rightarrow \infty^{+}} f(x)$
f. $\lim_{x \rightarrow -\infty^{-}} f(x)$
2. Find the asymptotes of the function, $g(x) = \dfrac{4x}{x^3 + 8}$. Take a screen shot of the graph shown below then complete $g(x)$’s graph by sketching its asymptotes.

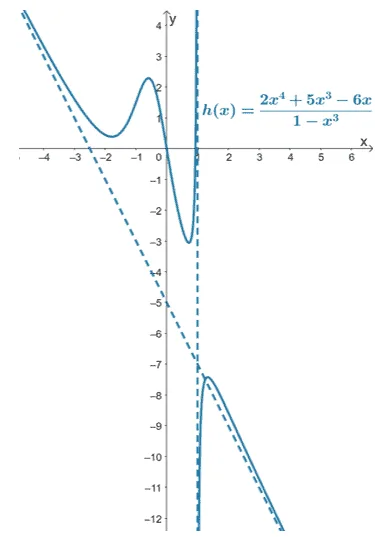
3. Find the asymptotes of the function, $h(x) = \dfrac{2x^4 + 5x^3 – 6x}{1 – x^3}$. Take a screen shot of the graph shown below then complete $h(x)$’s graph by sketching its asymptotes.

4. Determine the values of $A$ and $B$ so that the graph of the function
\begin{aligned}f(x) &= \dfrac{Ax + 1}{2 – Bx}\end{aligned}
will have a vertical asymptote of $x = \dfrac{1}{2}$ and a horizontal asymptote of $y = -\dfrac{3}{2}$.

Answer Key

1.
a. $\infty$
b. $\infty$
c. $\infty$
d. $\infty$
e. $0$
f. $0$
2.
Horizontal asymptote: $y = 0$
Vertical asymptote: $x =4$

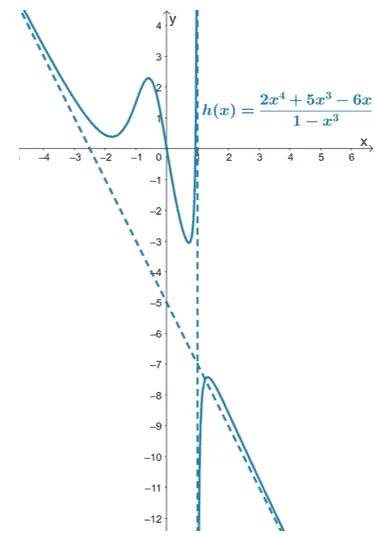
3.
Vertical asymptote: $x = 1$
Oblique asymptote: $y = -2x – 5$

4. $A =6 $ and $B = 4$

Images/mathematical drawings are created with GeoGebra.