- Home
- >
- Center of Mass – Definition, Formula, and Examples
JUMP TO TOPIC
Center of Mass – Definition, Formula, and Examples
 Integral calculus has a wide range of applications in physics and engineering and that includes finding the center of mass through integration. In this article, we’ll learn how to compute the center of mass of a given object through single and double integration.
Integral calculus has a wide range of applications in physics and engineering and that includes finding the center of mass through integration. In this article, we’ll learn how to compute the center of mass of a given object through single and double integration.
The center of mass represents the point within the object where the object is balanced horizontally when suspended from that given point. We can find the center of mass using definite integrals.
For us to learn to compute for the center of mass, it is essential that we know how to calculate for the area of the region enclosed by two curves. In case you need a quick refresher, head over to this link and check the article we wrote about this topic. We’ll also touch on the concept of moments briefly to better understand how we came up with the formula for the center of mass.
For now, let’s head over to the next section and understand the key components of the center of mass!
What is the center of mass?
The center of mass of an object is simply the point where the mass of the given object is equally distributed. When working with an object that has a uniform density, normally represented by $\rho$, the object’s center of mass will also be its geometric center called the centroid.
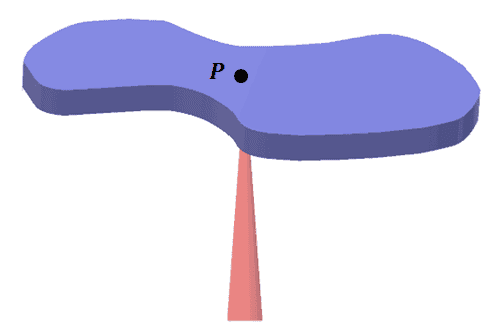
Throughout our discussion, we’ll learn how to find the value of the center of mass, labeled $P$ on the image shown. The point, $P$, is the object’s center of mass when it balances the region horizontally.
Before we dive right into the mathematical definition for the center of mass, let’s first understand what moments are and understand their significance when it comes to the object’s center of mass. Imagine that there’s a rod with a negligible mass and attached to it are two masses, $m_1$ and $m_2$.
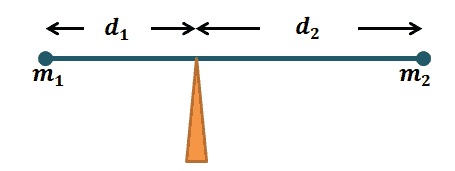
A fulcrum is situated somewhere in the middle of the rod with $m_1$ being $d_1$ units away from it while $m_2$ is $d_2$ units away. The rod will only stabilize when it satisfied the equation below:
\begin{aligned}m_1d_1 &= m_2d_2\end{aligned}
We can use this equation to find the position of the fulcrum. Now, extend this thought experiment and consider that the rod lies on the $x$-axis this time. With $m_1$ and $m_2$ positioned at $x_1$ and $x_2$, respectively. Let the center of mass be positioned at $\boldsymbol{\overline{x}}$. Extending the equation above, we now have:
\begin{aligned}m_1(\overline{x} – x_1) &= m_2(x_2 – \overline{x})\\\overline{x} &= \dfrac{m_1x_1 + m_2x_2}{m_1 + m_2}\end{aligned}
We call $m_1x_1$ and $m_2x_2$ as the moments of the two masses, $m_1$ and $m_2$, respectively. We can then extend this concept to a system of $m_1, m_2, m_3,…,m_n$ masses positioned at $x_1, x_2,x_3, …,x_n$. The center of mass of the system can be expressed as shown below.
\begin{aligned}\overline{x} &= \dfrac{\sum_{i =1}^{n} m_ix_i}{m}\end{aligned}
Keep in mind that the denominator, $m$, represents the total mass or $\sum_{i=1}^{n}m_i$. We call the sum of the moments the total moment about the origin.
When working with a coordinate system, we can express the center of mass as an ordered pair,$(\overline{x} \overline{y})$.
| \begin{aligned}\overline{x} &= \dfrac{M_y}{m}\end{aligned} | \begin{aligned}\overline{y} &= \dfrac{M_x}{m}\end{aligned} |
The variables, $M_x$ and $M_y$, represent the total moment about the $x$ and $y$-axis, respectively. We use these concepts to build up our understanding of the center of mass in terms of the functions’ curves and area.
Center of mass definition in terms of definite integral
We’ve covered the center of mass of discrete points, so let’s take a look at the center of mass of systems that are distributed continuously throughout a thin sheet of material. We’ll begin by observing that the sheet is thin enough that we can consider it as a two-dimensional figure we call the lamina.
When we assume that the lamina’s density is uniform, the lamina’s center of mass is solely dependent on its shape. This means that we’ll disregard its density first. We’ll apply a similar process to find the total mass and center of mass of the lamina.
By symmetry principle, recall that when the region is symmetric about a line, the centroid is set to be to lie on the region as well. For laminas that are rectangular in shape, we can guarantee that the center of mass (or centroid) is located at the center of the rectangle or where the diagonals intersect.
Now, let’s say we have a general lamina, $R$, where the region is bounded by two vertical lines, $x =a$ and $x =b$, as shown below.
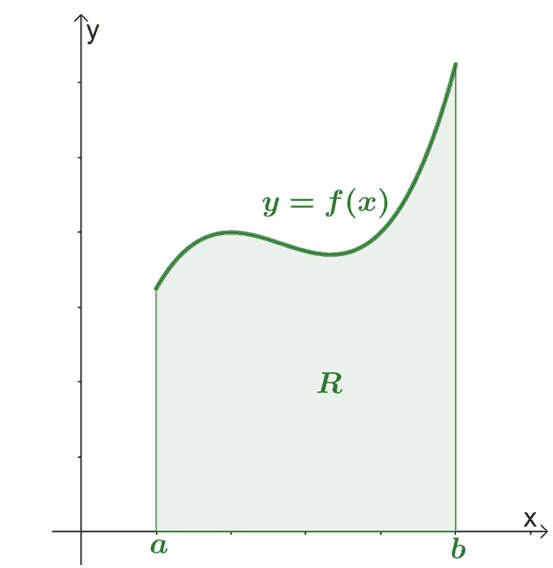
As with our earlier examples, we’ll have to find the total mass and moments of the lamina with respect to the vertical and horizontal axes. In the past, we’ve learned that we can estimate values like this by breaking down the area into smaller rectangles with uniform width throughout the interval, $[a, b]$.
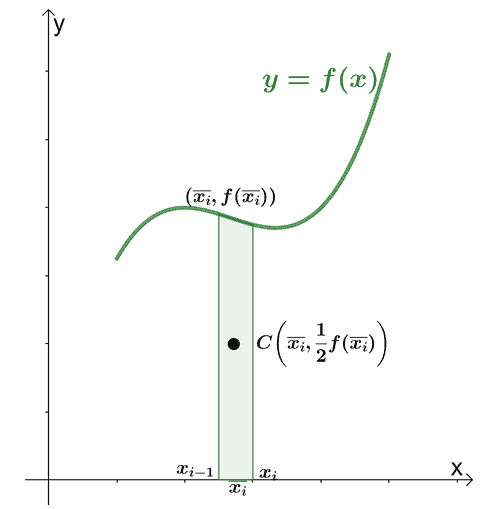
After dividing the rectangles into $n$ subintervals with the following endpoints, $\{x_0, x_1, x_2, x_3,..,x_n\}$, and each subinterval has a width of $\Delta x$. Let $\overline{x_i}$ be the $x$-coordinate of the rectangle’s centroid. Hence, we have $\overline{x_i} = \dfrac{x_{i -1} + x_i}{2}$, for each subinterval. We also have $\boldsymbol{\left(\overline{x_i}, \dfrac{1}{2}f(\overline{x_i})\right)}$ as the center of mass of the rectangle and $\boldsymbol{f(\overline{x_i}) \Delta x}$ as the area of the region. This means that the lamina has a mass of $\boldsymbol{\rho f(\overline{x_i}) \Delta x}$.
Center of mass formula using definite integrals
Finding the area between two curves is an extension of finding the area under the function’s curve. We can now derive the formula for the center of mass of the lamina using definite integrals.
Using these expressions, we can now estimate the mass systems with respect to the $x$ and $y$-axis.
- Find $M_y$ by adding all the moments $(m_i \overline{x_i})$.
- We apply a similar process for $M_x$ but use $\dfrac{1}{2}f(\overline{x_i})$ as the distance.
| \begin{aligned}\boldsymbol{M_y}\end{aligned} | \begin{aligned}\boldsymbol{M_x}\end{aligned} |
| \begin{aligned} M_y &= \lim_{n \rightarrow \infty} \rho \overline{x_i} f(\overline{x_i}) \Delta x\\&= \rho \int_{a}^{b} xf(x) \phantom{x}dx \end{aligned} | \begin{aligned} M_x &= \lim_{n \rightarrow \infty} \rho \overline{x_i}\frac{1}{2} [f(\overline{x_i})]^2 \Delta x\\&= \rho \int_{a}^{b} \frac{1}{2}[f(x)]^2 \phantom{x}dx \end{aligned} |
Using the fact that a plate’s mass is simply equal to the density times the area, we can calculate for the center of mass’ position.
\begin{aligned}m &= \rho \int_{a}^{b} f(x)\phantom{x}dx\end{aligned}
| Centroid’s $\boldsymbol{x}$-coordinate | Centroid’s $\boldsymbol{y}$-coordinate |
| \begin{aligned} \overline{x} &= \dfrac{M_y}{m}\\&= \dfrac{\rho \int_{a}^{b} xf(x) \phantom{x}dx}{\rho \int_{a}^{b}f(x) \phantom{x}dx}\\&= \dfrac{\int_{a}^{b}x f(x)\phantom{x}dx}{\int_{a}^{b} f(x)\phantom{x}dx}\end{aligned} | \begin{aligned} \overline{y} &= \dfrac{M_x}{m}\\&= \dfrac{\rho \int_{a}^{b} \frac{1}{2}[f(x) ]^2\phantom{x}dx}{\rho \int_{a}^{b}f(x) \phantom{x}dx}\\&= \dfrac{\int_{a}^{b}\frac{1}{2}[f(x) ]^2 f(x)\phantom{x}dx}{\int_{a}^{b} f(x)\phantom{x}dx}\end{aligned} |
This derivation also shows how a lamina’s center mass will not be affected by its density, $\rho$. We’ve learned that $\text{Area} = A = \int_{a}^{b} f(x)\phantom{x}dx$, so we can further rewrite the plate’s center of mass (and centroid) as shown below.
\begin{aligned} \boldsymbol{\overline{x}} &= \boldsymbol{\dfrac{1}{A}}\int_{\boldsymbol{a}}^{\boldsymbol{b}} \boldsymbol{x f(x)dx}\\ \boldsymbol{\overline{y}} &= \boldsymbol{\dfrac{1}{A}}\int_{\boldsymbol{a}}^{\boldsymbol{b}} \boldsymbol{\dfrac{1}{2}[f(x)]^2dx}\end{aligned}
We can use these two equations to determine the center of mass of the a given plate or lamina.
How to find the center of mass?
In the earlier sections, we’ve discussed how the center of mass is defined and how we came up with the formulas. Let’s now break down the steps we need to apply when finding the coordinates of the plate’s center of mass.
Step 1: Find the area of the region, $A = \int_{a}^{b} f(x) \phantom{x}dx$.
Step 2: Use the formula to find the center of mass’s $x$-coordinate, $\overline{x}$.
Step 3: Use the formula to find the center of mass’s $y$-coordinate, $\overline{y}$.
Step 4: Return the center of mass’ location as an ordered pair, $(\overline{x}, \overline{y})$.
Keep in mind that when the region is symmetric along the $y$-axis, there is no need for us to use the formula. Instead, we simply find the midpoint between the endpoints of $\boldsymbol{x}$. We’ve summarized the helpful formulas you’ll need when calculating for the $x$ and $y$-coordinates of the plate’s center of mass.
| Type of Region | $\boldsymbol{x}$-coordinate | $\boldsymbol{y}$-coordinate |
Area of region bounded by $f(x)$ and the $x$-axis: \begin{aligned}A&=\int_{a}^{b} f(x)\phantom{x}dx\end{aligned} | \begin{aligned}\overline{x} &= \dfrac{1}{A} \int_{a}^{b} xf(x)\phantom{x} dx\end{aligned} | \begin{aligned}\overline{y} &= \dfrac{1}{A} \int_{a}^{b} \dfrac{1}{2}[f(x)]^2\phantom{x} dx\end{aligned} |
Area of region bounded by two curves $(f(x) \geq g(x))$: \begin{aligned}A&=\int_{a}^{b} [f(x) – g(x)]\phantom{x}dx\end{aligned} | \begin{aligned}\overline{x} &= \dfrac{1}{A} \int_{a}^{b} x\left[ f(x)- g(x) \right]\phantom{x} dx\end{aligned} | \begin{aligned}\overline{y} &= \dfrac{1}{A} \int_{a}^{b} \dfrac{1}{2}\left\{[f(x)]^2 – [g(x)]^2\right\}\phantom{x} dx\end{aligned} |
We’ll show you different cases in our examples, so you can better understand how these steps are applied. Keep your notes handy and try to work along the problems as we explain each component!
Example 1
What is the center of mass of the plate that is bounded by the region shown below?
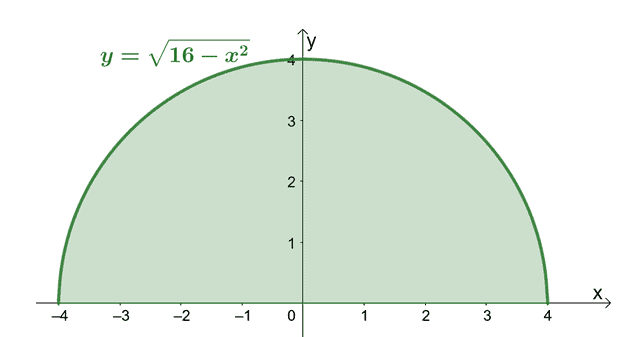
Solution
Although we can find the area under the curve of $y = \sqrt{16 – x^2}$ using definite integrals, it’s much easier and faster when we simply use our previous knowledge of semicircles. The area of a semicircle is equal to $\dfrac{1}{2}\pi r^2$, where $r$ is the semicircle’s radius.
\begin{aligned}A &= \dfrac{1}{2} \pi 4^2 \\&= 8\pi \end{aligned}
We can see that the semicircular plate is symmetric with respect to the $y$-axis, so there is no need for us to use the formula we’ve derived to find the $x$-coordinate of the center of mass. By the symmetry principle, we simply find the midpoint between $x= -4$ and $x = 4$, so $\overline{x} =0$.
Let’s now focus on calculating the $y$-coordinate of the center of mass using the formula, $\overline{y} = \dfrac{1}{A} \int_{a}^{b} \dfrac{1}{2}[f(x)]^2 \phantom{x}dx$.
\begin{aligned} A&= 8\pi\\ a&= -4\\ b&= 4 \end{aligned}
\begin{aligned} \overline{y} &= \dfrac{1}{8\pi} \int_{-4}^{4} \dfrac{1}{2}[\sqrt{16 – x^2}]^2 \phantom{x}dx\\ &= \dfrac{1}{8\pi} \int_{-4}^{4} \dfrac{1}{2}(16 – x^2 )\phantom{x}dx\\&= \dfrac{1}{8\pi} \cdot \dfrac{1}{2} \int_{-4}^{4} (16 – x^2 )\phantom{x}dx \\&= \dfrac{1}{16 \pi} \left[\int_{-4}^{4} 16\phantom{x}dx – \int_{-4}^{4} x^2\phantom{x}dx \right ]\\&= \dfrac{1}{16 \pi}\left\{\left[16x \right ]_{-4}^{4} – \left[\dfrac{x^3}{3} \right ]_{-4}^{4}\right\}\\&= \dfrac{1}{16 \pi}\left\{\left[16(4) -16(-4) \right ]_{-4}^{4} – \left[\dfrac{(4)^3}{3} -\dfrac{(-4)^3}{3} \right ]\right\}\\&= \dfrac{1}{16 \pi} \cdot \dfrac{128}{3}\\&= \dfrac{16}{3 \pi}\end{aligned}
We have $\overline{x} = 0$ and $\overline{y} = \dfrac{16}{3\pi}$, so the semicircular plate’s center of the mass is located at $\left(0, \dfrac{16}{3\pi}\right)$.
Example 2
Find the centroid of the region enclosed by the curve of $y = \sin x$ over the interval, $\left[0, \dfrac{\pi}{2}\right]$.
Solution
Here’s the sketch of the enclosed region and you use the graph as a guide. We’re looking for the actual coordinates of the center of mass (or centroid). This is marked as the black point on the $xy$-plane.
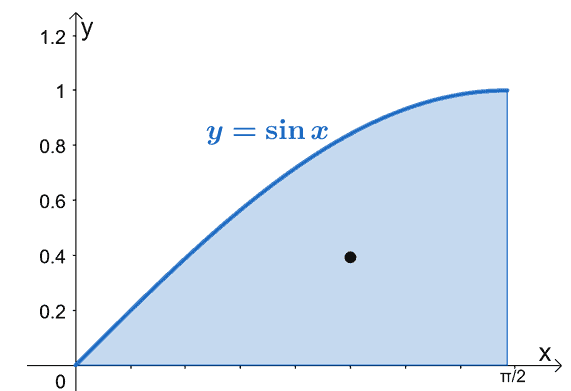
Begin by finding the area of the region enclosed by the curve and the interval, $\left[0, \dfrac{\pi}{2}\right]$.
\begin{aligned}A &= \int_{0}^{\frac{\pi}{2}} \sin x\phantom{x}{dx}\\&= [-\cos x]_{0}^{\pi/2}\\&= -\cos \dfrac{\pi}{2} – (-\cos 0)\\&= 0 -(-1)\\&= 1\end{aligned}
Let’s use $A =1$ and the formula, $\overline{x} = \dfrac{1}{A}\int_{a}^{b} xf(x) \phantom{x}dx$, to find the $x$-coordinate of the center of mass.
\begin{aligned}\overline{x} &= \int_{0}^{\pi/2} x\sin x \phantom{x}dx\end{aligned}
Use integration by parts to integrate the expression, $ \int x\cos x \phantom{x}dx$.
| \begin{aligned}u &= x\end{aligned} | \begin{aligned}dv &= \sin x \phantom{x}dx\end{aligned} |
| \begin{aligned}du &= dx\end{aligned} | \begin{aligned}v &= -\cos x\end{aligned} |
\begin{aligned} \int x\cos x \phantom{x}dx &= -x\cos x- \int -\cos x\phantom{x}{dx}\\&= -x\cos x + \sin x +C \end{aligned}
Use this expression to find the value of $\overline{x}$ as shown below.
\begin{aligned}\overline{x} &= [-x\cos x + \sin x]_{0}^{\pi/2}\\&= \left[\left(-\dfrac{\pi}{2}\cos\dfrac{\pi}{2} + \sin\dfrac{\pi}{2}\right) – (0 + \sin 0)\right]\\&= 1\end{aligned}
Now that we have the center of mass’ $x$-coordinate, let’s move on to finding its $y$-coordinate using the formula, $\overline{y}= \int_{a}^{b} \dfrac{1}{2}[f(x)]^2\phantom{x}dx$.
\begin{aligned}\overline{y} &= \int_{0}^{\pi/2} \dfrac{1}{2} \sin^2 x\phantom{x}dx\\&= \dfrac{1}{2}\int_{0}^{\pi/2}\sin^2 x\phantom{x}dx\end{aligned}
Use the fact that $\sin^2 x = \dfrac{1 – \cos 2x}{2}$ to integrate $\int \sin^2 x dx$.
\begin{aligned}\dfrac{1}{2}\int\sin^2 x\phantom{x}dx &= \dfrac{1}{2}\int\left(\dfrac{1 – \cos 2x}{2} \right )\phantom{x}dx\\&= \dfrac{1}{4}\int( 1- \cos 2x)\phantom{x}dx\\&= \dfrac{1}{4}\left(\int 1 \phantom{x}dx – \int \cos 2x \phantom{x}dx \right)\\&= \dfrac{1}{4}\left(x – \dfrac{1}{2}\sin 2x \right )+ C\end{aligned}
Use this expression to find the exact value of $\overline{y}$.
\begin{aligned}\overline{y} &= \dfrac{1}{2}\left[\dfrac{1}{4}\left(x – \dfrac{1}{2}\sin 2x \right ) \right ]_{0}^{\frac{\pi}{2}}\\&= \dfrac{1}{8}\left[\left(\dfrac{\pi}{2} – \dfrac{1}{2}\sin\pi \right ) -\left(0 – \dfrac{1}{2}\sin0 \right ) \right]\\&= \dfrac{\pi}{8}\end{aligned}
Since $\overline{x} =1$ and $\overline{y}= \dfrac{\pi}{8}$, the center of mass or centroid of the enclosed region is found at $\left(1, \dfrac{\pi}{8}\right)$.
Example 3
Find the center of mass of the region enclosed by the graphs of $y = 2x$ and $y = x^2$.
Solution
Graph the two curves to check which of the two is lying above the other. The graph can also show us the intersection between two points. We can also find the points of intersection algebraically by equating $2x$ and $x^2$.
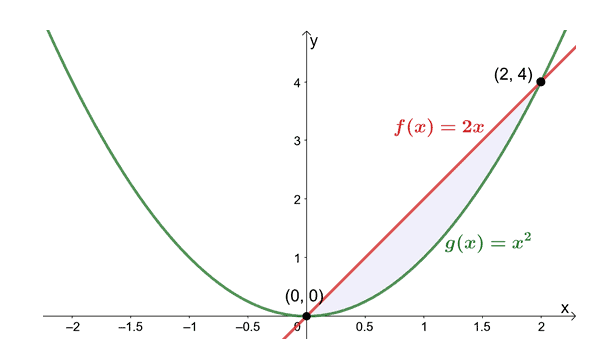
This means that we’re finding the centroid of the region enclosed by the two curves over the interval of $[0, 2]$. Let’s now find the area between these two curves by integrating $f(x) – g(x)$ over the $[0, 2]$.
\begin{aligned}A &= \int_{0}^{2} [f(x) – g(x)]\phantom{x}dx\\&= \int_{0}^{2} 2x – x^2 \phantom{x}dx\\&=\int_{0}^{2} 2x \phantom{x}dx-\int_{0}^{2} x^2\phantom{x}dx\\&= 2\int_{0}^{2} x \phantom{x}dx-\int_{0}^{2} x^2\phantom{x}dx\\&= 2\left[\dfrac{x^2}{2} \right ]_{0}^{2} – \left[\dfrac{x^3}{3}\right]_{0}^{2}\\&= 2\left(\dfrac{2^2}{2}-0 \right )- \left(\dfrac{2^3}{3}-0 \right )\\&= \dfrac{4}{3}\end{aligned}
Use the formulas for the coordinates of the centroid when the region is bounded by two curves.
| $\boldsymbol{x}$-coordinate | $\boldsymbol{y}$-coordinate |
| \begin{aligned}\overline{x} &= \dfrac{1}{A} \int_{a}^{b} x\left[ f(x)- g(x) \right]\phantom{x} dx\end{aligned} | \begin{aligned}\overline{y} &= \dfrac{1}{A} \int_{a}^{b} \dfrac{1}{2}\left\{[f(x)]^2 – [g(x)]^2\right\}\phantom{x} dx\end{aligned} |
Apply the fundamental integral properties and antiderivative formulas to evaluate the two definite integrals. We’ve summarized the calculations for you in this table. Use the final values to locate the centroid’s position, $(\overline{x}, \overline{y})$.
| \begin{aligned}\boldsymbol{\overline{x}}\end{aligned} | \begin{aligned}\boldsymbol{\overline{y}}\end{aligned} |
| \begin{aligned}\overline{x} &= \dfrac{1}{4/3} \int_{0}^{2} x(2x- x^2)\phantom{x} dx\\&= \dfrac{3}{4}\int_{0}^{2} (2x^2 -x^3)\phantom{x}dx\\&= \dfrac{3}{4}\left[2\int_{0}^{2} x^2\phantom{x}dx -\int_{0}^{2} x^3\phantom{x}dx\right]\\&= \dfrac{3}{4}\left\{2\left[\dfrac{x^3}{3} \right]_{0}^{2} -\left[\dfrac{x^4}{4} \right]_{0}^{2}\right\}\\&= \dfrac{3}{4}\left[2\left(\dfrac{2^3}{3} -0 \right )-\left(\dfrac{2^4}{4} -0 \right ) \right ]\\&= 1\end{aligned} | \begin{aligned}\overline{y} &= \dfrac{1}{4/3} \int_{0}^{2} \dfrac{1}{2}\left[ (2x)^2- (x^2)^2\right ]\phantom{x} dx\\&= \dfrac{3}{4}\cdot\dfrac{1}{2}\int_{0}^{2} (4x^2 -x^4)\phantom{x}dx\\&= \dfrac{3}{8}\left[4\int_{0}^{2} x^2\phantom{x}dx -\int_{0}^{2} x^4\phantom{x}dx\right]\\&= \dfrac{3}{8}\left\{4\left[\dfrac{x^3}{3} \right]_{0}^{2} -\left[\dfrac{x^5}{5} \right]_{0}^{2}\right\}\\&= \dfrac{3}{8}\left[4\left(\dfrac{2^3}{3} -0 \right )-\left(\dfrac{2^5}{5} -0 \right ) \right ]\\&= \dfrac{8}{5}\end{aligned} |
From this, we can see that the $x$-coordinate of the center of mass is $1$ while the $y$-coordinate is $\dfrac{8}{5}$. Hence, the centroid is located at $\left(1, \dfrac{8}{5}\right)$.
Practice Questions
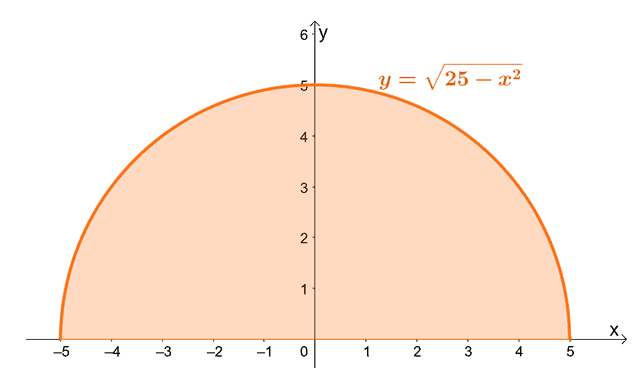
1. What is the center of mass of the plate that is bounded by the region shown below?
2. Extend your understanding and find a general expression for the center of mass of the semicircular plate that has a radius $r$.
3. Find the centroid of the region enclosed by the curve of $y = \cos x$ over the interval, $\left[0, \dfrac{\pi}{2}\right]$.
4. Find the center of mass of the region enclosed by the graphs of $y = 4x$ and $y = 3x^2$.
5. What is the center of mass of the plate that is bounded by the curves of $y = x^3$ and $y = x^2$.
Answer Key
1. $\left( 0, \dfrac{20}{3\pi}\right)$
2. $\left( 0, \dfrac{4r}{3\pi}\right)$
3. $\left(\dfrac{\pi}{2} – 1, \dfrac{\pi}{8}\right)$
4. $\left(-1, -\dfrac{16}{5}\right)$
5. $\left( \dfrac{3}{5}, \dfrac{12}{35}\right)$
Images/mathematical drawings are created with GeoGebra.
