Circles – Explanation & Examples

One of the important shapes in geometry is the circle. A geometry-based exam will have most of the questions consist of rectangles, triangles, and circles.

We’ve all seen circles before. They have this perfectly round shape, which makes them perfect for hula-hooping! This article will explain what a circle is, its properties, and its parts.

What is a Circle in Geometry?

The word ‘circle’ is derived from a Greek word that means ‘hoop’ or ‘ring.’ In geometry, a circle is defined as a closed two-dimensional figure in which the set of all the points in the plane is equidistant from a given point called “center.”

Never confuse a circle with a polygon. A circle is not a polygon because it is made up of curves.

The history of the circle is ancient. People used to believe that the moon, sun, and other planets are circular because there was no concept of 3D shapes—mathematicians study circles which helped them develop calculus and astronomy.

In 1700 BC, Rhind Papyrus proposed a method to find the area of a circle. At that time, the value of pi was not accurate. In 300 BC, Euclid stated the properties of circles in his book. Finally, in 1880 AD, a German mathematician, Lindemann, solved the issue with pi’s value and proved that pi is a transcendental (not a root of any polynomial with rational coefficients) number.

Circles are all around us! Some of the real-world examples of circles are:

• The wheel of a bicycle
• Coin
• Dinner plate
• Wall clock
• Ferris wheels

Therefore, a circle is an important shape in the field of geometry. Let’s look at the parties and properties of a circle.

Parts of a Circle

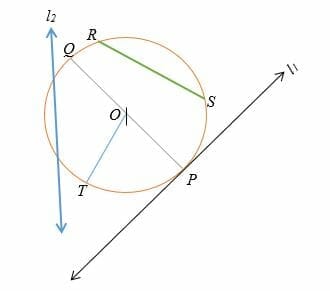
• Center: The center is the midpoint of a circle. In the above diagram, the center of the circle point ‘O’.
• Radius: This is a line segment from the center of a circle connecting any point on the circle itself. The radius of a circle is denoted by either letter “r” (lower case) or “R” (upper case).

Line OT is the radius of the above circle.

• Diameter: The diameter of a circle is a line segment passing through the center of a circle and having both the circle’s endpoints. Mathematically, the diameter is two times the radius of a circle. The diameter of a circle is denoted by “D” or “”

Line PQ is the diameter of the circle.

• Chord: A chord is a line segment with both the endpoints on the circle. Line RS is the chord of the circle above. The diameter of a circle is the longest chord.
• Secant: A secant is an extended chord of a circle.

Line 2 (l₂) is the secant of the circle above.

• Arc: An arc is a curve along the outer line of the circle
• Tangent: The tangent of a circle is a straight line that externally touches a circle, the circle’s outer line. Line 2 (l₂) is the tangent of the circle.
• Segment: A segment is a region bound by an arc and a chord.
• Sector: A sector is a region by an arc and two radii. Region OTP is the sector of the circle, as illustrated above.
• Circumference: The circumference of a circle is the total distance all-round the outer line of a circle
• Area of a circle: The region bounded by the outer line of a circle
• Annulus: An annulus is a ring-shaped object formed between two concentric (circles with a common center) circles. For instance, the shaded region in the circle below is called the annulus.

Properties of a Circle

There exist several facts about circles. These facts about circles are known as the properties of the circle. Let’s examine them.

• Circles with equal radii or diameters are congruent.
• The longest chord of a circle is called the diameter.
• The diameter of a circle is twice the radius of the circle itself.
• The diameter divides the circle into two equal halves.
• The outer line of a circle is equidistant from the center.
• Regardless of the measure of the radii or diameters, all circles are similar.
• The radius is a perpendicular bisector of the chord.
• Two or more chords are equal in lengths if they are all equidistant from the center of a circle.
• The angle formed between the radius and the tangent line is always 90 degrees (right angle)
• Two tangents are equal if they have a common point of origin.
• The angle subtended at the center of a circle by its circumference is equal to four right angles.
• The circumference of two or more different circles is proportional to their corresponding radii.
• Arcs of the same circle are proportional to their corresponding angles.
• The radii of equal circles or the same circle are equal.
• Equal circles have areas and equal circumferences.
• The distance between the longest chord and the center of a circle is zero.
• The perpendicular distance center of the circle to the chord increases as the chord’s length decreases, and vice versa.
• A circle can circumscribe polygons such as a triangle, trapezium, rectangle, etc.
• Similarly, a circle can be inscribed inside a polygon such as a rectangle, kite, square, trapezium, etc.
• Tangents drawn at both two ends of the diameter are always parallel to each other.
• Two radii joining the ends of a chord to the center of a circle form an isosceles triangle.
• Equal arcs subtend equal angles at the center of the circle.

Example 1

Which of the following things is circular in shape?

1. Pizza
2. Football
3. Orange
4. All of these.

Solution

All of the mentioned shapes are circular in shape.

Therefore, the correct choice is D.

Example 2

A circular bowl has a diameter of 9 inches. What is the radius of the bowl?

Solution

We know that the radius of the circle is half of the diameter.

Therefore,

Radius = 9/2 = 4.5 inches

Example 3

Which of the following parts of a circle can also be a chord of a circle?

1. Radius
2. Diameter
3. Arc
4. Sector

Solution

A chord is a line segment with both the endpoints on the circle. The diameter of a circle is the longest chord.

Hence, the correct choice is B.