• Home
  • >
  • Comparing Fractions – According to the Denominators

Comparing Fractions – According to the Denominators

Comparing FractionsHow to Compare Fractions?

Comparing fractions is actually the process telling if the one fraction is less than, greater than, or equal to another. Symbols for comparison similarly are used done with a comparison of whole numbers.

For instance, the following sentences can mathematically be represented as follows:
3 is less than 8 would be written as 3 < 8. 14 is greater than 2 would be written as 14 > 2.

17 is equal to 17 would be written as 17 = 17.

It, therefore, is possible to do the same thing with fractions. Let’s begin with fractions common denominators.

The standard method of comparing two fractions is by finding the equivalent fractions that have the same denominator. For example, to compare 1/2 and 1/3, multiply each fraction by the reciprocal of another’s denominator.

1/2 x 1/3= 3/6 and 1/3 x 1/2 = 2/6.

3/6 > 2/6. Therefore, 1/2 > 1/3

Comparing Fractions with Different Denominators

There are several methods of comparing fractions when the denominators are different. These are:

1. Get the common denominators.

For example, to compare 4/5 and 2/9, these are the steps using the common denominator method:

Steps:

  • Multiply numerator and denominator of each fraction by the denominator of another; 4/5 = 4/5 x 9/9 = 36/45 and 2/9 = 2/9 x 5/5 = 10/45.
  • Now that the denominator is common, the numerators are compared.
  • Since 36 > 10, therefore, 4/5 > 2/9 or 2/9 < 4/5.

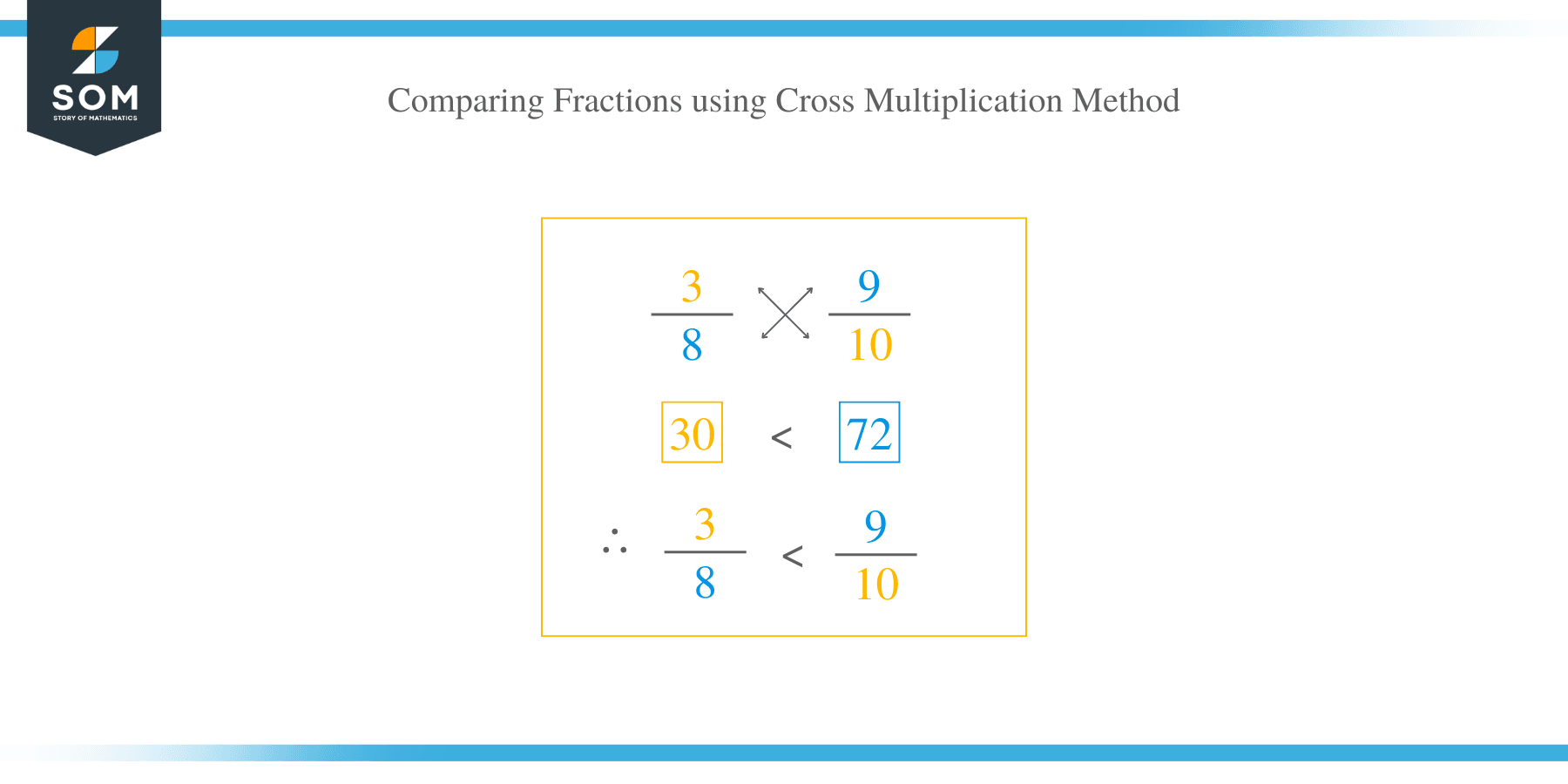
2. Use of cross multiplication method

Compare 3/8 and 9/30.

Steps:

  • Cross multiply 3/8 and 9/10 and make sure you write the product at the top of the fraction.
  • 3/8 cross multiply with 9/10 = 3 x 10 = 30 and 8 x 9 =72.
  • Now compare the products as: 30 < 72, and so, 3/8 < 9/10.Comparing Fractions using Cross Multiplication Method

3. Simplification method

Compare 20/35 and 8/14.

These fractions can be compared after simplification as show below:

  • 20/35 = (20 ÷ 5)/(35 ÷ 5) = 4/7 and 8/14 = (8 ÷ 2)/(14 ÷ 2) = 4/7.
  • Both fractions have been simplified to an equivalent value, and therefore, 20/35 = 8/14.

4. Convert the Fractions to Decimals

By dividing the numerator by each fraction’s denominator, fractions can be converted to decimals, and comparisons are made.

Compare 3/4 and 4/5.

In this case, equivalent decimal fractions are:

  • 3/4 = 0.75 and 4/5 = 0.8.
  • Since 0.75 < 0.80, then 3/4 < 4/5.

Examples:

  1. Which one is greater, 4/7 or 3/5?

Solution

Calculate the L.C.M. of the denominators 7 and 5 = 35

Divide both sides of the fractions by the L.C.M.

35 ÷ 7 = 5

35 ÷ 5 = 7

Multiply the denominator and numerator by the answer you get after division.

4 × 5/7 × 5 = 20/35

3 × 7/5 × 7 = 21/35

Since, 21/35 > 20/35

And so, 3/5 > 4/7

The above problem can be solved by cross multiplication method as show below:

4 × 5 = 20

3 × 7 = 21

And because, 21 > 20

Thus, 3/5 > 4/7

  1. Compare the following fraction: 32/5 and 2 ¾.

Solution

First the mixed fraction into improper fraction.

2 ¾ = (4 × 2) + ¾ = 11/4

3 2/5 = (5 × 3) + 2/5 = 17/5

Now by cross multiplication of 11/4 and 17/5

11 × 5 = 55

17 × 4 = 68

Since 68 > 55.

Thus, 17/5 > 11/4

Or, 32/5 > 2 ¾

  1. Compare the following fractions and put < or > sign between them accordingly:

a. 1/4 and 3/4

Solution

In this case,the denominator of each fraction 4. Therefore, the numerator 1 < 3 and thus,

1/4<3/4.

b. 2/3and 3/4

Solution

The LCM of denominator = 12

Therefore, 2/3 = 2/3 × 4/4 =8/12

And, 3/4 = 3/4×3/3 = 9/12

Since 8 < 9

Therefore, 2/3<3/4.

c. Compare: 3/5 and 5/3

Solution

Find the L.C.M. of 5 and 3 = 15

Therefore, 3/5 = 3/5 × 3= 9/15

5/3 = 25/15

Since, 9 < 25

Thus, 9/15 < 25/15.

Practice Questions

1. $3/8 =\blacksquare/24$

What must the value of $\blacksquare$ be to make the equation true?

2. $4/9 =16/\blacksquare$

What must the value of $\blacksquare$ be to make the equation true?

3. $8/12 =24/\blacksquare$

What must the value of $\blacksquare$ be to make the equation true?

4. $2/9 =\blacksquare/ 36$

What must the value of $\blacksquare$ be to make the equation true?

5. $5/6 =25/\blacksquare$

What must the value of $\blacksquare$ be to make the equation true?

6. $4/7 = \blacksquare/35$

What must the value of $\blacksquare$ be to make the equation true?

7. $9/9 = \blacksquare/27$

What must the value of $\blacksquare$ be to make the equation true?

8. $1/4 = \blacksquare/36$

What must the value of $\blacksquare$ be to make the equation true?

9. Is the inequality, $\dfrac{6}{12} < \dfrac{3}{2}$, true or false?

10. Is the inequality, $\dfrac{3}{15} < \dfrac{1}{4}$, true or false?

11. Is the inequality, $\dfrac{12}{36} > \dfrac{3}{4}$, true or false?

12. Is the inequality, $\dfrac{8}{4} > \dfrac{9}{3}$, true or false?

13. Which of the following will make the statement, $\dfrac{1}{2}\,\underline{\,\,\,\,\,\,\,\,\,}\,\dfrac{3}{4}$, true?

14. Which of the following will make the statement, $\dfrac{16}{20}\,\underline{\,\,\,\,\,\,\,\,\,}\,\dfrac{3}{5}$, true?

15. Which of the following will make the statement, $\dfrac{2}{20}\,\underline{\,\,\,\,\,\,\,\,\,}\,\dfrac{1}{10}$, true?

16. Which of the following will make the statement, $\dfrac{20}{50}\,\underline{\,\,\,\,\,\,\,\,\,}\,\dfrac{1}{25}$, true?

17. Erick has $\dfrac{2}{5}$ of an orange and $\dfrac{3}{10}$ of an apple. Which type of fruit does he have the most?

18. Mohamed is supposed to read $\dfrac{3}{4}$ of history and $\dfrac{1}{3}$ of science chapters in a day. Which chapter does he read the most?

19. The teacher is dividing a bag of tennis balls to give his students. He gives $\dfrac{2}{9}$ of the balls to Mary, $\dfrac{1}{3}$ to Harish, $\dfrac{7}{27}$ to James, and keeps $\dfrac{5}{27}$ to himself. Who among them has the least number of balls?

20. The teacher is dividing a bag of tennis balls to give his students. He gives $\dfrac{2}{9}$ of the balls to Mary, $\dfrac{1}{3}$ to Harish, $\dfrac{7}{27}$ to James, and keeps $\dfrac{5}{27}$ to himself. Who among them has the largest number of balls?

21. Dustin and Brian have completed $\dfrac{7}{11}$ and $\dfrac{5}{8}$ of their homework, respectively. Who has completed less homework?

22. Last week, Pedro listened to $\dfrac{2}{3}$ of his favorite music while Adam listened to $\dfrac{3}{8}$ of his favorite songs. Who listened to a bigger fraction of his favorite music?


 

Page | Next Lesson