Complex Fractions – Explanation & Examples

A fraction is made up of two parts: a numerator and a denominator; the number above the line is the numerator and the number below the line is the denominator. The line or slash in that separates the numerator and the denominator in a fraction represents division. It is used to represent how many parts we have out of the total number of parts.

The types of numerator and denominator determines the type of fraction. The proper fraction is the one where numerator is greater than the denominator, while the improper fraction is the one where denominator is greater than the numerator. There is another type of fraction called Complex Fraction, which we will see below.

What is a Complex Fraction?

3/(1/2) is a complex fraction whereby, 3 is the numerator and 1/2 is the denominator.

(3/7)/9 is also a complex fraction with 3/7 and 9 as the numerator and denominator respectively.

(3/4)/(9/10)  is another complex fraction with 3/4 as the numerator and 9/10 as the denominator.

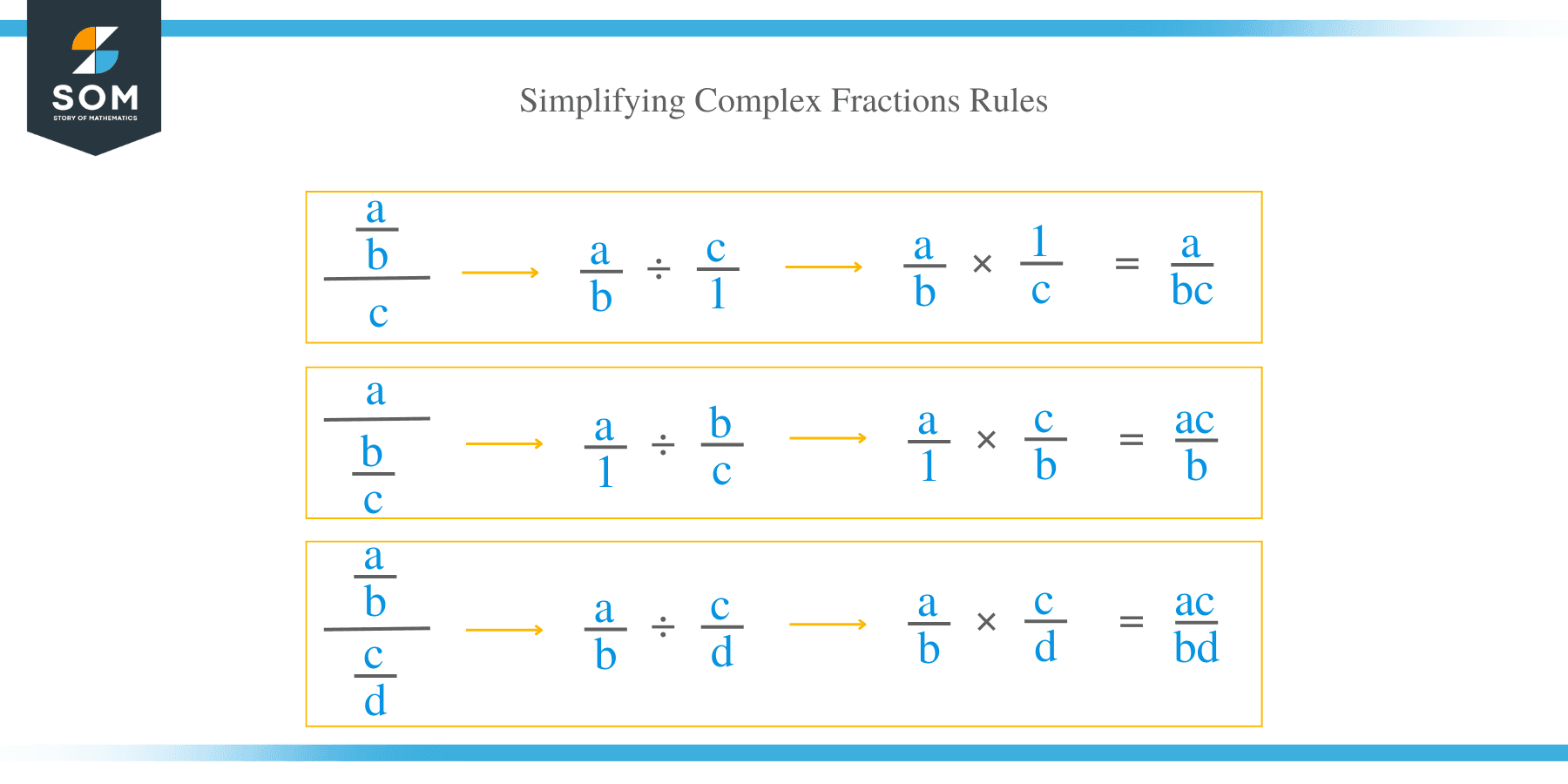
How to Simplify Complex Fractions?

There are two methods used to simplify complex fractions.

Let’s look at some of the key steps for each simplification method:

Method 1

In this method of simplifying complex fractions, the following are the procedures:

• Generate a single fraction both in the denominator and the numerator.
• Employ the division rule by multiplying the top of the fraction by the reciprocal of the bottom.
• Simplify the fraction its lowest terms possible.

Method 2

This is the easiest method of simplifying complex fractions. Here are the steps for this method:

• Start by finding the Least Common Multiple of al the denominator in the complex fractions,
• Multiply the both the numerator and denominator of the complex fraction by this L.C.M.
• Simplify the result to the lowest terms possible.

Example 1

Kelvin cuts 3/4 meters of a wire into smaller pieces. If each piece of the wire is 1/12 meters, how many pieces of the wire can Kelvin cut?

Solution

Length of each wire = 1/12 meters

Given:

The larger wire will be cut into 1/12-meter wires.

Then, the total length of a wire is 3/4 meters.

The number of pieces that can be cut:

=  (3/4) / (1/12)

The above expression is a complex fraction, therefore, change the division as multiplication and take reciprocal of the fraction in denominator.

=  3/4 x 12/1

Simplify.

=  (3 x 12) / (4 x 1)

=  (3 x 3) / (1 x 1)

=  9 / 1

=  9

So, Kelvin cut 9 pieces of the wire.

Example 2

A chicken feeder can hold 9/10 of a cup of grains. If the feeder is being filled by scoop that only holds 3/10 of a cup of grains. How many cups scoops can fill the chicken feeder?

Solution

Capacity of the chicken feeder = 9/10 of a cup of grains

Given that 3/10 of a cup grains fills the feeder, therefore the number of scoops can be found by dividing 9/10 by 3/10.

Analysis of this question results in complex fractions:

(9/10)/(3/10)

The problem is solved by finding the reciprocal of the denominator, and in this case, it is 3/10.

= 9/10 x 10/3

Simplify.

=  (9 x 10) / (10 x 3)

=  (3 x 1) / (1 x 1)

=  3 / 1

=  3

Thus the total number of scoops = 3

Example 3

A bakery uses 1/6 of a bag of baking flour in a batch of cakes. The bakery used 1/2 of a bag of baking flour on a certain day. Calculate the batches of cakes manufactured by the bakery on that day.

Solution

Amount of baking floor used to make a batch of cakes = 1/6 of a bag

If the bakery utilized 1/2 of a bag of baking flour on that day.

Then, the number of batches of cakes produced by the bakery on the day.

=  (1/2) / (1/6)

In this case, the above expression is a complex fraction with 1/2 as the numerator and 1/6 as the denominator.

Therefore, take the reciprocal of the denominator

=  1/2 x 6/1

Simplify.

=  (1 x 6) / (2 x 1)

=  (1 x 3) / (1 x 1)

=  3 / 1

=  3

Thus, the number of batches of cakes manufactured by the bakery = 3

Example 4

Simplify the complex fraction: (2 ¹/₄)/(3 ³/₅)

Solution

Start by converting the top and bottom into improper fractions:

2 ¹/₄ = 9/4

3 ³/₅ = 18/5

Therefore, we have:

(9/4)/(18/5)

Find the reciprocal of the denominator and change the operator:

9/4 x 5/18

Multiply the numerators and denominators separately:

=45/72

The numerator and denominator of the fraction have a common factor number 9, simplify the fraction to the lowest terms possible.

45/72 = 5/8

The answer = 58.

Example 5

Calculate the possible value of x in the following complex fraction.

(x/10)/(4/x) = 8/5

Solution

Start by multiplying the numerator of the complex fraction by the reciprocal of its denominator.

 x/10 * x/4 = x ²/240

Now, we have our equation as:

X ²/240=85

Multiply both sides by 40 to get:

X ²= 64

Thus, by finding the square root of both sides, you get:

X = ± 8

Therefore – 8 is the only possible value of the complex fraction.